• ロジスティック回帰式
• ロジスティック回帰の曲線例
• Logistic Regression – Leader Test
• ロジスティック回帰の曲線例

ロジスティック回帰の曲線例

• ロジスティック回帰の曲線例
• ロジスティック回帰-効果量
• ロジスティック回帰の前提

ロジスティック回帰は1+予測変数から
二値変数を予測する手法である。例：2015年の年齢で、2020年までに死亡する確率はどのくらいか？ この分析は、バイナリ・ロジスティック回帰、または単に「ロジスティック回帰」としても知られています。 関連するテクニックは、3つ以上のカテゴリーを持つ結果変数を予測する多項ロジスティック回帰です。

ロジスティック回帰 – 単純な例

ある老人ホームが、N = 284人のクライアントの性別、2015年1月1日の年齢、クライアントが2020年1月1日までに他界したかどうかに関するデータを持っています。

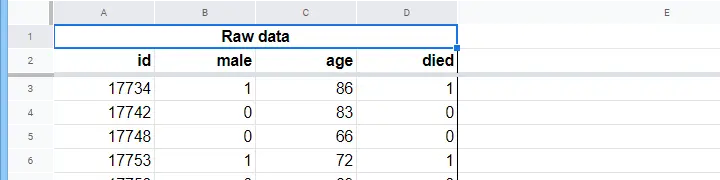
まず、年齢に注目してみましょう。 また、どの程度まで予測できるのでしょうか？

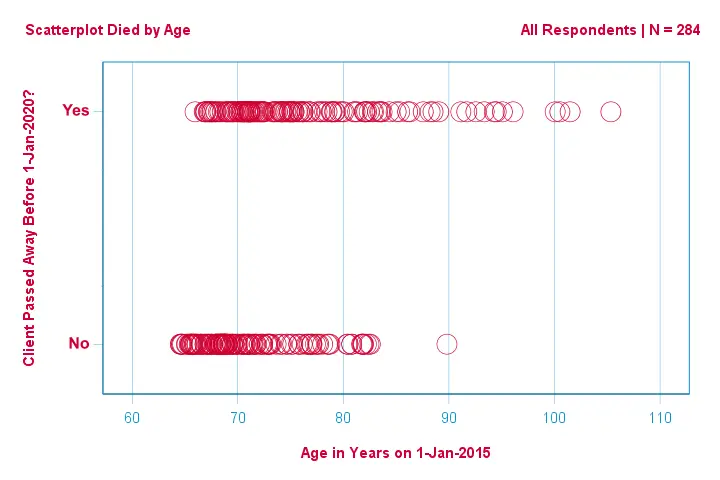
この散布図でわかることは、

• 83歳以上の顧客1人を除いて、全員が今後5年以内に死亡していること、
• 年齢の標準偏差は、生存した顧客よりも死亡した顧客で非常に大きいこと、
• 特に死亡した顧客では年齢はかなりの正の歪度を持つこと、などです。

しかし、年齢から、あるクライアントが死亡したかどうかを予測するにはどうしたらよいのでしょうか。 それは、ロジスティック曲線をあてはめることで行います。

単純ロジスティック回帰式

単純ロジスティック回帰は、1つの予測変数が与えられたときのある結果の確率を

$P(Y_i) = \frac{1}{1 + e^{3} で計算する。-\ここで、

• (P(Y_i)\) はcase \(i) に対して(Y)が真である予測確率である。
• (e} は数学的定数でおおよそ2。72;
• \(b_0) is a constant estimated from the data;
• \(b_1) is a b-coefficient estimated from the data;
• \(X_i) is the observed score on variable \(X) for case ✞(i).これはデータから推定された定数です。

ロジスティック回帰の真髄は” \(b_0}, \(b_1}) “を推定することです。 この2つの数値により、観察された任意の年齢で顧客が死亡する確率を計算することができる。 先ほどの散布図に追加した曲線の例で説明します。

Logistic Regression Example Curves

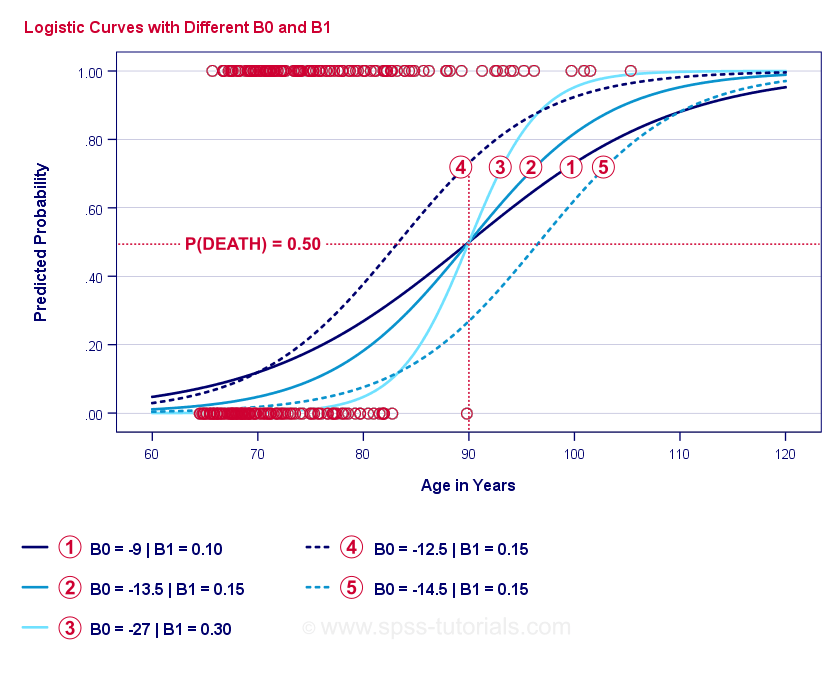
If you take a minute to compare these curves, you may see the following:

• \(b_0**) determines the horizontal position of the curves: as \(b_0**) increases, the curves shift towards the left but their steepness is unaffected. これは、曲線、、に見られる。 また、これらの曲線で は、閾値は異なるが閾値は同じであることに注意してください。
• Ⓐが大きくなると、予測される確率も大きくなり、年齢が90歳の場合、曲線はおよそ0.75の確率で死ぬと予測されます。 カーブとは、90歳でだいたい0.50と0.25の確率で死ぬと予測しています。 この関係は, Ⓐが大きくなるほど強くなる。 このことは、曲線、、を見れば明らかである。(b_1)が大きくなると、曲線は急峻になり、死亡する確率は年齢が上がるにつれて早くなる。

ここまでで、1つの疑問が残りました。 当然ながら、この確率は実際にその事象が発生した場合は高くなり、逆に発生しない場合は低くなります。 あるモデルが全回答者に対してどの程度のパフォーマンスを示すかを要約する1つの方法は、対数尤度 \(LL):

$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i)) $$

where

• (Y_i) is 1 if the event occurred and if it didn’t;
• \(ln) representing natural logarithm: what power must raise \(e) to obtain a given number?

(LL) は goodness-of-fit measure で、all else equal, ロジスティック回帰モデルは \(LL) が大きいほどデータによくフィットすることを示します。 少し分かりにくいのですが、閾値は常に負です。 そのため、
LLTができるだけゼロに近くなるような閾値を求めます。

Maximum Likelihood Estimation

線形回帰と異なり、ロジスティック回帰では閾値を簡単に計算することができません。 その代わりに、これ以上 \(LL) が増えないようになるまで、いろいろな数値を試してみる必要があります。 このような試行錯誤をイテレーションと呼びます。 このような繰り返しの中で最適な値を求めることを最尤推定といいます。 幸いなことに、これらのソフトは驚くほど優秀です。 しかし、これらのパッケージは、 \(-2LL**) を報告します。”badness-of-fit” 指標で、
カイ二乗分布に従います。 \8248>

脚注によると、最尤推定では、最適なb係数であるⒶ(b_0 )とⒷ(b_1 )を求めるのに5回の繰り返しで済むことがわかります。

Logistic Regression – B-Coefficients

ロジスティック回帰分析で最も重要な出力は、B係数です。 下の図は、私たちの例題のデータについて、それらを示しています。

詳細に入る前に、この出力は

我々のモデルを構成するb係数、
これらのb係数の標準誤差、
カイ二乗分布に従うWald統計- \((\frac{B}{SE})^2 )として計算-を簡単に示しています。
Wald統計量の自由度;
b-係数の有意水準;
指数化b-係数、または \(e^B**) は予測因子得点の変化と関連したオッズ比;
指数化b-係数の95%信頼区間です。

b-係数を用いてロジスティック回帰モデルを完成させると、

$P(death_i) = \frac{1}{1 + e^{arette,-arette,(-9.079, +arette,0.124, \cdot, age_i)}}$

75歳の顧客が5年以内に死亡する確率は

$P(death_i) = \frac{1}{1 + e^{3, -}, (-9.079,+3,0.124***, \cdot***, 75)}}=$$

$P(death_i) = \frac{1}{1 + e^{,-3,0.249}}=$

$P(death_i) = \frac{1}{1 + 0.0.780}=$

$P(death_i) \approx 0.562$

これで、誰かの年齢から5年以内の死亡を予測する方法がわかりましたね。 しかし、この予測はどの程度良いのでしょうか？ いくつかのアプローチがあります。

ロジスティック回帰 – ベースラインモデル

他の情報がない場合、どのように死亡者を予測できるのでしょうか。 さて、サンプルの50.7％が亡くなりました。

分類の目的では、通常、p（イベント）≥0.50の場合、イベントが発生すると予測します。 全員に対してp(died)=0.507なので、単純に「全員が亡くなった」と予測します。 この予測は，サンプルの50.7%が死亡した場合，正しいことになります。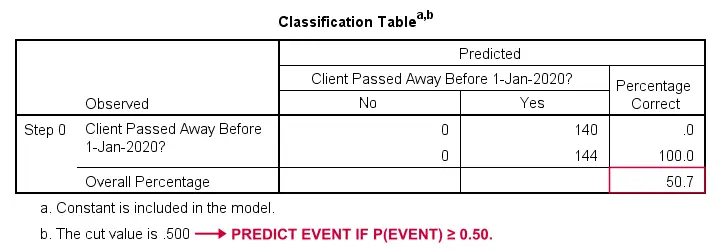

ロジスティック回帰 – 尤度比

さて、これらの予測確率と観察結果から、我々の適合度指標を計算できます：-2LL = 393.65。 我々の実際のモデル（年齢による死亡を予測する）は、-2LL = 354.20となります。 この差は尤度比(LR)と呼ばれるものです。

$LR = (-2LL_{baseline}) – (-2LL_{model})$$

重要なのは、(LR)はカイ二乗分布で、自由度¢(dfxx)に従っていることです。 df = k_{model} – k_{baseline}$$

ここで、 \(kxx) はモデルで推定されたパラメータ数を表します。 このGooglesheetに示されているように、 \(LR) and \(df) はモデル全体に対する有意水準になります。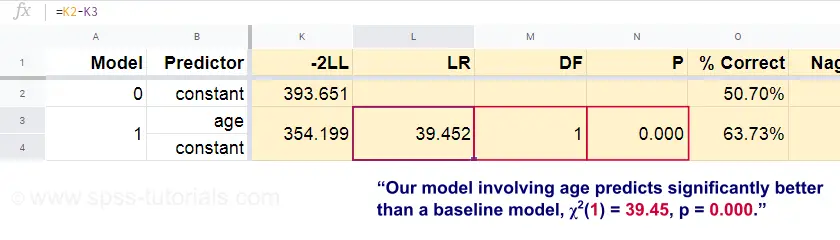

ここで帰無仮説とは、ある母集団においてあるモデルがベースラインモデルと同等に悪い予測をしているということです。 p = 0.000なので、これを棄却する。我々のモデル（年齢による死亡を予測する）は、予測変数なしのベースラインモデルよりも有意に良いパフォーマンスを示す。

Logistic Regression – Model Effect Size

我々のモデルがどれだけうまく機能しているかを評価する良い方法は、効果量測定からである。 その1つがCox & Snell R2、もしくは、 \(R^2_{CS}}) で、

$R^2_{CS} = 1 – e^{{frac{(-2LL_{model})\,-ii,(-2LL_{baseline})}{n}$

悲しいことに、( R^2_{CS} )は理論上の最大の1には決して達しないのです。 R^2_{N} = \frac{R^2_{CS}}{1 – e^{-auth{-2LL_{baseline}}{n}}$

この例では、効果量は0.130で中程度と考えられます。 \(R^2_{N}}) = 0.173で、中程度よりやや大きめです。 しかし、同じ役割を果たそうとするものです。

ロジスティック回帰 – 予測変数の効果量

奇妙なことに、個々の予測変数の効果量について言及している教科書は非常に少ないです。 おそらく、これらは SPSS に全く存在しないからでしょう。 我々がそれらを必要とする理由は、b-係数が我々の予測変数の（任意の）スケールに依存するからです：我々が年齢を年ではなく日で入力した場合、そのb-係数は非常に小さくなります。 これは明らかに、b-係数を異なるモデル内、または異なるモデル間で予測変数を比較するのに不向きです。
JASPは部分的に標準化されたb-係数を含みます： 量的予測変数（結果変数ではない）が、以下に示すようにzスコアとして入力されています。

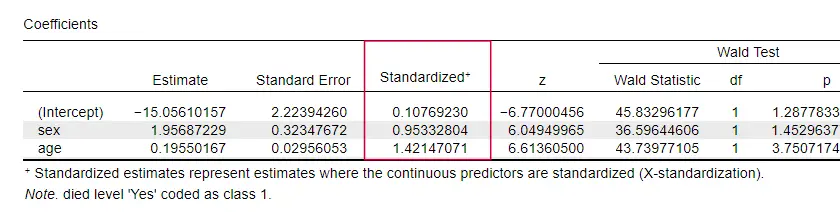
Logistic Regression Assumptions

Logistic Regression analysis requires the following assumptions:

1. independent observations;
2. correct model specification;
3. errorless measurement of outcome variable and all predictors;
4. linearity: each predictor is relatedly to \(e^B appendix) (the odds ratio.)（予測変数がオッズ比に直線的な関係がある）.

仮定4はやや議論の余地があり、多くの教科書で省略されています1,6。 これはFieldが議論しているBox-Tidwell検定で評価できる4。 これは基本的には、各予測変数とその自然対数または \(LN) との間に交互作用があるかどうかを検定することになります。

Multiple Logistic Regression

ここまでは、予測変数1つだけを使った単純ロジスティック回帰の話に限定されました。 このモデルは簡単に予測変数が追加でき、多重ロジスティック回帰になります：

$P(Y_i) = \frac{1}{1 + e^{},-},(b_0,+},b_1X_{1i}+},b_2X_{2i}+}, ….+,b_kX_{ki})}}$$where

• ○(P(Y_i)○) is the predicted probability that \(Y} is true for case \(i);
• ○(e)is a mathematical constant of roughly 2.X {(Y) }} $$$

  ここで、(P(Y_i)○は、(Inthesis)ケースに対して(Yinthesis)が真である予測確率、(e○は、凡そ2の数学定数)。72;

• \(b_0) is a constant estimated from the data;
• \(b_1), \(b_2), …. ,\(b_k) are the b-coefficient for predictors 1, 2, …. ,ⅳ(k);
• ⅳ(X_{1i}), \(X_{2i}), …。 , ⅳ(X_{ki}) is observed scores on predictors ⅳ(X_1}), ⅳ(X_2}), …予測変数に関する観測値。 ,\(X_k}) for case \(i).

Multiple Logistic Regressionでは、モデルの選択や多重共線性のチェックがよく行われます。 それ以外は単純なロジスティック回帰の延長線上にあります。

今回の基本的な紹介はロジスティック回帰のエッセンスにとどまりました。 もっと学びたい方は、省略したトピックを読むとよいでしょう。

1. odds ratio -computed as \(e^B} in logistic regression- express how probabilities change depending on predictor scores;
2. the Box-Tidwell test examine if the relations between the mentioned odds ratios and predictor scores are linear;
3. the Hosmer and Lemeshow test is an alternative goodness of fit for the entire logistic regression model.

お読みいただきありがとうございました！

1. Warner, R.M. (2013). 応用統計学（第2版）. Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). 統計学. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006).（英語）. 多変量データ解析. ニュージャージー州 Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). 心理学のための統計手法（第5版）. Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). 社会科学のための応用多変量統計学(第6版). New York: Routledge.

.