はじめに
決定木は教師あり学習アルゴリズムの一種で、回帰と分類問題の両方で使用することができます。 8031>
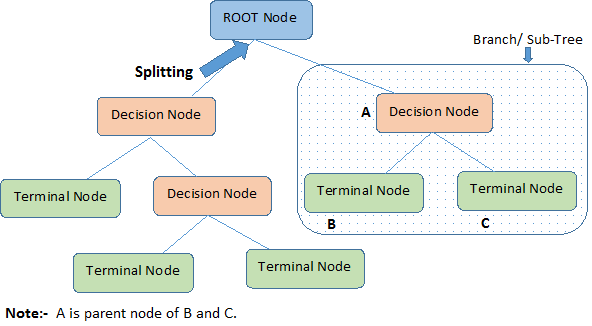
上の画像を見て、決定木の重要な用語を識別しましょう:
-
ルート ノードは全体の人口またはサンプルを表します。 8031>
-
分割は、ノードを 2 つ以上のサブノードに分割するプロセスです。
-
サブノードがさらにサブノードに分割されると、それは決定ノードと呼ばれるようになります。
-
分割しないノードは終端ノードまたは葉と呼ばれます。
-
決定ノードのサブノードを削除するとき、このプロセスは刈り込みと呼ばれています。
-
木全体の一部分を枝と呼ぶ。
-
サブノードに分けられたノードをサブノードの親ノードと呼び、一方サブノードは親ノードの子と呼ばれる。
決定木の種類
回帰木
回帰木が行う分割の性質を視覚化するために、次の画像を見てみましょう。 これは、刈り込まれていない木と、ランダムなデータセットにフィットした回帰木を示しています。 どちらの画像も、木の頂点から始まる一連の分割ルールを示している。 領域のすべての分割が、特徴の軸の1つに整列していることに注目。 軸平行分割の概念は、2次元以上の次元に簡単に一般化される。 8031>
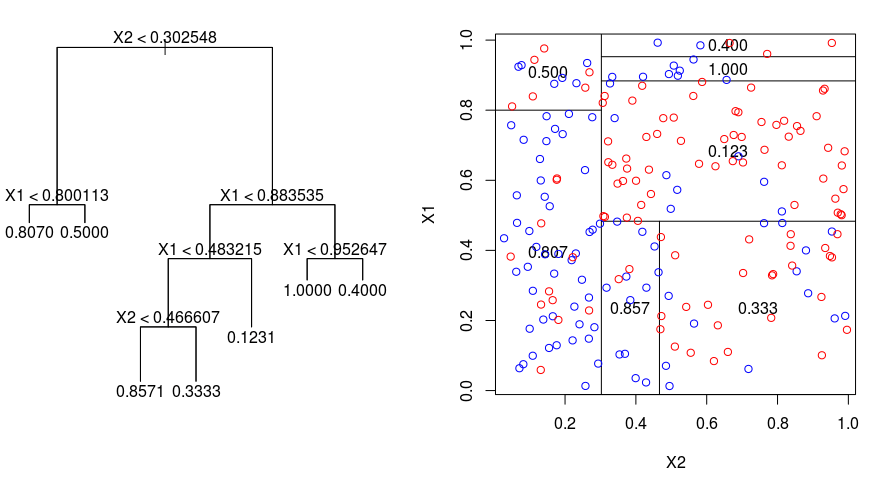
回帰木を作るには、まず再帰的バイナリ分割を使って、学習データ上で大きな木を育て、各末端ノードがある最小数の観測値より少なくなったときだけ停止させる。 再帰的バイナリ分割は、線形回帰の設定でも使用される誤差指標であるRSS(Residual Sum of Squares)を最小化するために使用される貪欲でトップダウンなアルゴリズムです。 M個のパーティションで分割された特徴空間の場合の RSS は、次のように与えられる:
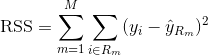
木の頂点から始めて、それを2つの枝に分割し、2空間のパーティションを作成する。
次に、この大きな木に対して、コスト複雑度刈り込みを行い、$α$の関数として、最適な部分木の列を得る。 基本的な考え方は、木の深さと学習データへの適合度のバランスをとるために、$αalpha$と呼ばれる調整パラメータを追加導入することです。 この手法は、単純に学習観測値をK倍に分割して、部分木のテスト誤差を推定するものです。
分類木
分類木は回帰木に非常に似ているが、定量的な応答ではなく、定性的な応答を予測するために使われる点が異なる。
回帰木では、あるオブザベーションに対する予測応答は同じターミナルノードに属する学習オブザベーションの平均応答で与えられることを覚えておこう。
分類木の結果を解釈する際、特定のターミナルノード領域に対応するクラス予測だけでなく、その領域に入るトレーニング観測の中のクラス比率に興味を持つことが多い。
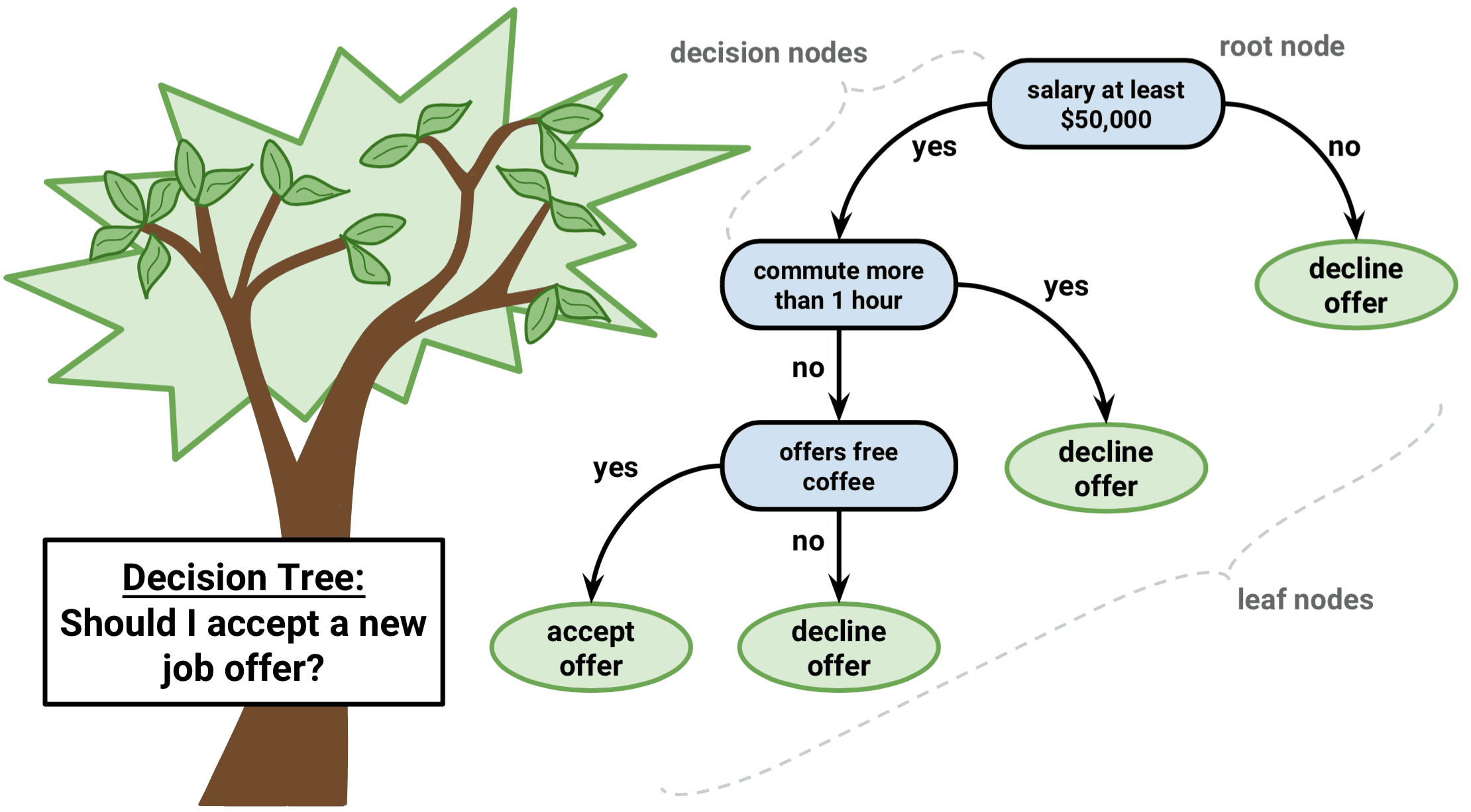
分類木を育てるタスクは回帰木を育てるタスクと非常に似ている。 回帰の設定と同じように、分類木を成長させるために再帰的なバイナリ分割を使用します。 しかし、分類の設定では、二項分割を行うための基準として二乗残差和を使用することはできません。 代わりに、以下の3つの方法のいずれかを使用できます。
- 分類誤り率。 回帰設定のように数値応答が平均値からどれだけ離れているかを見るのではなく、代わりに最も広く出現するクラスに属さない特定の領域でのトレーニング・オブザベーションの割合として「ヒット率」を定義することができる。 誤差は次の式で与えられる:
E = 1 – argmaxc($hat{pi}_{mc}$)
ここで $hat{pi}_{mc}$ は領域Rmのクラスcに属する学習データの分数を表す。 ジニ指数は代替誤差指標で、地域がどの程度「純粋」かを示すように設計されている。 この場合の “純粋さ “とは、特定のリージョン内の学習データが、どれだけ単一のクラスに属しているかを意味する。 もし地域Rmがほとんど1つのクラスcからのデータを含むなら、ジニ指数値は小さくなる:
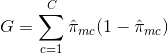
- Cross-Entropy.Gini Indexは、地域Rmがどの程度純粋かを示す代替指標である。 ジニ指数に似た第三の選択肢は、クロスエントロピーまたはデビアンスとして知られています:
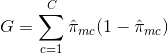
クロスエントロピーは、$hat{}_pi}_{mc}$のすべてが0または1に近い場合は、ゼロに近い値を取ることになります。 したがって、ジニ指数と同様に、m番目のノードが純粋であれば、クロスエントロピーは小さな値をとります。 実際、ジニ指数とクロスエントロピーは数値的に非常によく似ていることがわかります。
分類木を構築するとき、ジニ指数とクロスエントロピーのどちらかは、分類誤り率よりもノードの純度に敏感なので、特定の分割の品質を評価するために一般的に使われます。 8031>
決定木の利点と欠点
決定木を使用する主な利点は、直感的に非常に説明しやすいことである。 他の回帰や分類のアプローチと比較して、人間の意思決定に近いミラーリングを行います。 グラフィカルに表示することができ、ダミー変数を作成する必要なく、定性的な予測変数を簡単に処理できます。
しかしながら、決定木はかなり堅牢ではないので、一般的に他のアプローチと同じレベルの予測精度を持ちません。 8031>
多くの決定木を集約し、バギング、ランダムフォレスト、ブースティングなどの方法を使用することで、決定木の予測性能を大幅に向上させることができる。
Tree-Based Methods
Bagging
上述の決定木は高い分散に苦しんでいます。つまり、学習データをランダムに 2 分割し、両半分に決定木をあてはめると、得られる結果はかなり異なる可能性があるということです。
バギング(ブートストラップ集計)は、同じデータセットの異なるサブサンプルでモデル化した複数の分類器の結果を組み合わせることにより、予測値の分散を減らすために使用するテクニックです。 以下はバギングの式です:

この式では、$B$個の異なるブートストラップ学習データセットを生成します。 そして、$b$番目のブートストラップされた学習セットでメソッドを学習して、$hat{f}_{b}(x)$を取得し、最後に予測値を平均化する。
以下の図は、バギングにおける3つのステップを示している:
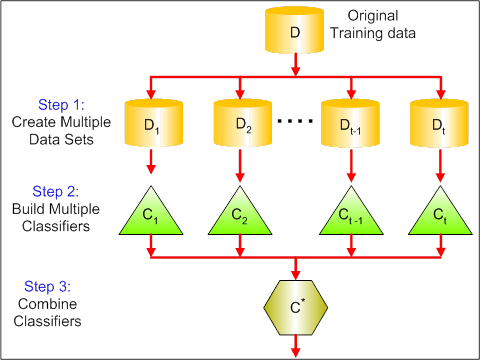
-
ステップ1:ここでは、元のデータを新しいデータで置き換えます。 新しいデータは通常、元のデータの列と行の一部を持っており、それをバギングモデルのハイパーパラメータとして使用することができます。
-
ステップ3:最後に、問題に応じて、すべての分類器の予測を組み合わせるために、平均値を使用します。 一般に、これらの結合値は単一のモデルよりも堅牢です。
バギングにより、多くの回帰および分類メソッドの予測を改善できますが、決定木に特に有用です。 回帰/分類木にバギングを適用するには、単に $B$ ブートストラップされた学習セットを使用して $B$ 回帰/分類木を構築し、結果の予測値を平均化します。 これらの木は深く成長し、刈り込まれることはありません。 したがって、個々の木は高い分散を持ちますが、バイアスは低くなります。 8031>
Bagging は大まかに言って、数百または数千の木を 1 つの手順にまとめることで、精度を大幅に向上させることが実証されている。
Random Forests
Random Forests は回帰と分類のタスクを実行できる多目的の機械学習方法である。 また、次元削減法、欠損値、異常値、およびデータ探索の他の重要なステップを引き受け、かなり良い仕事をします。
Random Forests は、木を装飾する小さな調整によって、袋小路木に対する改良を提供します。 バギングと同様に、ブートストラップされたトレーニング サンプルで多数の決定木を構築します。 しかし,これらの決定木を構築するとき,木における分割が検討されるたびに,$p$個の予測変数の全セットから,分割候補としてm個の予測変数の無作為標本が選択される. その分割は、それらの$m$個の予測変数のうち1つだけを使用することが許される。
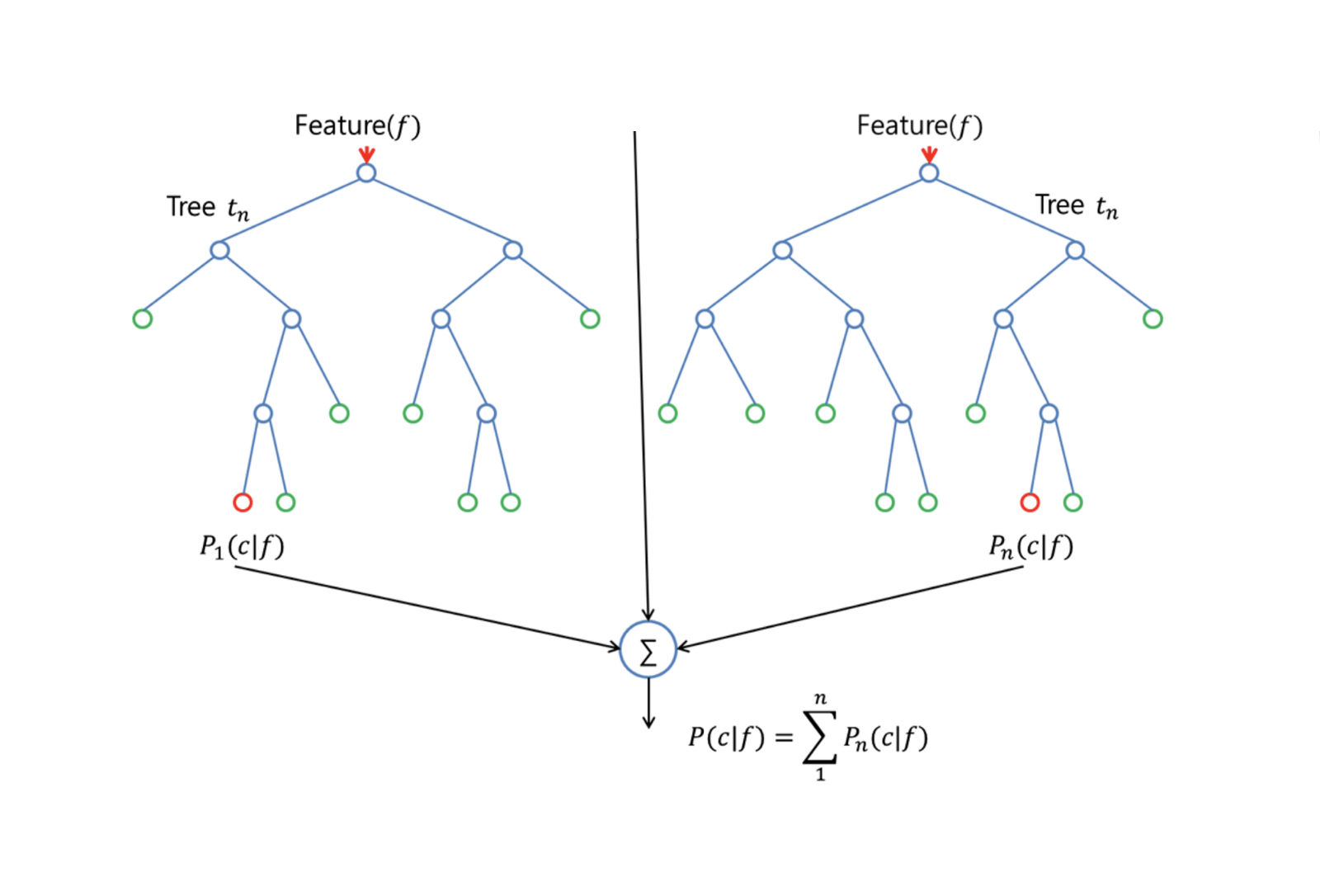
ランダムフォレストを成長させるためには、次のようにします:
-
まず、学習セット内のケース数をKとします。 そして、このK件の中からランダムにサンプルを取り、このサンプルを学習セットとして木を育てる。
-
入力変数が$p$ある場合、各ノードで$p$から$m$個のランダム変数を選択できるように、数$m < p$を指定する。 8031>
-
各木はその後、可能な限り大きくなり、枝刈りは必要ない。
-
最後に、対象の木の予測を集約して新しいデータを予測する。
ランダム・フォレストは欠損データの推定に非常に有効で、データの大きな割合が欠損した場合でも精度を維持することができる。 また、クラスが不均衡なデータセットにおける誤差のバランスをとることができます。 最も重要なことは、次元の大きい巨大なデータセットを扱うことができることです。 しかし、ランダムフォレストを使用することの欠点は、特に回帰を行う場合、ノイズの多いデータセットを簡単にオーバーフィットする可能性があることです。
Boosting
ブーストは決定木から得られる予測を改善する別のアプローチです。 バギングやランダムフォレストと同様に、回帰や分類のための多くの統計的学習法に適用できる一般的なアプローチである。 バギングでは、ブートストラップを用いて元の学習データセットのコピーを複数作成し、それぞれのコピーに別々の決定木をフィットさせ、その後、単一の予測モデルを作成するためにすべての木を結合することを思い出します。 注目すべきは、各木が他の木から独立して、ブートストラップされたデータセットで構築されることです。
Boosting は、木が連続して成長することを除いて、同様の方法で動作します。 ブーストはブートストラップ・サンプリングを使用せず、各木は元のデータセットの修正バージョンにフィットさせる。

回帰木と分類木の両方で、ブースティングは次のように動作します。
-
データに単一の大きな決定木をフィットすることとは異なり、これはデータをハード フィットしオーバー フィットの可能性がありますが、代わりにブーストのアプローチはゆっくりと学習してゆきます。 8031>
-
そして、残差を更新するために、この新しい決定木をフィットした関数に追加する。 これらの木はそれぞれ、アルゴリズムのパラメータ$d$で決まる数個の終端ノードを持つ、かなり小さなものにすることができる。
-
縮小パラメータ$nu$は処理をさらに遅くし、より多くの異なる形の木が残差を攻撃することを可能にします。 ブースティングは、リスク分析、感情分析、予測広告、価格モデリング、売上予測、患者診断など、多くの難しい分類や回帰の問題を解決するために使用されています。
Decision Trees in R
分類木
この部分では、Rの
treeパッケージを使用してCarseatsデータセットを扱いますが、最初にISLRとtreeパッケージをR Studio環境にインストールしておく必要があることに注意して下さい。 まず、ISLRパッケージからCarseatsデータフレームをロードします。library(ISLR)data(package="ISLR")carseats<-Carseatstreeパッケージもロードしましょう。require(tree)この
Carseatsデータセットは、以下の11変数について400の観測値を持つデータフレームです:-
Sales: unit sales in thousands
-
CompPrice: 8031>
-
Income: コミュニティーの所得水準(1000ドル単位)
-
Advertising:
-
Population: local ad budget at each location in thousands
-
Price: price for car seats at each site
-
ShelveLoc.JPは、地域の人口(千人単位)。 Bad, Good, Mediumはシェルビングロケーションの品質を示す
-
Age: 人々の年齢レベル
-
Education: 場所でのEDレベル
-
Urban: 都会的。 Yes/No
-
US: Yes/No
names(carseats)Let’s look at the histogram of car sales:
hist(carseats$Sales)Observe that
Salesis a quantitative variable. あなたは、二値応答を持つ木を使って実証したい。 そのためには、Salesをバイナリ変数にして、Highという変数にします。 売上が8より小さければ、高くないということになる。 そうでなければ、高くなります。 8031>High = ifelse(carseats$Sales<=8, "No", "Yes")carseats = data.frame(carseats, High)さて、決定木を使ったモデルを埋めてみましょう。 もちろん、応答変数
HighはSalesから作られたものなので、ここでSalesの変数を持つことはできません。tree.carseats = tree(High~.-Sales, data=carseats)分類木のサマリーを見てみましょう。
summary(tree.carseats)関係する変数、終端ノード数、残留平均偏差、そして誤分類エラー率を見ることができます。 より視覚的にするために、木もプロットして、便利な
text関数を使って注釈を付けてみましょう:plot(tree.carseats)text(tree.carseats, pretty = 0)非常に多くの変数があり、木を見るのが非常に複雑になっています。 少なくとも、それぞれの終端ノードで、
YesまたはNoとラベル付けされていることはわかるだろう。 各分割ノードでは、変数と分割選択の値が表示されている(例えば、Price < 92.5やAdvertising < 13.5)。木の詳細な要約は、単に印刷すればよい。 8031>
tree.carseatsそろそろツリーを刈り込んでみようか。
carseatsのデータフレームを250個のトレーニングサンプルと150個のテストサンプルに分割して、トレーニングセットとテストを作成しましょう。 まず、結果の再現性を高めるために種を設定します。 そして、サンプルのID(インデックス)番号からランダムにサンプルを取ります。 具体的には、車のシートの列数1~n列、つまり400の集合からサンプルを採取します。 8031>set.seed(101)train=sample(1:nrow(carseats), 250)で、この
trainというインデックスが得られ、これは400個のオブザベーションのうち250個をインデックスしていることになります。trainに等しいサブセットを使用するようにツリーに指示する以外は、同じ式を使って、treeでモデルを再フィットすることができます。tree.carseats = tree(High~.-Sales, carseats, subset=train)plot(tree.carseats)text(tree.carseats, pretty=0)データセットが少し違うので、プロットは少し違って見えるでしょう。
次にこの木を使って、テストセットで
predict法を使い、木を予測することにします。 ここで実際にclassラベルを予測します。tree.pred = predict(tree.carseats, carseats, type="class")次に、誤分類表を使って誤差を評価します。
with(carseats, table(tree.pred, High))対角線上は正しい分類、対角線外は誤った分類です。 正しいものだけを再集計したい。 そのためには、2つの対角線の和を合計(150のテスト観測)で割ればよい。
(72 + 43) / 150OK、この木で0.76の誤差が得られる。
大きな繁みを育てる場合、分散が多すぎる可能性もある。 したがって、クロスバリデーションを使って最適にツリーを刈り込んでみましょう。
cv.treeを使って、誤分類の誤差を基準にして刈り込みを行います。cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)cv.carseats結果をプリントアウトすると、クロスバリデーションの経路の詳細が表示されます。 8031>
これをプロットしてみましょう。
plot(cv.carseats)プロットを見ると、250のクロスバリデーションされたポイントでの誤分類エラーによって、下降スパイラル部分が見られます。 そこで、下降の段にある値(12)を選んでみましょう。 そして、その木を特定するために、木の大きさを12に刈り込んでみましょう。 8031>
prune.carseats = prune.misclass(tree.carseats, best = 12)plot(prune.carseats)text(prune.carseats, pretty=0)以前のツリーよりも少し浅くなり、実際にラベルを読むことができるようになりました。 もう一度テストデータセットで評価してみましょう。
tree.pred = predict(prune.carseats, carseats, type="class")with(carseats, table(tree.pred, High))(74 + 39) / 150正しい分類が少し落ちたようですね。 元の木とほぼ同じ結果になっているので、枝刈りをしても誤分類の誤差に関してはあまり問題にはならず、よりシンプルな木になりました。
木はあまり良い予測誤差を与えないことが多いので、予測や誤分類に関する限り、木を上回る傾向にあるランダムフォレストとブースティングを見ていきましょう。 このデータセットはMASSパッケージの中にあります。
library(MASS)data(package="MASS")boston<-Bostondim(boston)names(boston)また、
randomForestパッケージをロードしましょう。require(randomForest)ランダムフォレスト用のデータを準備するために、種を設定し、300の観測値からなるサンプル学習セットを作成しましょう。 各郊外には、一人当たりの犯罪、産業の種類、住居あたりの平均部屋数、住居の平均築年数の割合などの変数があります。 応答変数として、
medv– これらの郊外の持ち家の中央値を使いましょう。ランダムフォレストをフィットさせて、そのパフォーマンスを見ましょう。
rf.boston = randomForest(medv~., data = boston, subset = train)rf.bostonランダムフォレストをプリントアウトすると、木の本数(500本)、平均2乗残差(MSR)、説明される分散のパーセンテージが表示されます。 MSR と% variance explained は out-of-bag 推定値に基づいており、正直なエラー推定値を得るためのランダムフォレストにおける非常に賢い装置です。
ランダムフォレストにおける唯一の調整パラメータは
mtryという引数で、これは各木の分割を行うときに選択する変数の数です。 ここで見るように、mtryはBoston Housingのデータにある13個の探索変数(medvを除く)のうち4個です。つまり、ツリーがノードを分割するようになるたびに、4個の変数がランダムに選択され、その後、その4個の変数のうち1つに限定して分割が行われることになります。あなたは一連のランダムフォレストをフィットさせるつもりです。 変数が13個あるので、
mtryを1から13までとします。-
誤差を記録するために、2つの変数
oob.errとtest.errを設定します。 -
1から13までの
mtryのループで、まずtrainデータセットにその値のmtryで、木の数を350に制限してrandomForestをフィットさせるのですね。 -
そして、オブジェクトの平均二乗誤差(バッグ外誤差)を抽出する。
-
そして、
fit(randomForestのフィット)を使用してテストデータセット(boston)で予測する。 -
最後にテスト誤差を計算します。平均二乗誤差は
mean( (medv - pred) ^ 2 ).
oob.err = double(13)test.err = double(13)for(mtry in 1:13){ fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350) oob.err = fit$mse pred = predict(fit, boston) test.err = with(boston, mean( (medv-pred)^2 ))}基本的にあなたは4550本(350本の13倍)成長させただけなのです。 では、
matplotコマンドでプロットしてみましょう。 テスト誤差と袋小路外誤差を束ねて2列の行列を作ります。 行列には他にもいくつかの引数があり、プロット文字の値 (pch = 23は塗りつぶしの菱形)、色 (赤と青)、type equals both (両方の点をプロットして線で結ぶ)、Y軸の名前 (Mean Squared Error)、があります。 また、プロットの右上に凡例を置くこともできます。matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))理想的には、これら2つの曲線は並ぶはずですが、テスト誤差が少し低いような気がします。 しかし、このテスト誤差の推定値には、かなりのばらつきがあるのです。 バッグ外エラー推定値はあるデータセットで計算され、テスト エラー推定値は別のデータセットで計算されたので、これらの差は標準誤差の範囲内です。
赤いカーブが青いカーブの上に滑らかにあることに気づきましたか。 これらの誤差推定値は非常に相関があります。なぜなら、
randomForestのmtry = 4とmtry = 5は非常に似ているからです。 そのため、それぞれの曲線はかなり滑らかなものとなっています。 見えてくるのは、少なくともテスト誤差については、4前後のmtryが最も最適な選択であるように思われることです。 この袋小路外誤差のmtryの値は9.つまり、非常に少ない階層で、ランダムフォレストを使った非常に強力な予測モデルを当てはめることができたわけです。 どうでしょうか? 左側は1本の木の性能を示しています。 out-of-bagの平均二乗誤差は26ですが、約15(半分より少し上)にまで下がっていますね。 つまり、誤差が半分になったということです。 8031>
Boosting
ランダムフォレストと比較して、ブースティングはより小さく、より堅い木を育て、バイアスをかけて行く。 R.
require(gbm)GBM は、二乗誤差損失を行うので、分布はガウシアンであることを要求してきます。 GBMに1万本の木を要求することになりますが、これは多いように聞こえますが、浅い木になります。 交互作用の深さは分割の数なので、各木に4つの分割が必要です。
boost.boston = gbm(medv~., data = boston, distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)summary(boost.boston)summary関数は変数の重要度プロットを提供します。 相対的な重要度が高い変数が2つあるようです。rm(部屋数) とlstat(コミュニティ内の低経済的地位の人々の割合) です。 この2つの変数をプロットしてみましょう:plot(boost.boston,i="lstat")plot(boost.boston,i="rm")1番目のプロットは、郊外の低い地位の人々の割合が高いほど、住宅価格の値が低くなることを示しています。 2番目のプロットは、部屋数との逆の関係を示しています:価格が上昇すると、家の中の平均部屋数は増加します。
いよいよテストデータセットでブーストモデルを予測するときです。 木の数の関数としてのテストパフォーマンスを見てみましょう。
-
まず、木の数を100から10000まで100ステップのグリッドにします。
-
次に、ブーストされたモデルに対して
predict関数を実行します。 これはn.treesを引数にとり、テストデータに対する予測値の行列を生成します。 -
行列の次元は206個のテスト観測値と100種類の木の値における100種類の予測ベクトルです。
n.trees = seq(from = 100, to = 10000, by = 100)predmat = predict(boost.boston, newdata = boston, n.trees = n.trees)dim(predmat)
いよいよ各予測ベクトルに対するテスト誤差を計算します。
-
predmatは行列、medvはベクトルで、したがって (predmat–medv) は差分の行列と言えます。 この平方差の列(平均)に対してapply関数を使用することができます。 8031> -
そして、Random Forestで使ったものと同じようなパラメータを使ってプロットします。
boost.err = with(boston, apply( (predmat - medv)^2, 2, mean) )plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")abline(h = min(test.err), col = "red")
木が増えるにつれて、ブースティング誤差はかなり小さくなっていますね。 これは、ブースティングがオーバーフィッティングになりにくいことを示す証拠です。 randomForestのベストテスト誤差もプロットしてみましょう。 8031>
Conclusion
以上で、決定木モデル(分類木、ランダムフォレスト、ブースト木)の構築に関するRチュートリアルは終了です。 後者2つは、必要に応じていつでも使える強力な手法です。 私の経験では、ブースティングは通常ランダムフォレストを凌駕しますが、ランダムフォレストの方が実装が簡単です。 RandomForest では、調整パラメータは木の数だけですが、Boosting では、木の数以外にも、縮小率や相互作用の深さなど、より多くの調整パラメータが必要なのです。
-