Zákon radioaktivního rozpadu
Pokud se jednotlivé jádro přemění na jiné s emisí záření, říkáme, že se jádro rozpadá. Radioaktivní rozpad nastává u všech jader s \(Z > 82\) a také u některých nestabilních izotopů s \(Z < 83\). Rychlost rozpadu je úměrná počtu původních (nerozpadlých) jader N v látce. Počet jader ztracených rozpadem, \(-dN\) v časovém intervalu dt, se zapisuje
\
kde \(\lambda\) se nazývá rozpadová konstanta. (Znaménko minus znamená, že počet původních jader v čase klesá.) Jinými slovy, čím více jader je k dispozici pro rozpad, tím více se jich rozpadne (v čase dt). Rovnici \ref{eq2} lze přepsat jako
\
Integrujeme obě strany rovnice a definujeme \(N_0\) jako počet jader v okamžiku \(t = 0\), dostaneme
\
Tím získáme
\
Přičteme-li levou a pravou stranu rovnice \ref{eq4} jako mocninu \(e\), máme zákon radioaktivního rozpadu.
Zákon radioaktivního rozpadu
Celkový počet \(N\) radioaktivních jader zbývajících po čase \(t\) je
\
kde \(\lambda\) je rozpadová konstanta pro dané jádro.
Celkový počet jader klesá nejprve velmi rychle a pak pomaleji (obrázek \(\PageIndex{2}\))
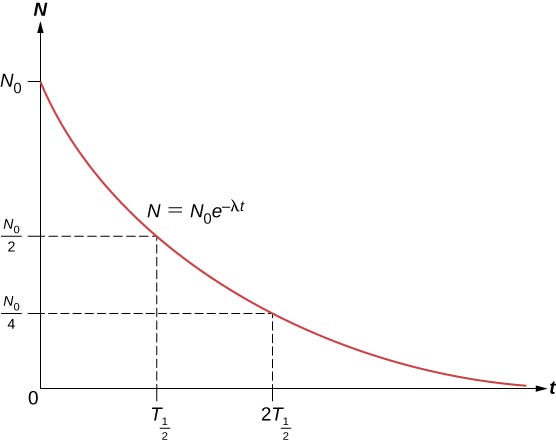
Doba poločasu rozpadu \((T_{1/2})\) radioaktivní látky je definována jako doba, za kterou se rozpadne polovina původních jader (nebo doba, za kterou zůstane polovina původních jader). Poločas rozpadu nestabilních izotopů je uveden v tabulce nuklidů. Počet radioaktivních jader zbývajících po celočíselném (n) počtu poločasů rozpadu je tedy
\
Je-li rozpadová konstanta \((\lambda)\) velká, je poločas rozpadu malý a naopak. Pro určení vztahu mezi těmito veličinami si všimněte, že když \(t = T_{1/2}\), pak \(N = N_0/2\).
Takže rovnici \ref{eq5} lze přepsat jako
\
Dělením obou stran \(N_0\) a přirozeným logaritmem získáme
\
což redukuje na
\
Takže, známe-li poločas rozpadu T1/2 radioaktivní látky, můžeme zjistit její rozpadovou konstantu. Doba života \(\overline{T}\) radioaktivní látky je definována jako průměrná doba, po kterou existuje jádro před rozpadem. Doba života látky je právě reciproká hodnota rozpadové konstanty, zapsaná jako
\
Aktivita A je definována jako velikost rychlosti rozpadu neboli
\
Infinitezimální změna dN v časovém intervalu dt je záporná, protože počet mateřských (nerozpadlých) částic klesá, takže aktivita (A) je kladná. Definujeme-li počáteční aktivitu jako \(A_0 = \lambda N_0\), máme
\
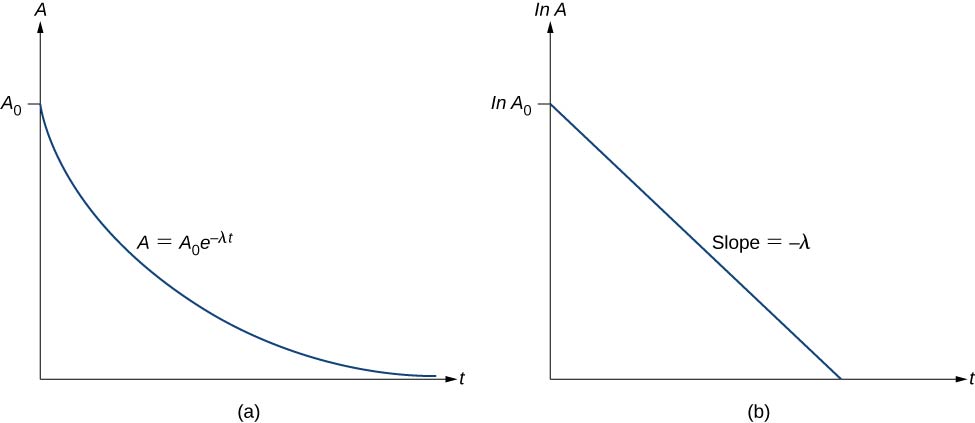
Takže aktivita A radioaktivní látky s časem exponenciálně klesá (obrázek \(\PageIndex{3}\))
Příklad \(\PageIndex{1}\): Rozpadová konstanta a aktivita stroncia-90
Rozpadový poločas stroncia-90, \(\ce{_{38}^{90}Sr}\), je 28,8 y. Určete (a) jeho rozpadovou konstantu a (b) počáteční aktivitu 1,00 g materiálu.
Strategie
Rozpadovou konstantu můžeme určit přímo z rovnice \ref{eq8}. Abychom určili aktivitu, musíme nejprve zjistit počet přítomných jader.
Řešení
a. Zjistíme, že rozpadová konstanta je
\
b. Atomová hmotnost \(_{38}^{90}Sr\) je 89,91 g. Pomocí Avogadrova čísla \(N_A = 6,022 \krát 10^{23}\) atomů/mol zjistíme počáteční počet jader v 1,00 g materiálu:
\
Z toho zjistíme, že aktivita \(A_0\) při \(t = 0\) pro 1. Rozpad \(N_A = 6,022 \krát 10^{23}\) se rovná 0,00 g materiálu.00 g stroncia-90 je
\
Vyjádříme-li \(\lambda\) ve smyslu poločasu rozpadu látky, dostaneme
\
Z toho vyplývá, že aktivita se po jednom poločasu rozpadu sníží na polovinu. Rozpadovou konstantu \(\lambda\) můžeme určit měřením aktivity v závislosti na čase. Vezmeme-li přirozený logaritmus levé a pravé strany rovnice \ref{eq11}, dostaneme
\
Tato rovnice má lineární tvar \(y = mx + b\). Vyneseme-li do grafu \ln A v závislosti na t, očekáváme přímku se sklonem \(-\lambda\) a úsečkou y \(\ln \, A_0\) (obrázek \(\PageIndex{3b}\). Aktivita A je vyjádřena v jednotkách becquerelů (Bq), kde jeden \(1 \, Bq = 1 \, rozpad \, na \, sekunda\). Tuto veličinu lze také vyjádřit v rozpadech za minutu nebo rozpadech za rok. Jednou z nejběžnějších jednotek aktivity je curie (Ci), definovaná jako aktivita 1 g \(^{226}Ra\). Vztah mezi Bq a Ci je
\
Příklad \(\PageIndex{2}\):
Přibližně \(20\%\) hmotnosti lidského těla tvoří uhlík. Vypočítejte aktivitu způsobenou \(^{14}C\) v 1,00 kg uhlíku, který se nachází v živém organismu. Vyjádřete aktivitu v jednotkách Bq a Ci.
Strategie
Aktivitu \(^{14}C\) určíme pomocí rovnice \(A_0 = \lambda N_0\), kde λ je rozpadová konstanta a \(N_0\) je počet radioaktivních jader. Počet jader \(^{14}C\) ve vzorku o hmotnosti 1,00 kg se stanoví ve dvou krocích. Nejprve určíme počet jader \(^{12}C\) pomocí pojmu mol. Za druhé tuto hodnotu vynásobíme \(1,3 \krát 10^{-12}\) (známé množství \(^{14}C\) ve vzorku uhlíku z živého organismu), abychom určili počet jader \(^{14}C\) v živém organismu. Rozpadová konstanta se určí ze známého poločasu rozpadu \(^{14}C\) (dostupného z ).
Roztok
Jeden mol uhlíku má hmotnost 12,0 g, protože je téměř čistý \(^{12}C\). Počet jader uhlíku v kilogramu je tedy
\
Počet jader \(^{14}C\) v 1 kg uhlíku je tedy
\
Nyní můžeme zjistit aktivitu \(A\) pomocí rovnice \ref{eq11}. Zadáním známých hodnot získáme
\
neboli \(7,89 \krát 10^9\) rozpadů za rok. Pro převod na jednotku Bq jednoduše převedeme roky na sekundy. Tedy
\
neboli 250 rozpadů za sekundu. Pro vyjádření A v curie použijeme definici curie,
\
Tedy,
\
Význam
Přibližně \(20\%\) hmotnosti lidského těla tvoří uhlík. V lidském těle dochází každou sekundu ke stovkám rozpadů \(^{14}C\). Uhlík-14 a další přirozeně se vyskytující radioaktivní látky v těle tvoří pozadí vystavení člověka jadernému záření. Jak uvidíme dále v této kapitole, tato úroveň aktivity je hluboko pod maximálními doporučenými dávkami.
.