• Logistická regrese – rovnice
• Logistická regrese – příklady křivek
• Logistická regrese – příklady. B-koeficienty
• Logistická regrese – velikost efektu
• Předpoklady logistické regrese

Logistická regrese je technika pro předpověď
dichotomické výsledné proměnné z 1+ prediktorů.Příklad: Jaká je pravděpodobnost, že lidé zemřou před rokem 2020, vzhledem k jejich věku v roce 2015? Všimněte si, že „zemřít“ je dichotomická proměnná, protože má pouze 2 možné výsledky (ano nebo ne).
Tato analýza je také známá jako binární logistická regrese nebo jednoduše „logistická regrese“. Příbuznou technikou je multinomiální logistická regrese, která předpovídá výsledné proměnné s více než 3 kategoriemi.

Logistická regrese – jednoduchý příklad

Domov důchodců má údaje o pohlaví N = 284 klientů, jejich věku k 1. lednu 2015 a o tom, zda klient zemřel před 1. lednem 2020. Surová data jsou v tomto Googlesheetu, částečně zobrazena níže.

Nejprve se zaměříme pouze na věk:můžeme z věku v roce 2015 předpovědět úmrtí před rokem 2020?A -pokud ano- jak přesně? A do jaké míry? Dobrým prvním krokem je prohlédnout si rozptylový graf, jako je ten, který je uveden níže.

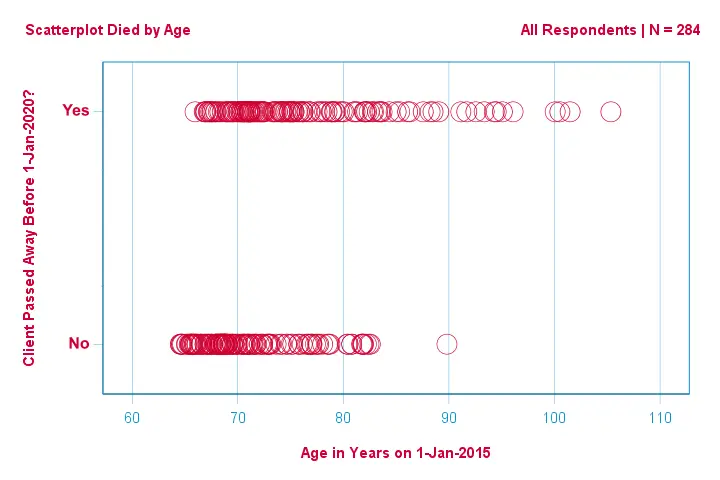
Několik věcí, které na tomto rozptylovém grafu vidíme, je, že

• všichni klienti starší 83 let kromě jednoho zemřeli během následujících 5 let;
• směrodatná odchylka věku je mnohem větší u klientů, kteří zemřeli, než u klientů, kteří přežili;
• věk má značnou kladnou šikmost, zejména u klientů, kteří zemřeli.

Jak ale můžeme předpovědět, zda klient zemřel, vzhledem k jeho věku? Uděláme to právě tak, že dosadíme logistickou křivku.

Rovnice jednoduché logistické regrese

Prostá logistická regrese počítá pravděpodobnost nějakého výsledku vzhledem k jedné prediktivní proměnné jako

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}$$

kde

• \(P(Y_i)\) je predikovaná pravděpodobnost, že \(Y\) je pravdivé pro případ \(i\);
• \(e\) je matematická konstanta přibližně 2.72;
• \(b_0\) je konstanta odhadnutá z dat;
• \(b_1\) je koeficient b odhadnutý z dat;
• \(X_i\) je pozorované skóre proměnné \(X\) pro případ \(i\).

Sama podstata logistické regrese spočívá v odhadu \(b_0\) a \(b_1\). Tato 2 čísla nám umožňují vypočítat pravděpodobnost úmrtí klienta při jakémkoli pozorovaném věku. Ilustrujeme to na několika příkladových křivkách, které jsme přidali do předchozího rozptylu.

Příkladové křivky logistické regrese

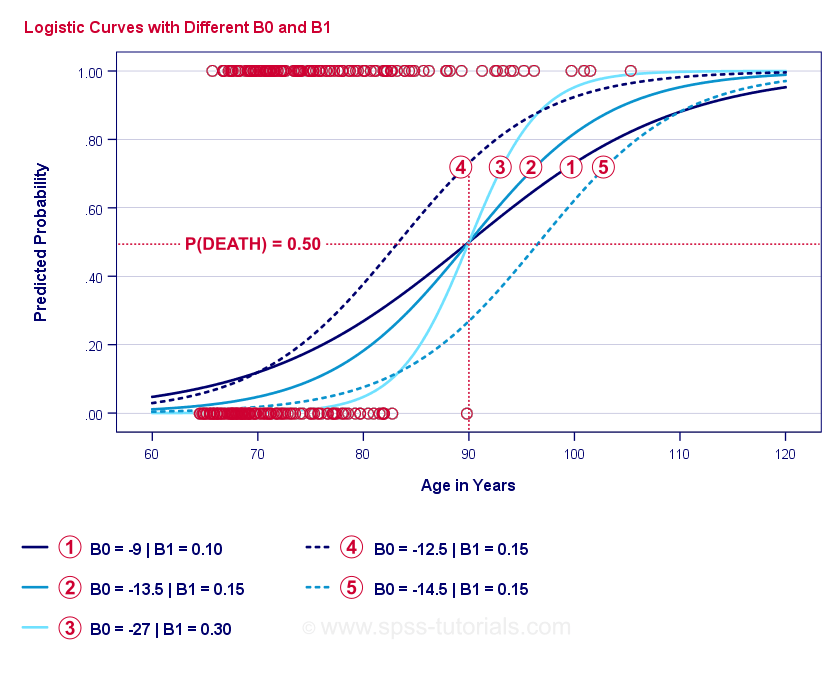
Pokud věnujete chvíli porovnání těchto křivek, můžete si všimnout následujícího:

• \(b_0\) určuje vodorovnou polohu křivek: jak \(b_0\) roste, křivky se posouvají doleva, ale jejich strmost se nemění. To je vidět u křivek , a . Všimněte si, že \(b_0\) se liší, ale \(b_1\) je pro tyto křivky stejné.
• S rostoucí hodnotou \(b_0\) rostou i předpovídané pravděpodobnosti: při věku = 90 let předpovídá křivka zhruba 0,75 pravděpodobnosti úmrtí. Křivky a předpovídají pro 90letého klienta pravděpodobnost úmrtí zhruba 0,50 a 0,25.
• \(b_1\) určuje strmost křivek: pokud \(b_1\) > 0, pravděpodobnost úmrtí se s rostoucím věkem zvyšuje. Tento vztah je tím silnější, čím je \(b_1\) větší. Křivky , a tento bod ilustrují: jak se \(b_1\) zvětšuje, křivky jsou strmější, takže pravděpodobnost úmrtí roste s rostoucím věkem rychleji.

Prozatím nám zbývá jedna otázka: Jak zjistíme „nejlepší“ \(b_0\) a \(b_1\)?

Logistická regrese – Log Likelihood

Pro každého respondenta odhaduje logistický regresní model pravděpodobnost, že nastala nějaká událost \(Y_i\). Je zřejmé, že tyto pravděpodobnosti by měly být vysoké, pokud k události skutečně došlo, a naopak. Jedním ze způsobů, jak shrnout, jak dobře funguje určitý model pro všechny respondenty, je logaritmická pravděpodobnost \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)). + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

kde

• \(Y_i\) je 1, pokud událost nastala, a 0, pokud nenastala;
• \(ln\) označuje přirozený logaritmus: na jakou mocninu musíte zvýšit \(e\), abyste dostali dané číslo?

\(LL\) je měřítkem dobré shody: při stejných ostatních podmínkách logistický regresní model vyhovuje datům lépe, pokud je \(LL\) větší. Poněkud matoucí je, že \(LL\) je vždy záporné. Chceme tedy najít hodnoty \(b_0\) a \(b_1\), pro které
\(LL\) je co nejblíže nule.

Odhad maximální věrohodnosti

Na rozdíl od lineární regrese nelze u logistické regrese snadno vypočítat optimální hodnoty pro \(b_0\) a \(b_1\). Místo toho musíme zkoušet různá čísla, dokud se \(LL\) dále nezvyšuje. Každý takový pokus se nazývá iterace. Proces hledání optimálních hodnot pomocí takových iterací je znám jako odhad maximální věrohodnosti.

Takto tedy v podstatě statistický software – například SPSS, Stata nebo SAS – získává výsledky logistické regrese. Naštěstí jsou v tom úžasně dobré. Ale místo toho, aby tyto balíky uváděly \(LL\), uvádějí \(-2LL\).\(-2LL\) je míra „špatné shody“, která se řídí rozdělením
chi-kvadrát.Díky tomu je \(-2LL\) užitečné pro porovnávání různých modelů, jak uvidíme za chvíli. Ve výstupu uvedeném níže je \(-2LL\) označeno jako -2 Log likelihood.

Poznámka pod čarou nám říká, že odhad maximální věrohodnosti potřeboval pouze 5 iterací pro nalezení optimálních b-koeficientů \(b_0\) a \(b_1\). Podívejme se tedy nyní na ně.

Logistická regrese – B-koeficienty

Nejdůležitějším výstupem každé logistické regresní analýzy jsou b-koeficienty. Na obrázku níže jsou uvedeny pro naše příkladová data.

Než přejdeme k podrobnostem, tento výstup stručně ukazuje

b-koeficienty, které tvoří náš model;
standardní chyby pro tyto b-koeficienty;
Waldovu statistiku – vypočtenou jako \((\frac{B}{SE})^2\)-, která se řídí chí-kvadrát rozdělením;
stupně volnosti pro Waldovu statistiku;
hladiny významnosti pro b-koeficienty;
exponenciální b-koeficienty neboli \(e^B\) jsou poměry šancí spojené se změnami skóre prediktorů;
95% interval spolehlivosti pro exponenciální b-koeficienty.

Koeficienty b doplňují náš logistický regresní model, který je nyní

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9,079\,+\,0.124\, \cdot\, age_i)}}$$

Pro 75letého klienta je pravděpodobnost úmrtí do 5 let

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0,124\, \cdot\, 75)}}=$$

$$P(death_i) = \frac{1}{1 + e^{\,-\,0,249}}=$$

$$P(death_i) = \frac{1}{1 + 0.780}=$$

$P(death_i) \aprox 0,562$$

Takže nyní víme, jak předpovědět smrt do 5 let vzhledem k něčímu věku. Jak dobrá je však tato předpověď? Existuje několik přístupů. Začněme porovnáním modelů.

Logistická regrese – základní model

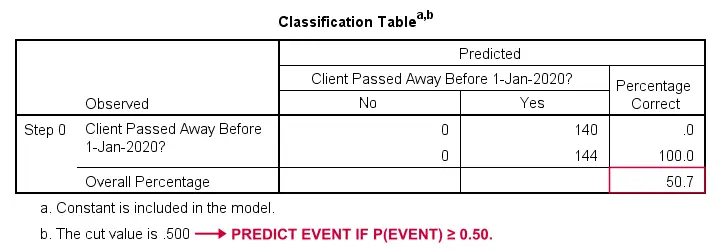
Jak bychom mohli předpovědět, kdo zemřel, kdybychom neměli žádné další informace? No, zemřelo 50,7 % našeho vzorku. Takže předpovídaná pravděpodobnost by pro všechny byla jednoduše 0,507.

Pro účely klasifikace obvykle předpovídáme, že událost nastane, pokud p(událost) ≥ 0,50. V případě, že p(událost) ≥ 0,50, předpovídáme, že událost nastane. Protože p(zemřel) = 0,507 pro všechny, jednoduše předpovíme, že všichni zemřeli. Tato předpověď je správná pro 50,7 % našeho vzorku, který zemřel.

Logistická regrese – poměr pravděpodobnosti

Nyní můžeme z těchto předpovězených pravděpodobností a pozorovaných výsledků vypočítat naši míru špatné shody: -2LL = 393,65. Náš skutečný model -předpovídající úmrtí z důvodu věku- vychází -2LL = 354,20. Rozdíl mezi těmito čísly se nazývá poměr pravděpodobnosti \(LR\):

$$LR = (-2LL_{základní hodnota}) – (-2LL_{model})$$

Důležité je, že \(LR\) má chí-kvadrát rozdělení s \(df\) stupni volnosti, vypočtené jako

$$df = k_{model} – k_{základna}$

kde \(k\) označuje počty parametrů odhadnutých modely. Jak je uvedeno v tomto Googlesheetu, výsledkem \(LR\) a \(df\) je hladina významnosti pro celý model.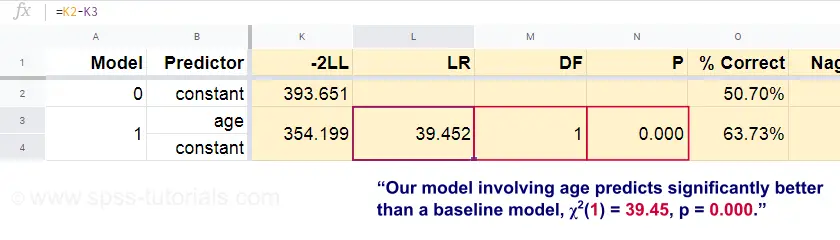

Nulová hypotéza zde zní, že některý model předpovídá stejně špatně jako základní model v určité populaci. Protože p = 0,000, zamítáme ji: náš model (předpovídající úmrtí z věku) funguje významně lépe než základní model bez jakýchkoli prediktorů.
Ale o kolik přesně lépe? Na to odpovídá jeho velikost účinku.

Logistická regrese – velikost účinku modelu

Dobrý způsob, jak posoudit, jak dobře náš model funguje, je z míry velikosti účinku. Jednou z možností je Coxovo & Snellovo R2 neboli \(R^2_{CS}\) vypočtené jako

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-\,(-2LL_{základní hodnota})}{n}}$

Naneštěstí \(R^2_{CS}\) nikdy nedosáhne svého teoretického maxima 1. Proto se často dává přednost upravené verzi známé jako Nagelkerkeho R2 nebo \(R^2_{N}\):

$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}}$$

Pro náš příklad dat je \(R^2_{CS}\) = 0,130, což znamená střední velikost účinku. \(R^2_{N}\) = 0,173, což je o něco větší než střední.

Naposledy, \(R^2_{CS}\) a \(R^2_{N}\) jsou technicky zcela odlišné od r-kvadrátu vypočteného v lineární regresi. Snaží se však plnit stejnou úlohu. Obě míry se proto označují jako pseudomíry r-kvadrátu.

Logistická regrese – velikost účinku prediktoru

Je pravda, že jen velmi málo učebnic uvádí nějakou velikost účinku pro jednotlivé prediktory. Možná je to proto, že tyto v programu SPSS zcela chybí. Důvod, proč je potřebujeme, je ten, že b-koeficienty závisí na (libovolných) stupnicích našich prediktorů:kdybychom zadali věk ve dnech místo v letech, jeho b-koeficient by se nesmírně zmenšil. To samozřejmě činí b-koeficienty nevhodnými pro porovnávání prediktorů v rámci různých modelů nebo mezi nimi.
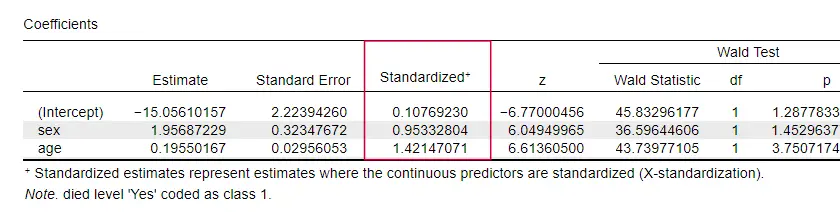
JASP obsahuje částečně standardizované b-koeficienty: kvantitativní prediktory – ale ne výslednou proměnnou – se zadávají jako z-skóre, jak je uvedeno níže.

Předpoklady logistické regrese

Logistická regresní analýza vyžaduje následující předpoklady:

1. nezávislá pozorování;
2. správná specifikace modelu;
3. bezchybné měření výsledné proměnné a všech prediktorů;
4. linearita: každý prediktor je lineárně vztažen k \(e^B\) (poměr šancí).

Předpoklad 4 je poněkud sporný a v mnoha učebnicích1,6 se vynechává. Lze jej vyhodnotit pomocí Boxova-Tidwellova testu, jak o něm pojednává Field4. V podstatě jde o testování, zda existuje nějaký interakční efekt mezi každým prediktorem a jeho přirozeným logaritmem nebo \(LN\).

Vícenásobná logistická regrese

Dosud jsme se omezili na jednoduchou logistickou regresi, která používá pouze jeden prediktor. Model lze snadno rozšířit o další prediktory, čímž vznikne vícenásobná logistická regrese:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,….+\,b_kX_{ki})}}$$

kde

• \(P(Y_i)\) je předpokládaná pravděpodobnost, že \(Y\) je pravdivé pro případ \(i\);
• \(e\) je matematická konstanta přibližně 2.72;
• \(b_0\) je konstanta odhadnutá z dat;
• \(b_1\), \(b_2\), … , \(b_k\) jsou koeficienty b pro prediktory 1, 2, … ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) jsou pozorované výsledky prediktorů \(X_1\), \(X_2\), … ,\(X_k\) pro případ \(i\).

Vícená logistická regrese často zahrnuje výběr modelu a kontrolu multikolinearity. Jinak se jedná o poměrně jednoduché rozšíření jednoduché logistické regrese.

Tento základní úvod se omezil na základní informace o logistické regresi. Pokud se chcete dozvědět více, můžete si přečíst některá témata, která jsme vynechali:

1. poměry šancí – v logistické regresi vypočtené jako \(e^B\) – vyjadřují, jak se mění pravděpodobnosti v závislosti na skóre prediktorů ;
2. Boxův-Tidwellův test zkoumá, zda jsou vztahy mezi výše zmíněnými poměry šancí a skóre prediktorů lineární;
3. Hosmerův a Lemeshowův test je alternativní test dobré shody celého modelu logistické regrese.

Díky za přečtení!

1. Warner, R.M. (2013). Aplikovaná statistika (2. vydání). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistika. The Art & Science of Learning from Data [Umění & učit se z dat]. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics (Objevování statistiky s IBM SPSS Statistics). Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statistical Methods for Psychology (5. vydání). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6. vydání). New York:

Routledge.