• Logistisk regression – ligning
• Logistisk regression – eksempelkurver
• Logistisk regression – B-koefficienter
• Logistisk regression – Effektstørrelse
• Logistisk regression Antagelser

Logistisk regression er en teknik til forudsigelse af en
dichotom udfaldsvariabel ud fra 1+ prædiktorer.Eksempel: Hvor stor er sandsynligheden for, at folk dør inden 2020, når man tager udgangspunkt i deres alder i 2015? Bemærk, at “dø” er en dikotom variabel, fordi den kun har 2 mulige udfald (ja eller nej).
Denne analyse er også kendt som binær logistisk regression eller blot “logistisk regression”. En beslægtet teknik er multinomial logistisk regression, som forudsiger udfaldsvariabler med 3+ kategorier.

Logistisk regression – simpelt eksempel

Et plejehjem har data om N = 284 klienters køn, alder pr. 1. januar 2015 og om klienten er afgået ved døden inden den 1. januar 2020. De rå data er i dette Googlesheet, delvist vist nedenfor.

Lad os først bare fokusere på alder: Kan vi forudsige død før 2020 ud fra alder i 2015?Og -hvis ja- præcist hvordan? Og i hvilket omfang? Et godt første skridt er at inspicere et spredningsdiagram som det nedenfor viste.

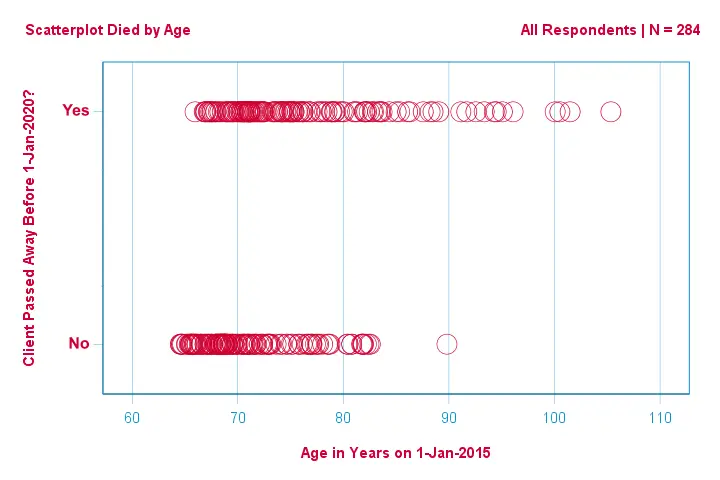Et par ting, vi ser i dette spredningsdiagram, er, at

• alle på nær én klient over 83 år døde inden for de næste 5 år;
• standardafvigelsen for alder er meget større for klienter, der døde, end for klienter, der overlevede;
• alderen har en betydelig positiv skævhed, især for de klienter, der døde.

Men hvordan kan vi forudsige, om en klient er død, i betragtning af hans alder? Det vil vi gøre ved at tilpasse en logistisk kurve.

En simpel logistisk regressionsligning

En simpel logistisk regression beregner sandsynligheden for et bestemt udfald givet en enkelt prædiktorvariabel som

$$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}}$$$

hvor

• \(P(Y_i)\) er den forudsagte sandsynlighed for, at \(Y\) er sandt for tilfældet \(i\);
• \(e\) er en matematisk konstant på ca. 2.72;
• \(b_0\) er en konstant, der er estimeret ud fra data;
• \(b_1\) er en b-koefficient, der er estimeret ud fra data;
• \(X_i\) er den observerede score på variabel \(X\) for tilfælde \(i\).

Selve essensen af logistisk regression er at estimere \(b_0\) og \(b_1\). Disse 2 tal giver os mulighed for at beregne sandsynligheden for, at en klient dør givet en hvilken som helst observeret alder. Vi vil illustrere dette med nogle eksempelkurver, som vi har tilføjet til det foregående spredningsdiagram.

Logistisk regression Eksempelkurver

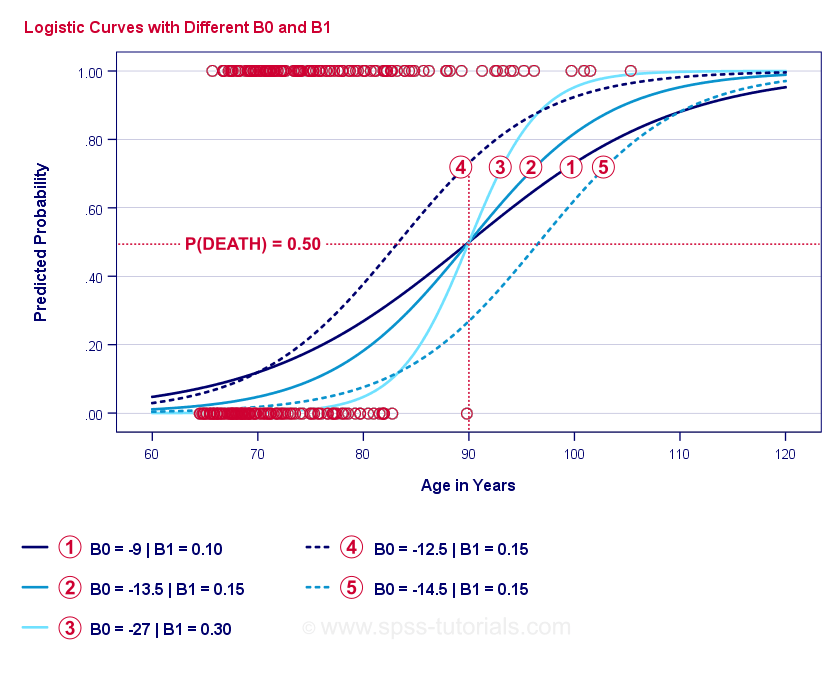
Hvis du tager dig et øjeblik til at sammenligne disse kurver, kan du se følgende:

• \(b_0\) bestemmer kurvernes horisontale position: Når \(b_0\) stiger, forskydes kurverne mod venstre, men deres stejlhed er upåvirket. Dette ses for kurverne , og . Bemærk, at \(b_0\) er forskellig, men \(b_1\) er lig med \(b_1\) for disse kurver.
• Da \(b_0\) stiger, stiger de forudsagte sandsynligheder også: givet en alder = 90 år forudsiger kurve en sandsynlighed for at dø på ca. 0,75. Kurverne og forudsiger ca. 0,50 og 0,25 sandsynlighed for at dø for en 90-årig klient.
• \(b_1\) bestemmer stejlheden af kurverne: hvis \(b_1\) > 0, stiger sandsynligheden for at dø med stigende alder. Denne sammenhæng bliver stærkere, når \(b_1\) bliver større. Kurverne , og illustrerer dette punkt: når \(b_1\) bliver større, bliver kurverne stejlere, så sandsynligheden for at dø stiger hurtigere med stigende alder.

For nu har vi ét spørgsmål tilbage: Hvordan finder vi de “bedste” \(b_0\) og \(b_1\)?

Logistisk regression – log sandsynlighed

For hver respondent estimerer en logistisk regressionsmodel sandsynligheden for, at en eller anden begivenhed \(Y_i\) er indtruffet. Disse sandsynligheder skal naturligvis være høje, hvis hændelsen faktisk er indtruffet, og omvendt. En måde at sammenfatte, hvor godt en eller anden model klarer sig for alle respondenter, er log-likelihood \(LL\):

$$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$$ hvor

• \(Y_i\) er 1, hvis begivenheden har fundet sted, og 0, hvis den ikke har fundet sted;
• \(ln\) betegner den naturlige logaritme: til hvilken potens skal man hæve \(e\) for at opnå et givet tal?

\(LL\) er et mål for god tilpasning: alt andet lige passer en logistisk regressionsmodel bedre til dataene i det omfang, \(LL\) er større. Noget forvirrende er det, at \(LL\) altid er negativ. Så vi ønsker at finde de \(b_0\) og \(b_1\), for hvilke
\(LL\) er så tæt på nul som muligt.

Maximum Likelihood Estimation

I modsætning til lineær regression kan logistisk regression ikke uden videre beregne de optimale værdier for \(b_0\) og \(b_1\). I stedet er vi nødt til at prøve forskellige tal, indtil \(LL\) ikke stiger yderligere. Hvert sådant forsøg er kendt som en iteration. Processen med at finde optimale værdier gennem sådanne iterationer er kendt som maximum likelihood estimation.

Så det er i princippet sådan, at statistisk software – såsom SPSS, Stata eller SAS – får logistiske regressionsresultater. Heldigvis er de utrolig gode til det. Men i stedet for at rapportere \(LL\) rapporterer disse pakker \(-2LL\). \(-2LL\) er et “badness-of-fit”-mål, som følger en
chi-square-fordeling. \(-2LL\) er derfor nyttigt til at sammenligne forskellige modeller, som vi vil se om lidt. \(-2LL\) betegnes som -2 Log likelihood i det nedenfor viste output.

Fodnoten her fortæller os, at maximum likelihood-estimationen kun krævede 5 iterationer for at finde de optimale b-koefficienter \(b_0\) og \(b_1\). Så lad os se på dem nu.

Logistisk regression – B-koefficienter

Det vigtigste output for enhver logistisk regressionsanalyse er b-koefficienterne. Figuren nedenfor viser dem for vores eksempeldata.

Hvor vi går i detaljer, viser dette output kort

de b-koefficienter, der udgør vores model;
standardfejlene for disse b-koefficienter;
Wald-statistikken – beregnet som \((\frac{B}{SE})^2\)- som følger en chi-square-fordeling;
frihedsgrader for Wald-statistikken;
signifikansniveauer for b-koefficienterne;
eksponerede b-koefficienter eller \(e^B\) er de odds ratio’er, der er forbundet med ændringer i prædiktor-scoren;
95 % konfidensinterval for de eksponerede b-koefficienter.

B-koefficienterne supplerer vores logistiske regressionsmodel, som nu er

$$$P(death_i) = \frac{1}{1 + e^{\,-\,-\,(-9,079\,+\,0.124\, \cdot\, age_i)}}}$$$

For en 75-årig kunde er sandsynligheden for at dø inden for 5 år

$$$P(death_i) = \frac{1}{1 + e^{\,-\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}}=$$$

$$$P(death_i) = \frac{1}{1 + e^{\,-\,-\,0.249}}=$$$

$$$P(death_i) = \frac{1}{1 + 0.780}=$$$

$$$P(death_i) \approx 0.562$$$

Så nu ved vi, hvordan vi kan forudsige døden inden for 5 år givet en persons alder. Men hvor god er denne forudsigelse? Der er flere tilgange. Lad os starte med at sammenligne modeller.

Logistisk regression – basismodel

Hvordan kunne vi forudsige, hvem der døde, hvis vi ikke havde andre oplysninger? Jo, 50,7 % af vores stikprøve gik bort. Så den forudsagte sandsynlighed ville simpelthen være 0,507 for alle.

Til klassifikationsformål forudsiger vi normalt, at en begivenhed indtræffer, hvis p(begivenhed) ≥ 0,50. Da p(døde) = 0,507 for alle, forudsiger vi simpelthen, at alle er døde. Denne forudsigelse er korrekt for de 50,7 % af vores stikprøve, der døde.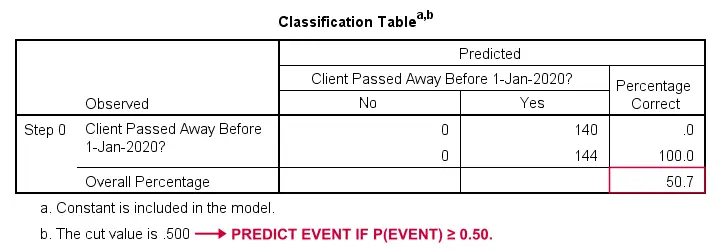

Logistisk regression – Likelihood Ratio

Nu kan vi ud fra disse forudsagte sandsynligheder og de observerede udfald beregne vores mål for dårlighed af tilpasning: -2LL = 393,65. Vores faktiske model – som forudsiger død på grund af alder – giver -2LL = 354,20. Forskellen mellem disse tal er kendt som sandsynlighedskvotienten \(LR\):

$$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Væsentligt er, at \(LR\) følger en chi-square-fordeling med \(df\) frihedsgrader, beregnet som

$$$df = k_{model} – k_{baseline}}$$$

hvor \(k\) angiver antallet af parametre, der er estimeret af modellerne. Som det fremgår af dette Googlesheet, resulterer \(LR\) og \(df\) i et signifikansniveau for hele modellen.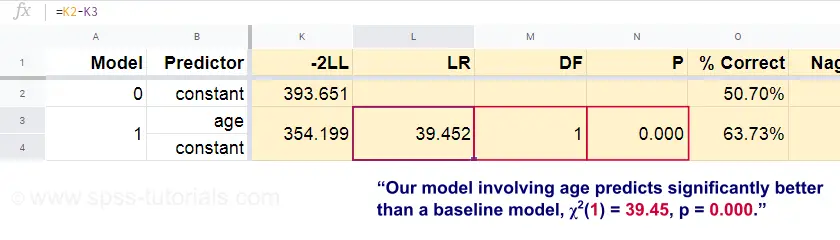

Nulhypotesen er her, at en eller anden model forudsiger lige så dårligt som basismodellen i en eller anden population. Da p = 0,000, forkaster vi dette: Vores model (der forudsiger død på grund af alder) klarer sig signifikant bedre end en basismodel uden nogen prædiktorer.
Men hvor meget bedre præcist? Dette besvares ved hjælp af dens effektstørrelse.

Logistisk regression – modellens effektstørrelse

En god måde at vurdere, hvor godt vores model klarer sig på, er ud fra et mål for effektstørrelse. En mulighed er Cox & Snell R2 eller \(R^2_{CS}\) beregnet som

$$$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-\,(-2LL_{baseline})}{n}}$$$

Sværre når \(R^2_{CS}\) aldrig op på sit teoretiske maksimum på 1. Derfor foretrækkes ofte en justeret version kendt som Nagelkerke R2 eller \(R^2_{N}\):

$$$$R^2_{N} = \frac{R^2_{CS}}}{1 – e^{-\frac{-2LL_{baseline}}}{n}}}$$$

For vores eksempeldata er \(R^2_{CS}\) = 0,130, hvilket angiver en middelstor effektstørrelse. \(R^2_{N}\) = 0,173, hvilket er lidt større end medium.

Sidst er \(R^2_{CS}\) og \(R^2_{N}\) teknisk set helt forskellige fra r-square som beregnet i lineær regression. De forsøger dog at udfylde den samme rolle. Begge mål er derfor kendt som pseudo r-square-mål.

Logistisk regression – prædiktorens effektstørrelse

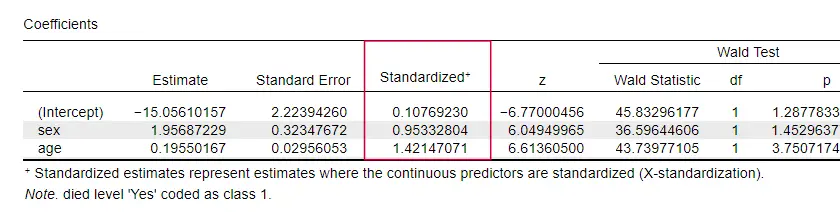
Der er mærkeligt nok meget få lærebøger, der nævner nogen effektstørrelse for individuelle prædiktorer. Måske er det fordi disse er helt fraværende i SPSS. Grunden til, at vi har brug for dem, er, at b-koefficienterne afhænger af vores prædiktorers (vilkårlige) skalaer: Hvis vi havde indtastet alder i dage i stedet for år, ville dens b-koefficient skrumpe enormt. Dette gør naturligvis b-koefficienter uegnede til at sammenligne prædiktorer inden for eller på tværs af forskellige modeller.
JASP indeholder delvist standardiserede b-koefficienter: kvantitative prædiktorer -men ikke udfaldsvariablen- indtastes som z-scores, som vist nedenfor.

Logistiske regressionsforudsætninger

Logistisk regressionsanalyse kræver følgende forudsætninger:

1. uafhængige observationer;
2. korrekt modelspecifikation;
3. fejlfri måling af udfaldsvariablen og alle prædiktorer;
4. linearitet: hver prædiktor er lineært relateret til \(e^B\) (odds ratio).

Hypotese 4 er noget omstridt og udelades af mange lærebøger1,6. Den kan evalueres med Box-Tidwell-testen som diskuteret af Field4. Dette går grundlæggende ud på at teste, om der er nogen interaktionseffekter mellem hver prædiktor og dens naturlige logaritme eller \(LN\).

Multipel logistisk regression

Den hidtidige diskussion var begrænset til simpel logistisk regression, som kun anvender én prædiktor. Modellen kan let udvides med yderligere prædiktorer, hvilket resulterer i multipel logistisk regression:

$$$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,…+\,b_kX_{ki})}}}$$$ hvor

• \(P(Y_i)\) er den forudsagte sandsynlighed for, at \(Y\) er sandt for tilfældet \(i\);
• (e\) er en matematisk konstant på ca. 2.72;
• \(b_0\) er en konstant, der er estimeret ud fra dataene;
• \(b_1\), \(b_2\), … ,\(b_k\) er b-koefficienten for prædiktorerne 1, 2, … ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) er observerede scorer på prædiktorerne \(X_1\), \(X_2\), …. ,\(X_k\) for case \(i\).

Multipel logistisk regression indebærer ofte modelvalg og kontrol af multikollinearitet. Ellers er det en ret ukompliceret udvidelse af simpel logistisk regression.

Denne grundlæggende introduktion var begrænset til det væsentlige i logistisk regression. Hvis du gerne vil lære mere, kan du læse op på nogle af de emner, vi udelod:

1. odds ratioer – beregnet som \(e^B\) i logistisk regression – udtrykker, hvordan sandsynlighederne ændrer sig afhængigt af prædiktor-scores ;
2. Box-Tidwell-testen undersøger, om relationerne mellem de førnævnte odds ratioer og prædiktor-scores er lineære;
3. Hosmer og Lemeshow-testen er en alternativ goodness-of-fit-test for en hel logistisk regressionsmodel.

Tak for læsning!

1. Warner, R.M. (2013). Anvendt statistik (2. udgave). Thousand Oaks, CA: SAGE.
3. Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
4. Hair, J.F., Black, W.C., Black, W.C., Babin, B.J. et al (2006). Multivariat dataanalyse. New Jersey: Pearson Prentice Hall.
5. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics (Opdag statistik med IBM SPSS Statistics). Newbury Park, CA: Sage.
6. Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
8. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.