Logistinen regressio - Aloittelijan opas

Logistisen regression yhtälö
Logistisen regression esimerkkikäyrät
Logistisen regression – B-kertoimet
Logistinen regressio – Efektikoko
Logistisen regression oletukset

Logistinen regressio on tekniikka, jolla ennustetaan
dikotomista tulosmuuttujaa 1+ ennustajista.Esimerkki: Kuinka todennäköisesti ihmiset kuolevat ennen vuotta 2020, kun otetaan huomioon heidän ikänsä vuonna 2015? Huomaa, että ”kuolee” on dikotominen muuttuja, koska sillä on vain kaksi mahdollista lopputulosta (kyllä tai ei).
Tämä analyysi tunnetaan myös nimellä binäärinen logistinen regressio tai yksinkertaisesti ”logistinen regressio”. Tähän liittyvä tekniikka on multinomiaalinen logistinen regressio, joka ennustaa lopputulosmuuttujia, joissa on 3+ luokkaa.

Logistinen regressio – yksinkertainen esimerkki

Hoitokodilla on tiedot N = 284 asiakkaan sukupuolesta, iästä 1.1.2015 ja siitä, onko asiakas kuollut ennen 1.1.2020. Raakadata on tässä Googlesheetissä, osittain esitetty alla.

Keskitytään ensin vain ikään:voiko vuoden 2015 iästä ennustaa kuoleman ennen vuotta 2020?Ja -jos voi- tarkalleen miten? Ja missä määrin? Hyvä ensimmäinen askel on tarkastella alla olevan kaltaista hajontakuviota.

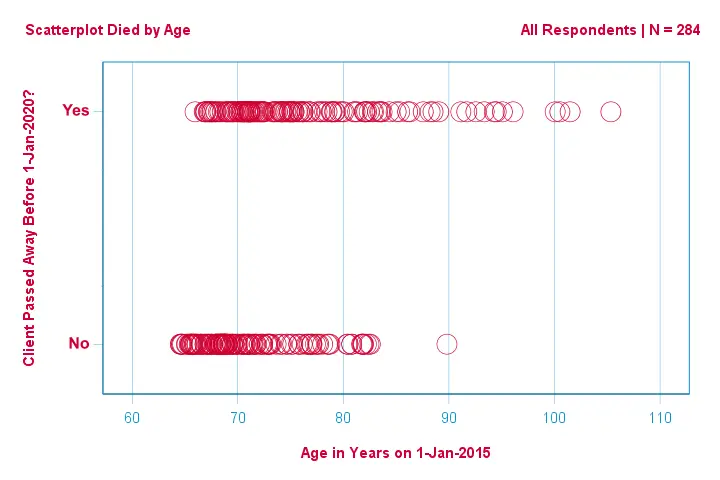
Muutamia asioita, jotka näemme tässä hajontakuviossa, ovat seuraavat:

yhtä lukuun ottamatta kaikki yli 83-vuotiaat asiakkaat kuolivat seuraavien viiden vuoden aikana;
iän keskihajonta on paljon suurempi kuolleiden kuin eloonjääneiden asiakkaiden kohdalla; iällä on huomattavan paljon positiivista vinoutumaa, erityisesti kuolleiden asiakkaiden kohdalla.

Mutta miten voimme ennustaa, onko asiakas kuollut, ottaen huomioon hänen ikänsä? Teemme juuri sen sovittamalla logistisen käyrän.

Simppeli logistisen regression yhtälö

Simppeli logistinen regressio laskee jonkin lopputuloksen todennäköisyyden yhden ennustemuuttujan perusteella seuraavasti

$$P(Y_i) = \frac{1}{1 + e^{\\,-\\,(b_0\,+\,b_1X_{1i})}}}$$

jossa

$P(Y_i)$ on ennustettu todennäköisyys sille, että $Y$ on tosi tapauksessa $i$;
$e$ on matemaattinen vakio, joka on noin 2.72;
$b_0$ on aineistosta estimoitu vakio;
$b_1$ on aineistosta estimoitu b-kerroin;
$X_i$ on muuttujan $X$ havaittu pistemäärä tapauksen $i$ osalta.

Logistisen regression ydin on $b_0$ ja $b_1$ estimointi. Näiden kahden luvun avulla voimme laskea todennäköisyyden, jolla asiakas kuolee minkä tahansa havaitun iän perusteella. Havainnollistamme tätä muutamalla esimerkkikäyrällä, jotka lisäsimme edelliseen hajontakuvioon.

Logistisen regression esimerkkikäyrät

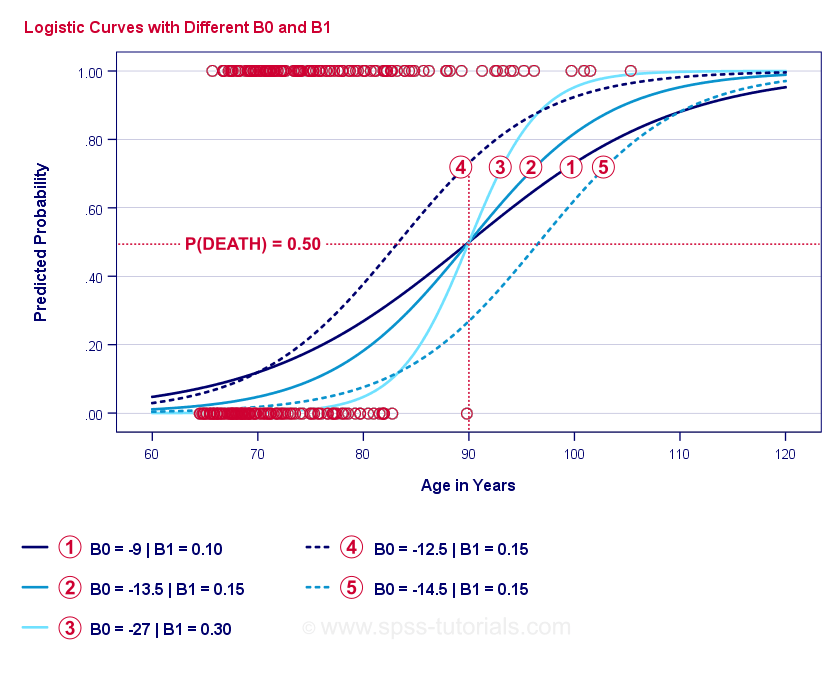
Jos käytät hetken aikaa vertaillaksesi näitä käppyröitä, voit havaita seuraavaa:

$b_0$ määrää käyrien vaakasuoran sijainnin: kun $b_0$ kasvaa, käyrät siirtyvät vasemmalle, mutta niiden jyrkkyys ei vaikuta. Tämä nähdään käyrien , ja osalta. Huomaa, että $b_0$ on erilainen mutta $b_1$ on sama näille käyrille.
Kun $b_0$ kasvaa, myös ennustetut todennäköisyydet kasvavat: kun ikä = 90 vuotta, käyrä ennustaa noin 0,75 todennäköisyyttä kuolla. Käyrät ja ennustavat noin 0,50 ja 0,25 todennäköisyyttä kuolla 90-vuotiaalle asiakkaalle.
$b_1$ määrää käyrien jyrkkyyden: jos $b_1$ > 0, kuoleman todennäköisyys kasvaa iän kasvaessa. Tämä suhde vahvistuu, kun $b_1$ kasvaa. Käyrät , ja havainnollistavat tätä seikkaa: kun $b_1$ kasvaa, käyrät jyrkkenevät, joten kuoleman todennäköisyys kasvaa nopeammin iän kasvaessa.

Nyt on vielä yksi kysymys jäljellä: miten löydämme ”parhaat” $b_0$ ja $b_1$?

Logistinen regressio – logistinen todennäköisyys

Kullekin vastaajalle logistinen regressiomalli arvioi todennäköisyyden, että jokin tapahtuma $Y_i$ on tapahtunut. Ilmeisesti näiden todennäköisyyksien pitäisi olla suuria, jos tapahtuma todella tapahtui, ja päinvastoin. Yksi tapa tiivistää, kuinka hyvin jokin malli toimii kaikkien vastaajien osalta, on log-likelihood $LL$:

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$$

missä

$Y_i$ on 1, jos tapahtuma tapahtui, ja 0, jos ei tapahtunut;
$ln$ tarkoittaa luonnollista logaritmia: mihin potenssiin on korotettava $\(e$, jotta saadaan tietty luku?

$LL$ on sopivuuden hyvyyden mittari: jos kaikki muut tekijät pysyvät ennallaan, logistinen regressiomalli sopii aineistoon paremmin sikäli kuin $LL$ on suurempi. Hieman hämmentävää kyllä, $LL$ on aina negatiivinen. Haluamme siis löytää $b_0$ ja $b_1$, joille
$LL$ on mahdollisimman lähellä nollaa.

Maximum Likelihood Estimation

Toisin kuin lineaarisessa regressiossa, logistisessa regressiossa ei voida helposti laskea optimaalisia arvoja $b_0$ ja $b_1$. Sen sijaan meidän on kokeiltava eri lukuja, kunnes $LL$ ei enää kasva. Jokaista tällaista yritystä kutsutaan iteraatioksi. Optimaalisten arvojen löytämistä tällaisten iteraatioiden avulla kutsutaan suurimman todennäköisyyden estimoinniksi (maximum likelihood estimation).

Näin siis periaatteessa tilasto-ohjelmat – kuten SPSS, Stata tai SAS – saavat logistisen regression tulokset. Onneksi ne ovat siinä hämmästyttävän hyviä. Mutta sen sijaan, että nämä paketit ilmoittaisivat $LL$, ne ilmoittavat $-2LL$.$-2LL$ on ”badness-of-fit”-mitta, joka noudattaa
chi-neliö-jakaumaa.Tämä tekee $-2LL$:sta hyödyllisen eri mallien vertailussa, kuten näemme pian. Alla olevassa tulosteessa $-2LL$ on merkitty -2 Log likelihoodiksi.

Alaviite kertoo, että maksimilikelihood-estimointi tarvitsi vain 5 iteraatiota optimaalisten b-kertoimien $b_0$ ja $b_1$ löytämiseksi. Tutkitaan siis nyt niitä.

Logistinen regressio – B-kertoimet

Minkä tahansa logistisen regressioanalyysin tärkein tuotos ovat b-kertoimet. Alla olevassa kuvassa esitetään ne esimerkkiaineistomme osalta.

Ennen kuin menemme yksityiskohtiin, tämä tuloste näyttää lyhyesti

b-kertoimet, jotka muodostavat mallimme;
näiden b-kertoimien keskivirheet;
Wald-statistiikan, joka lasketaan muodossa $(\frac{B}{SE})^2$- ja joka noudattaa chi-neliöjakaumaa;
Wald-statistiikan vapausasteet;
b-kertoimien merkitsevyystasot;
eksponentoidut b-kertoimet eli $e^B$ ovat ennustepistemäärien muutoksiin liittyviä kertoimien suhdelukuja;
95 %:n luottamusväli eksponentoituja b-kertoimia varten.

B-kertoimet täydentävät logistisen regressiomallimme, joka on nyt

$$P(kuolema_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, ikä_i)}}}$$

75-vuotiaalle asiakkaalle todennäköisyys kuolla 5 vuoden kuluessa on

$$P(kuolema_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}}=$$

$$P(kuolema_i) = \frac{1}{1 + e^{\,-\,0.249}}}=$$

$$P(kuolema_i) = \frac{1}{1 + 0.780}=$$

$$$P(kuolema_i) \approx 0.562$$

Tiedämme siis nyt, miten voimme ennustaa kuoleman 5 vuoden sisällä jonkun henkilön iän perusteella. Mutta kuinka hyvä tämä ennuste on? On olemassa useita lähestymistapoja. Aloitetaan mallien vertailulla.

Logistinen regressio – perusmalli

Miten voisimme ennustaa, kuka on kuollut, jos meillä ei ole mitään muuta tietoa? No, 50,7 % otoksestamme menehtyi. Joten ennustettu todennäköisyys olisi yksinkertaisesti 0,507 kaikille.

Luokittelua varten ennustamme yleensä, että tapahtuma tapahtuu, jos p(tapahtuma) ≥ 0,50. Koska p(kuoli) = 0,507 kaikille, ennustamme yksinkertaisesti, että kaikki kuolivat. Tämä ennuste pitää paikkansa niiden 50,7 %:n osalta otoksestamme, jotka kuolivat.

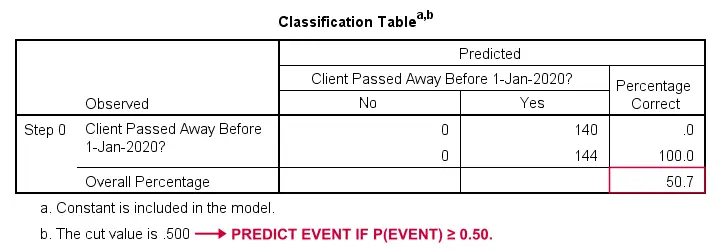
Logistinen regressio – Todennäköisyyssuhde

Nyt näistä ennustetuista todennäköisyyksistä ja havaituista lopputuloksista voimme laskea huono-osaisuusmittarimme: -2LL = 393.65. Varsinainen mallimme – joka ennustaa kuoleman iän perusteella – antaa tulokseksi -2LL = 354.20. Näiden lukujen välinen ero tunnetaan todennäköisyyssuhteena $LR$:

$$LR = (-2LL_{perustaso}) – (-2LL_{malli})$$

Tärkeää on, että $LR$ noudattaa khiin neliöjakaumaa, jonka vapausasteet ovat $df$, joka lasketaan muodossa

$$df = k_{malli} – k_{perusviiva}$$

jossa $k$ tarkoittaa mallien estimoimien parametrien lukumäärää. Kuten tässä Googlesheetissä näkyy, $LR$ ja $df$ johtavat koko mallin merkitsevyystasoon.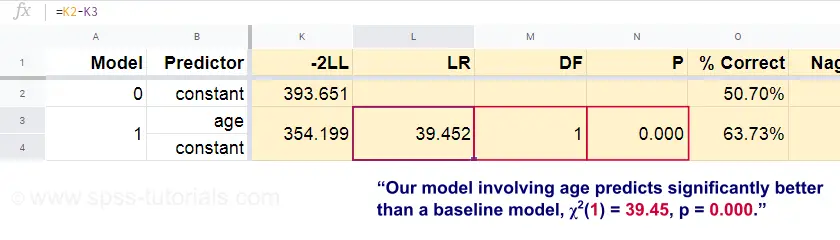

Nollahypoteesi tässä on, että jokin malli ennustaa yhtä huonosti kuin perusmalli jossain populaatiossa. Koska p = 0.000, hylkäämme tämän: mallimme (joka ennustaa kuoleman iän perusteella) toimii merkitsevästi paremmin kuin perusmalli, jossa ei ole mitään ennusteita.
Mutta kuinka paljon paremmin tarkalleen ottaen? Tähän vastaa sen efektikoko.

Logistinen regressio – mallin efektikoko

Hyvä tapa arvioida, kuinka hyvin mallimme toimii, on efektikokomittarin avulla. Yksi vaihtoehto on Coxin & Snellin R2 eli $R^2_{CS}$, joka lasketaan seuraavasti

$$$R^2_{CS} = 1 – e^{\frac{(-2LL_{malli})\,-\,(-2LL_{lähtötilanne})}{n}}$$$

Pahanlaatuisesti $R^2_{CS}$ ei koskaan saavuta teoreettista maksimiaan 1. Siksi usein suositaan korjattua versiota, joka tunnetaan nimellä Nagelkerke R2 tai $R^2_{N}$:

$$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{perusviiva}}}{n}}}$$

Esimerkkiaineistollamme $R^2_{CS}$ = 0.130, mikä viittaa keskinkertaiseen vaikutuksen kokoon. $R^2_{N}$ = 0.173, mikä on hieman suurempi kuin keskisuuri.

Viimeiseksi, $R^2_{CS}$ ja $R^2_{N}$ ovat teknisesti täysin erilaisia kuin lineaarisessa regressiossa laskettu r-neliö. Ne pyrkivät kuitenkin täyttämään saman tehtävän. Molempia mittareita kutsutaankin pseudo-r-neliömittareiksi.

Logistinen regressio – Ennustajan efektikoko

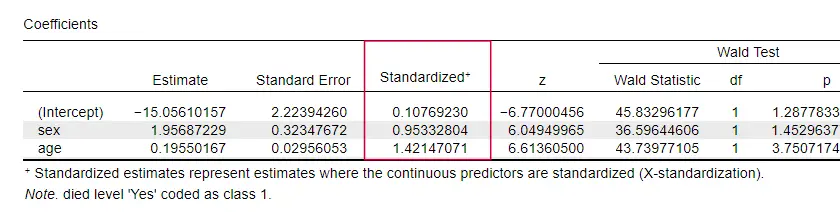
Hyvin harvoissa oppikirjoissa mainitaan mitään efektikokoa yksittäisille ennustajille. Ehkä se johtuu siitä, että nämä puuttuvat kokonaan SPSS:stä. Syy, miksi tarvitsemme niitä, on se, että b-kertoimet riippuvat ennustajiemme (mielivaltaisista) asteikoista: jos antaisimme iän päivinä vuosien sijasta, sen b-kerroin kutistuisi valtavasti. Tämä luonnollisesti tekee b-kertoimista sopimattomia vertailtaessa ennustajia eri mallien sisällä tai eri mallien välillä.
JASP sisältää osittain standardoidut b-kertoimet: kvantitatiiviset ennustajat – mutta ei lopputulosmuuttujaa – syötetään z-pisteinä, kuten alla on esitetty.

Logistisen regression oletukset

Logistinen regressioanalyysi edellyttää seuraavia oletuksia:

riippumattomat havainnot;
korrekti mallin spesifikaatio;
loppumuuttujan ja kaikkien ennustemuuttujien virheettömät mittaustulokset;
lineaarisuus: kukin ennustemuuttuja korreloituu suoraviivaisesti $e^B $:n (todennäköisyyssuhde) kanssa.

Oletus 4 on jossain määrin kiistanalainen ja jätetään pois monista oppikirjoista1,6. Sitä voidaan arvioida Fieldin4 käsittelemällä Box-Tidwellin testillä. Kyse on pohjimmiltaan siitä, että testataan, onko kunkin ennustajan ja sen luonnollisen logaritmin tai $LN$ välillä vuorovaikutusvaikutuksia.

Moninkertainen logistinen regressio

Keskustelumme on toistaiseksi rajoittunut yksinkertaiseen logistiseen regressioon, jossa käytetään vain yhtä ennustetta. Mallia on helppo laajentaa ylimääräisillä ennustajilla, jolloin saadaan moninkertainen logistinen regressio:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,….+\,b_kX_{ki})}}$$