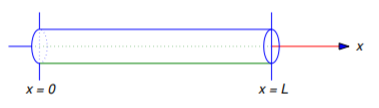
Zaczynamy badanie równań różniczkowych cząstkowych od problemu przepływu ciepła w jednorodnym pręcie o długości ⅓, umieszczonym na osi ⅓ z jednym końcem w punkcie początkowym, a drugim w punkcie ⅓ (rysunek ⅓).
Zakładamy, że pręt jest doskonale izolowany, z wyjątkiem ewentualnie jego końców, oraz że temperatura jest stała na każdym przekroju poprzecznym i dlatego zależy tylko od \(x\) i \(t\). Zakładamy również, że właściwości termiczne pręta są niezależne od \(x\) i \(t\). W takim przypadku można pokazać, że temperatura \(u = u(x, t)\) w czasie \(t) w punkcie \(x) jednostek od początku spełnia równanie różniczkowe cząstkowe
, gdzie \(a) jest dodatnią stałą określoną przez własności termiczne. Jest to równanie cieplne.
Aby wyznaczyć temperaturę w każdym punkcie pręta, gdy t=0, powiedzmy
Nazywamy to warunkiem początkowym. Musimy również określić warunki brzegowe, które muszą być spełnione na końcach pręta dla wszystkich \(t>0\). Problem ten nazwiemy problemem wartości początkowej i granicznej.
Zaczynamy od warunków brzegowych \(u(0,t)=u(L,t)=0\), a problem wartości początkowej i granicznej zapisujemy jako
Nasza metoda rozwiązania tego problemu nazywa się separacją zmiennych (nie mylić z metodą separacji zmiennych używaną w rozdziale 2.2 do rozwiązywania równań różniczkowych zwyczajnych). Zaczynamy od poszukiwania funkcji postaci
, które nie są identycznie zerowe i spełniają
dla wszystkich funkcji ((x,t)\). Ponieważ
(v_t=a^2v_{xx}}) wtedy i tylko wtedy, gdy
, co przepisujemy jako
Ponieważ wyrażenie po lewej jest niezależne od ^x, zaś wyrażenie po prawej jest niezależne od ^t, to równanie może zachodzić dla wszystkich \((x,t)\) tylko wtedy, gdy obie strony są równe tej samej stałej, którą nazywamy stałą rozdzielenia i zapisujemy jako \(-lambda\); zatem,
jest to równoważne
i
Ponieważ \(v(0, Zatem \(\) musi być wartością własną problemu wartości brzegowej
i \(X) musi być funkcją własną \(\). Z Twierdzenia 11.1.2 wynika, że wartościami własnymi równania \ref{eq:12.1.3} są \(\lambda_n=n^2\pi^2/L^2\), z powiązanymi funkcjami własnymi
Podstawiając \(\lambda=n^2\pi^2/L^2\) do równania \ref{eq:12.1.2} daje wynik
, który ma rozwiązanie
Teraz niech
Ponieważ
(v_n) spełnia równanie \ref{eq:12.1.1} z \(f(x)= \sin n\pi x/L\).
Twierdzenie
Oficjalne rozwiązanie problemu wartości początkowej i granicznej
.problemu wartości granicznej
jest
gdzie
jest szeregiem sinusoidalnym Fouriera ∗ na ∗; W tej definicji używamy terminu „rozwiązanie formalne”, ponieważ nie jest prawdą, że nieskończony szereg w równaniu \ref{eq:12.1.5} faktycznie spełnia wszystkie wymagania równania problemu początkowej wartości granicznej, gdy tak jest, mówimy, że jest to rzeczywiste rozwiązanie równania \ref{eq:12.1.4}.
Z powodu ujemnych wykładników w równaniu \ref{eq:12.1.5}, \(u\) jest zbieżne dla wszystkich \((x,t)\) z \(t>0\) (Ćwiczenie 12.1.54). Ponieważ każdy wyraz w równaniu \ref{eq:12.1.5} spełnia równanie ciepła i warunki brzegowe z równania \ref{eq:12.1.4}, \(u) ma również te własności, jeśli \(u_t) i \(u_{xx}} można uzyskać przez różniczkowanie szeregu w równaniu \ref{eq:12.1.5} warunek po warunku raz w odniesieniu do \(t) i dwa razy w odniesieniu do \(x), dla \(t>0\). Nie zawsze jednak uzasadnione jest różniczkowanie nieskończonego szeregu termin po terminie. Następne twierdzenie podaje użyteczny warunek wystarczający na zasadność różniczkowania szeregu nieskończonego termin po terminie. Pomijamy dowód.
Twierdzenie
Seria nieskończona zbieżna
może być różniczkowana warunek po warunku na zamkniętym przedziale, aby otrzymać
pochodne w punktach z=z_1} i z=z_2} są jednostronne.jednostronne, pod warunkiem, że \(w_n’\) jest ciągła na \(\) i
gdzie \(M_1,\) \(M_2,\) …, \(M_n, \) …, są stałymi takimi, że szereg \(\suma{n=1}^^wfty M_n\) jest zbieżny.
Twierdzenie \(\), zastosowane dwa razy z \(z=x\) i raz z \(z=t\), pokazuje, że \(u_{xx}\) i \(u_t\) można otrzymać przez różniczkowanie \(u\) warunek po warunku, jeśli \(t>0\) (Ćwiczenie 12.1.54). Zatem u(u)spełnia równanie ciepła i warunki brzegowe z równania \ref{eq:12.1.4} dla \(t>0\). Zatem, ponieważ \(u(x,0)=S(x)\) dla \(0\)\), \(u)\) jest rzeczywistym rozwiązaniem równania \ref{eq:12.1.4} wtedy i tylko wtedy, gdy \(S(x)=f(x)\) dla \(0\)\). Z Twierdzenia 11.3.2 wynika, że jest to prawdą, jeśli f jest ciągła i jednostronnie gładka na rzedzie, a f(0)=f(L)=0).
W tym rozdziale zdefiniujemy formalne rozwiązania kilku rodzajów problemów. Kiedy prosimy Cię o rozwiązanie takich problemów, zawsze mamy na myśli, że powinieneś znaleźć formalne rozwiązanie.
Przykład \(\PageIndex{1})
Rozwiąż równanie \ref{eq:12.1.4}z \(f(x)=x(x^2-3Lx+2L^2)\).
Rozwiązanie
Z przykładu wynika
Therefore
Jeżeli oba końce pręta są izolowane tak, że nie może przez nie przepływać ciepło, to warunki brzegowe wynoszą
Pozostawiamy Tobie (Ćwiczenie 12.1.1) wykorzystanie metody separacji zmiennych i Twierdzenia 11.1.3 do uzasadnienia następnej definicji.
Twierdzenie
Formalnym rozwiązaniem problemu wartości początkowej-granicznej
jest
gdzie
jest szereg cosinusowy Fouriera ∗ na ∗
;\), czyli,
Przykład \(\PageIndex{2})
rozwiąż równanie \{eq:12.1.6} z \(f(x)=x\).
Rozwiązanie
Z Przykładu 11.3.1 wynika, że szereg kosinusowy Fouriera \(f) na \ wynosi
Wobec tego
Pozostawiamy Tobie (Ćwiczenie 12.1.2) wykorzystanie metody separacji zmiennych i Twierdzenia 11.1.4 do uzasadnienia następnej definicji.
Twierdzenie
Formalnym rozwiązaniem problemu wartości początkowej-granicznej
jest
gdzie
jest mieszany szereg sinusoidalny Fouriera ∗ na ∗
;\), to znaczy,
Przykład \(\PageIndex{3}})
rozwiąż równanie \{eq:12.1.7} z \(f(x)=x\).
Rozwiązanie
Z przykładu 11.3.4, mieszany szereg sinusoidalny Fouriera \(f)\ na \ wynosi
Stąd
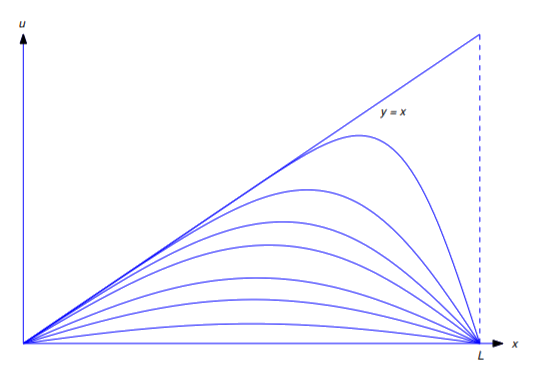
Rysunek \(\PageIndex{2}} przedstawia wykres \(u=u(x,t)\) wykreślony względem \(x)\) dla różnych wartości \(t)\). Linia \(y=x\) odpowiada \(t=0\). Pozostałe krzywe odpowiadają dodatnim wartościom \(t). Wraz ze wzrostem wartości t, wykresy zbliżają się do linii \(u=0\).
Zostawiamy Ci (Ćwiczenie 12.1.3) wykorzystanie metody separacji zmiennych i Twierdzenia 11.1.5 do uzasadnienia następnej definicji.
Twierdzenie
Formalne rozwiązanie problemu wartości początkowej i granicznej
.problemu wartości granicznej
jest
gdzie
jest mieszanym szeregiem kosinusowym Fouriera ∗ na ∗; to znaczy,
Przykład \(\PageIndex{4}})
rozwiąż równanie \ref{eq:12.1.8} z \(f(x)=x-L\).
Rozwiązanie
Z przykładu 11.3.3, mieszany szereg kosinusowy Fouriera dla f(f) na ∗ wynosi
Therefore
Usługiwanie się technologią
Doświadczenia numeryczne mogą zwiększyć zrozumienie rozwiązań problemów z początkowymi wartościami brzegowymi. Konkretnie, rozważmy formalne rozwiązanie
równania \ref{eq:12.1.4}, gdzie
jest szeregiem sinusów Fouriera \(f\) na \(\). Dla kilku ustalonych wartości t (w tym t=0) wykres zależności u_m(x,t)od t. W niektórych przypadkach użyteczne może być wykreślenie krzywych odpowiadających różnym wartościom \(t) na tych samych osiach, w innych przypadkach możesz chcieć wykreślić różne krzywe kolejno (dla rosnących wartości \(t)) i stworzyć prymitywny obraz ruchu na monitorze. Powtórz ten eksperyment dla kilku wartości ∗, aby porównać, jak wyniki zależą od ∗ dla małych i dużych wartości ∗. Należy jednak pamiętać, że znaczenia słów „mały” i „duży” zależą w tym przypadku od stałych ^2 i ^2. Dobrym sposobem na poradzenie sobie z tym problemem jest przepisanie równania {eq:12.1.12} jako
gdzie
i sporządzenie wykresu \(u_m\) względem \(x\) dla wybranych wartości \(\tau\).
Powyższe uwagi odnoszą się również do sytuacji rozważanych w Twierdzeniach \(\), z tym że równanie \(\) powinno być zastąpione równaniem \(\).1.13} powinno być zastąpione przez
w Twierdzeniach \(\PageIndex{4}} i \(\PageIndex{5}}.