Wprowadzenie

Drzewo decyzyjne jest rodzajem algorytmu uczenia nadzorowanego, który może być stosowany zarówno w problemach regresji, jak i klasyfikacji. Działa ono zarówno dla kategorycznych, jak i ciągłych zmiennych wejściowych i wyjściowych.

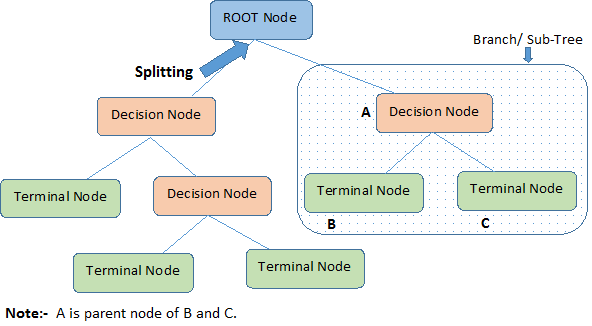
Zidentyfikujmy ważne terminologie dotyczące drzewa decyzyjnego, patrząc na powyższy obrazek:

• Węzeł główny reprezentuje całą populację lub próbkę. Jest on dalej dzielony na dwa lub więcej jednorodnych zbiorów.

• Podział to proces dzielenia węzła na dwa lub więcej węzłów podrzędnych.

• Gdy węzeł podrzędny dzieli się na dalsze węzły podrzędne, nazywany jest węzłem decyzyjnym.

• Węzeł, który nie ulega podziałowi nazywany jest węzłem końcowym lub liściem.

• Gdy usuwamy węzły podrzędne węzła decyzyjnego, proces ten nazywamy przycinaniem. Przeciwieństwem przycinania jest Rozdzielanie.

• Podsekcja całego drzewa jest nazywana Gałęzią.

• Węzeł, który jest podzielony na węzły podrzędne, jest nazywany węzłem nadrzędnym węzłów podrzędnych; natomiast węzły podrzędne są nazywane dziećmi węzła nadrzędnego.

Typy drzew decyzyjnych

Drzewa regresyjne

Przyjrzyjrzyjmy się poniższemu obrazowi, który pomaga zwizualizować naturę podziału przeprowadzanego przez drzewo regresyjne. To pokazuje nieprzycięte drzewo i drzewo regresji dopasowane do losowego zestawu danych. Obie wizualizacje pokazują serię reguł podziału, zaczynając od wierzchołka drzewa. Zauważ, że każdy podział dziedziny jest wyrównany do jednej z osi cech. Koncepcja równoległego podziału na osie uogólnia się w prosty sposób na wymiary większe niż dwa. Dla przestrzeni cech o rozmiarze $p$, będącej podzbiorem $mathbb{R}^p$, przestrzeń ta jest podzielona na $M$ regionów, $R_{m}$, z których każdy jest $p$-wymiarowym „hiperblokiem”.

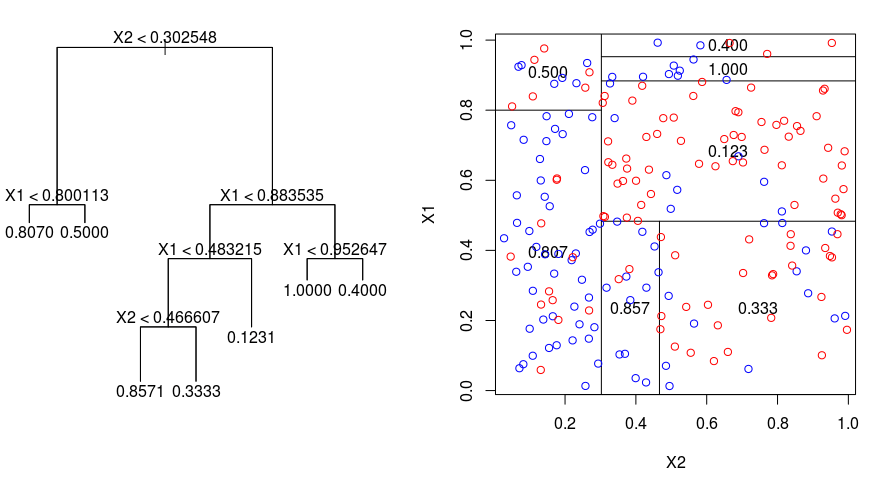
Aby zbudować drzewo regresji, najpierw używamy rekurencyjnego podziału binarnego (ang. recursive binary splititng), aby urosło duże drzewo na danych treningowych, zatrzymując się tylko wtedy, gdy każdy węzeł końcowy ma mniej niż pewną minimalną liczbę obserwacji. Rekursywny podział binarny jest zachłannym algorytmem typu top-down służącym do minimalizacji resztowej sumy kwadratów (RSS), miary błędu stosowanej również w regresji liniowej. RSS, w przypadku partycjonowanej przestrzeni cech z M partycjami, jest dany przez:

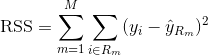
Zaczynając od wierzchołka drzewa, dzielimy je na 2 gałęzie, tworząc partycję 2 przestrzeni. Następnie przeprowadzasz ten konkretny podział na szczycie drzewa wiele razy i wybierasz podział cech, który minimalizuje (bieżący) RSS.

Następnie stosujesz przycinanie złożoności kosztowej do dużego drzewa w celu uzyskania sekwencji najlepszych poddrzew, jako funkcji $alfa$. Podstawową ideą jest wprowadzenie dodatkowego parametru, oznaczonego przez $alfa$, który równoważy głębokość drzewa i jego dobre dopasowanie do danych treningowych.

Możesz użyć K-krotnej walidacji krzyżowej, aby wybrać $alfa$. Ta technika po prostu polega na podzieleniu obserwacji szkoleniowych na K fałd, aby oszacować poziom błędu testowego drzew cząstkowych. Twoim celem jest wybranie tego, który prowadzi do najniższej stopy błędu.

Drzewa klasyfikacyjne

Drzewo klasyfikacyjne jest bardzo podobne do drzewa regresji, z wyjątkiem tego, że jest używane do przewidywania odpowiedzi jakościowej, a nie ilościowej.

Przypomnij, że dla drzewa regresji, przewidywana odpowiedź dla obserwacji jest podana przez średnią odpowiedź obserwacji szkoleniowych, które należą do tego samego węzła końcowego. W przeciwieństwie do tego, dla drzewa klasyfikacyjnego, przewidujesz, że każda obserwacja należy do najczęściej występującej klasy obserwacji szkoleniowych w regionie, do którego należy.

Interpretując wyniki drzewa klasyfikacyjnego, często jesteś zainteresowany nie tylko przewidywaniem klasy odpowiadającej konkretnemu regionowi węzła końcowego, ale także proporcjami klas wśród obserwacji szkoleniowych, które należą do tego regionu.

Zadanie wzrostu drzewa klasyfikacyjnego jest dość podobne do zadania wzrostu drzewa regresji. Podobnie jak w przypadku regresji, używamy rekurencyjnego podziału binarnego, aby wyhodować drzewo klasyfikacyjne. Jednakże, w przypadku klasyfikacji, Resztkowa Suma Kwadratów nie może być użyta jako kryterium podziału binarnego. Zamiast tego można użyć jednej z 3 poniższych metod:

• Współczynnik błędu klasyfikacji: Zamiast obserwować, jak daleko odpowiedź liczbowa jest oddalona od wartości średniej, jak w ustawieniu regresji, można zamiast tego zdefiniować „współczynnik trafienia” jako ułamek obserwacji szkoleniowych w danym regionie, które nie należą do najczęściej występującej klasy. Błąd jest określony równaniem:

E = 1 – argmaxc($hat{pi}_{mc}$)

w którym $hat{pi}_{mc}$ reprezentuje ułamek danych treningowych w regionie Rm, które należą do klasy c.

• Współczynnik Giniego: Indeks Giniego jest alternatywną metryką błędu, która ma za zadanie pokazać, jak „czysty” jest dany region. „Czystość” w tym przypadku oznacza, jak duża część danych treningowych w danym regionie należy do jednej klasy. Jeśli region Rm zawiera dane, które w większości należą do jednej klasy c, wówczas wartość indeksu Giniego będzie mała:

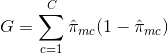
• Intropia krzyżowa: Trzecia alternatywa, która jest podobna do indeksu Giniego, znana jest jako entropia krzyżowa lub dewiancja:

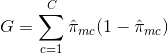
ENTROPIA KRZYŻOWA przyjmie wartość bliską zeru, jeśli wartości $hat{pi}_{mc}$ są wszystkie bliskie 0 lub bliskie 1. Dlatego, podobnie jak indeks Giniego, entropia krzyżowa przyjmie małą wartość, jeśli m-ty węzeł jest czysty. W rzeczywistości okazuje się, że indeks Giniego i entropia krzyżowa są dość podobne liczbowo.

Podczas budowania drzewa klasyfikacyjnego, indeks Giniego lub entropia krzyżowa są zwykle używane do oceny jakości danego podziału, ponieważ są bardziej wrażliwe na czystość węzłów niż współczynnik błędu klasyfikacji. Każde z tych 3 podejść może być użyte podczas przycinania drzewa, ale wskaźnik błędu klasyfikacji jest preferowany, jeśli celem jest dokładność przewidywania ostatecznego przyciętego drzewa.

Wady i zalety drzew decyzyjnych

Główną zaletą używania drzew decyzyjnych jest to, że są one intuicyjnie bardzo łatwe do wyjaśnienia. W porównaniu z innymi podejściami do regresji i klasyfikacji, ściśle odzwierciedlają podejmowanie decyzji przez człowieka. Mogą być wyświetlane graficznie i mogą łatwo obsługiwać jakościowe predyktory bez potrzeby tworzenia zmiennych dummy.

Jednakże drzewa decyzyjne generalnie nie mają tego samego poziomu dokładności predykcyjnej, co inne podejścia, ponieważ nie są całkiem odporne. Mała zmiana w danych może spowodować dużą zmianę w ostatecznie oszacowanym drzewie.

Poprzez agregację wielu drzew decyzyjnych, przy użyciu metod takich jak bagging, lasy losowe i boosting, wydajność predykcyjna drzew decyzyjnych może zostać znacznie poprawiona.

Metody oparte na drzewach

Torowanie

Drzewa decyzyjne omówione powyżej cierpią z powodu wysokiej wariancji, co oznacza, że jeśli podzielisz dane szkoleniowe na 2 części w sposób losowy i dopasujesz drzewo decyzyjne do obu połówek, wyniki, które otrzymasz mogą być zupełnie inne. W przeciwieństwie do tego, procedura z niską wariancją przyniesie podobne wyniki, jeśli zostanie zastosowana wielokrotnie do różnych zbiorów danych.

Bagging, lub agregacja bootstrap, jest techniką używaną do zmniejszenia wariancji przewidywań poprzez połączenie wyników wielu klasyfikatorów modelowanych na różnych podpróbkach tego samego zbioru danych. Oto równanie dla baggingu:

w którym generujesz $B$ różnych bootstrapowanych zestawów danych treningowych. Następnie trenujesz swoją metodę na $b-tym$ bootstrapowanym zestawie treningowym w celu uzyskania $hat{f}_{b}(x)$, a na koniec uśredniasz przewidywania.

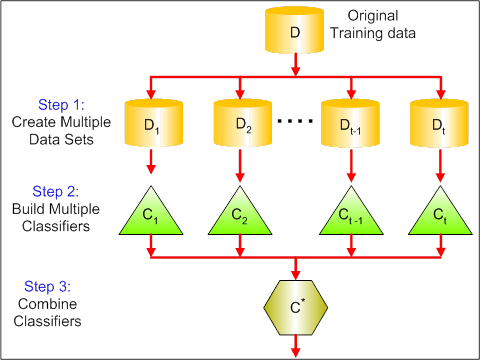
Poniższa wizualizacja pokazuje 3 różne kroki w baggingu:

• Krok 1: Tutaj zastępujesz oryginalne dane nowymi danymi. Nowe dane mają zazwyczaj ułamek kolumn i wierszy danych oryginalnych, które następnie mogą być użyte jako hiperparametry w modelu baggingowym.

• Krok 2: Budujesz klasyfikatory na każdym zbiorze danych. Ogólnie rzecz biorąc, możesz użyć tego samego klasyfikatora do tworzenia modeli i przewidywań.

• Krok 3: Na koniec używasz średniej wartości, aby połączyć przewidywania wszystkich klasyfikatorów, w zależności od problemu. Ogólnie rzecz biorąc, te połączone wartości są bardziej odporne niż pojedynczy model.

Choć workowanie może poprawić przewidywania dla wielu metod regresji i klasyfikacji, jest ono szczególnie przydatne dla drzew decyzyjnych. Aby zastosować workowanie do drzew regresji/klasyfikacji, po prostu konstruujesz $B$ drzew regresji/klasyfikacji używając $B$ bootstrapowanych zestawów treningowych, i uśredniasz wynikowe przewidywania. Drzewa te są hodowane głęboko i nie są przycinane. Stąd każde pojedyncze drzewo ma wysoką wariancję, ale niską skośność. Uśrednianie tych $B$ drzew zmniejsza wariancję.

Powszechnie mówiąc, baggowanie zostało wykazane, aby dać imponującą poprawę dokładności poprzez łączenie razem setek lub nawet tysięcy drzew w jedną procedurę.

Lasy losowe

Lasy losowe to uniwersalna metoda uczenia maszynowego zdolna do wykonywania zarówno zadań regresji jak i klasyfikacji. Podejmuje również metody redukcji wymiarów, traktuje brakujące wartości, wartości odstające i inne istotne kroki eksploracji danych, i wykonuje całkiem dobrą pracę.

Lasy losowe zapewniają poprawę w stosunku do drzew w workach dzięki małej poprawce, która dekoruje drzewa. Podobnie jak w przypadku baggingu, budujesz pewną liczbę drzew decyzyjnych na bootstrapowanych próbkach treningowych. Ale podczas budowania tych drzew decyzyjnych, za każdym razem, gdy rozważany jest podział drzewa, losowa próbka m predyktorów jest wybierana jako kandydaci do podziału z pełnego zestawu $p$ predyktorów. Podział może wykorzystywać tylko jeden z tych $m$ predyktorów. Jest to główna różnica między lasami losowymi a workowaniem; ponieważ tak jak w bagowaniu, wybór predyktora $m = p$.

Aby wyhodować las losowy, powinieneś:

• Najpierw założyć, że liczba przypadków w zbiorze treningowym wynosi K. Następnie pobrać losową próbkę z tych K przypadków, a potem użyć tej próbki jako zbioru treningowego do wzrostu drzewa.

• Jeśli istnieje $p$ zmiennych wejściowych, określić liczbę $m < p$ taką, że w każdym węźle można wybrać $m$ zmiennych losowych spośród $p$. Najlepszy podział na te $m$ jest używany do podziału węzła.

• Każde drzewo jest następnie powiększane do największego możliwego zakresu i nie jest potrzebne przycinanie.

• Na koniec, agreguj przewidywania drzew docelowych, aby przewidzieć nowe dane.

Lasy losowe są bardzo skuteczne w szacowaniu brakujących danych i utrzymywaniu dokładności, gdy brakuje dużej części danych. Może również zrównoważyć błędy w zestawach danych, w których klasy są niezrównoważone. Co najważniejsze, może obsługiwać masywne zbiory danych o dużej wymiarowości. Jednakże, jedną z wad używania Lasów Losowych jest to, że można łatwo przepasować hałaśliwe zbiory danych, szczególnie w przypadku regresji.

Boosting

Boosting jest innym podejściem do poprawy przewidywań wynikających z drzewa decyzyjnego. Podobnie jak bagging i lasy losowe, jest to ogólne podejście, które może być stosowane do wielu metod uczenia statystycznego dla regresji lub klasyfikacji. Przypomnijmy, że bagging polega na tworzeniu wielu kopii oryginalnego zbioru danych treningowych przy użyciu bootstrapu, dopasowując oddzielne drzewo decyzyjne do każdej kopii, a następnie łącząc wszystkie drzewa w celu utworzenia pojedynczego modelu predykcyjnego. W szczególności, każde drzewo jest budowane na bootstrapowanym zbiorze danych, niezależnie od innych drzew.

Boosting działa w podobny sposób, z wyjątkiem tego, że drzewa są uprawiane sekwencyjnie: każde drzewo jest uprawiane przy użyciu informacji z poprzednio uprawianych drzew. Boosting nie obejmuje próbkowania bootstrapowego; zamiast tego każde drzewo jest dopasowywane na zmodyfikowanej wersji oryginalnego zbioru danych.

Dla drzew regresyjnych i klasyfikacyjnych, boosting działa w następujący sposób:

• W przeciwieństwie do dopasowywania pojedynczego dużego drzewa decyzyjnego do danych, co jest równoznaczne z mocnym dopasowaniem do danych i potencjalnym przepasaniem, podejście boostingowe zamiast tego uczy się powoli.

• Dając bieżący model, dopasowujesz drzewo decyzyjne do reszt z modelu. To znaczy, dopasowujesz drzewo używając bieżących reszt, a nie wyniku $Y$, jako odpowiedzi.

• Następnie dodajesz to nowe drzewo decyzyjne do dopasowanej funkcji w celu aktualizacji reszt. Każde z tych drzew może być raczej małe, z zaledwie kilkoma węzłami końcowymi, określanymi przez parametr $d$ w algorytmie. Dopasowując małe drzewa do reszt, powoli poprawiasz $hat{f}$ w obszarach, w których nie radzi sobie dobrze.

• Parametr kurczenia $nu$ jeszcze bardziej spowalnia proces, pozwalając większej liczbie i różnie ukształtowanych drzew zaatakować reszty.

Boosting jest bardzo przydatny, gdy masz dużo danych i spodziewasz się, że drzewa decyzyjne będą bardzo złożone. Boosting został wykorzystany do rozwiązania wielu trudnych problemów klasyfikacji i regresji, w tym analizy ryzyka, analizy sentymentu, reklamy predykcyjnej, modelowania cen, szacowania sprzedaży i diagnozowania pacjentów, między innymi.

Decision Trees in R

Classification Trees

W tej części pracujemy ze zbiorem danych Carseats przy użyciu pakietu tree w R. Należy pamiętać, że najpierw należy zainstalować pakiety ISLR i tree w środowisku R Studio. Załadujmy najpierw ramkę danych Carseats z pakietu ISLR.

library(ISLR)data(package="ISLR")carseats<-Carseats

Załadujmy również pakiet tree.

require(tree)

Zestaw danych Carseats to ramka danych z 400 obserwacjami dotyczącymi następujących 11 zmiennych:

• Sprzedaż: sprzedaż jednostkowa w tysiącach

• CompPrice: cena pobierana przez konkurenta w każdej lokalizacji

• Income: poziom dochodu społeczności w tysiącach dolarów

• Advertising: lokalny budżet reklamowy w każdej lokalizacji w tys. dolarów

• Populacja: regionalna populacja w tysiącach

• Cena: cena za foteliki samochodowe w każdej lokalizacji

• ShelveLoc: Bad, Good lub Medium wskazuje jakość lokalizacji półek

• Age: poziom wieku mieszkańców

• Education: poziom wykształcenia w danej lokalizacji

• Urban: Yes/No

• USA: Yes/No

names(carseats)

Przyjrzyjrzyjmy się histogramowi sprzedaży samochodów:

hist(carseats$Sales)

Zauważmy, że Sales jest zmienną ilościową. Chcesz to zademonstrować za pomocą drzew z odpowiedzią binarną. Aby to zrobić, zamieniasz Sales na zmienną binarną, która będzie się nazywać High. Jeśli sprzedaż jest mniejsza niż 8, nie będzie wysoka. W przeciwnym razie, będzie wysoka. Następnie możesz umieścić tę nową zmienną High z powrotem w ramce danych.

High = ifelse(carseats$Sales<=8, "No", "Yes")carseats = data.frame(carseats, High)

Teraz wypełnijmy model za pomocą drzew decyzyjnych. Oczywiście nie możesz mieć tutaj zmiennej Sales, ponieważ twoja zmienna odpowiedzi High została utworzona z Sales. Tak więc wykluczmy ją i dopasujmy drzewo.

tree.carseats = tree(High~.-Sales, data=carseats)

Zobaczmy podsumowanie twojego drzewa klasyfikacyjnego:

summary(tree.carseats)

Możesz zobaczyć zaangażowane zmienne, liczbę węzłów końcowych, średnią odchylenie resztkowe, a także współczynnik błędu błędnej klasyfikacji. Aby uczynić to bardziej wizualnym, wykreślmy również drzewo, a następnie opatrzmy je adnotacjami za pomocą poręcznej funkcji text:

plot(tree.carseats)text(tree.carseats, pretty = 0)

Jest tak wiele zmiennych, co sprawia, że spojrzenie na drzewo jest bardzo skomplikowane. Przynajmniej można zauważyć, że w każdym z węzłów końcowych są one oznaczone jako Yes lub No. Przy każdym węźle dzielenia są pokazane zmienne i wartość wyboru dzielenia (na przykład Price < 92.5 lub Advertising < 13.5).

Aby uzyskać szczegółowe podsumowanie drzewa, wystarczy je wydrukować. Będzie to przydatne, jeśli będziesz chciał wyciągnąć szczegóły z drzewa do innych celów:

tree.carseats

Nadszedł czas, aby przyciąć drzewo. Utwórzmy zestaw treningowy i testowy, dzieląc ramkę danych carseats na 250 próbek treningowych i 150 testowych. Najpierw ustawiamy ziarno, aby wyniki były powtarzalne. Następnie pobieramy losową próbkę numerów ID (indeksów) próbek. Konkretnie tutaj, próbkujesz z zestawu od 1 do n liczba rzędów siedzeń samochodowych, która wynosi 400. Chcesz mieć próbkę o rozmiarze 250 (domyślnie próbka używa bez zastępowania).

set.seed(101)train=sample(1:nrow(carseats), 250)

Więc teraz otrzymujesz ten indeks train, który indeksuje 250 z 400 obserwacji. Możesz ponownie dopasować model z tree, używając tej samej formuły, z wyjątkiem powiedzenia drzewu, aby użyło podzbioru równego train. Następnie wykonajmy wykres:

tree.carseats = tree(High~.-Sales, carseats, subset=train)plot(tree.carseats)text(tree.carseats, pretty=0)

Wygląd wykresu jest nieco inny z powodu nieco innego zestawu danych. Niemniej jednak złożoność drzewa wygląda mniej więcej tak samo.

Teraz zamierzasz wziąć to drzewo i przewidzieć je na zestawie testowym, używając metody predict dla drzew. Tutaj będziesz chciał faktycznie przewidzieć etykiety class.

tree.pred = predict(tree.carseats, carseats, type="class")

Wtedy możesz ocenić błąd za pomocą tabeli błędnej klasyfikacji.

with(carseats, table(tree.pred, High))

Na przekątnych są poprawne klasyfikacje, podczas gdy poza przekątnymi są błędne. Chcesz przywrócić tylko te poprawne. Aby to zrobić, możesz wziąć sumę 2 przekątnych podzieloną przez całość (150 obserwacji testowych).

(72 + 43) / 150

Ok, otrzymujesz błąd 0,76 z tym drzewem.

Podczas hodowania dużego, krzaczastego drzewa, może ono mieć zbyt dużą wariancję. Tak więc, użyjmy walidacji krzyżowej, aby przyciąć drzewo optymalnie. Używając cv.tree, użyjesz błędu błędnej klasyfikacji jako podstawy do wykonania przycinania.

cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)cv.carseats

Wydrukowanie wyników pokazuje szczegóły ścieżki walidacji krzyżowej. Można zobaczyć rozmiary drzew, które były przycinane z powrotem, odchylenia w miarę przycinania, a także parametr złożoności kosztów używany w procesie.

Wykreślmy to:

plot(cv.carseats)

Patrząc na wykres, widać część spirali w dół z powodu błędu klasyfikacji na 250 punktach walidacji krzyżowej. Więc wybierzmy wartość w krokach w dół (12). Następnie przycinajmy drzewo do rozmiaru 12, aby zidentyfikować to drzewo. Wreszcie, wykreślmy i opatrzmy adnotacją to drzewo, aby zobaczyć wynik.

prune.carseats = prune.misclass(tree.carseats, best = 12)plot(prune.carseats)text(prune.carseats, pretty=0)

Jest nieco płytsze niż poprzednie drzewa i można faktycznie odczytać etykiety. Oceńmy to ponownie na zestawie danych testowych.

tree.pred = predict(prune.carseats, carseats, type="class")with(carseats, table(tree.pred, High))

(74 + 39) / 150

Wygląda na to, że poprawne klasyfikacje trochę spadły. Zrobiło to mniej więcej to samo, co twoje oryginalne drzewo, więc przycinanie nie zaszkodziło zbytnio w odniesieniu do błędów błędnej klasyfikacji i dało prostsze drzewo.

Często zdarza się, że drzewa nie dają bardzo dobrych błędów predykcji, więc przyjrzyjmy się lasom losowym i boostingowi, które mają tendencję do przewyższania drzew pod względem błędów predykcji i błędnej klasyfikacji.

Lasy losowe

W tej części użyjesz zbioru Boston housing data do zbadania lasów losowych i boostingu. Zbiór danych znajduje się w pakiecie MASS. Podaje on wartości mieszkaniowe i inne statystyki w każdym z 506 przedmieść Bostonu na podstawie spisu powszechnego z 1970 roku.

library(MASS)data(package="MASS")boston<-Bostondim(boston)names(boston)

Załadujmy również pakiet randomForest.

require(randomForest)

Aby przygotować dane dla lasu losowego, ustawmy ziarno i stwórzmy przykładowy zbiór treningowy składający się z 300 obserwacji.

set.seed(101)train = sample(1:nrow(boston), 300)

W tym zbiorze danych znajduje się 506 przedmieść Bostonu. Dla każdego surburb masz zmienne, takie jak przestępczość na mieszkańca, rodzaje przemysłu, średni # pokoi na mieszkanie, średnia proporcja wieku domów itp. Użyjmy medv – mediany wartości domów zamieszkanych przez właścicieli dla każdego z tych surburbs, jako zmiennej odpowiedzi.

Dopasujmy las losowy i zobaczmy, jak dobrze działa. Jak już zostało powiedziane, używasz odpowiedzi medv, mediany wartości mieszkaniowej (w dolarach $1K) i zestawu próbek szkoleniowych.

rf.boston = randomForest(medv~., data = boston, subset = train)rf.boston

Wydrukowanie lasu losowego daje jego podsumowanie: # drzew (500 zostało wyhodowanych), średnie kwadraty reszt (MSR) i procent wyjaśnionej wariancji. MSR i % wariancji wyjaśnionej są oparte na szacunkach poza workiem, bardzo sprytnym urządzeniu w lasach losowych, aby uzyskać uczciwe szacunki błędów.

Jedynym parametrem dostrajania w lasach losowych jest argument o nazwie mtry, który jest liczbą zmiennych, które są wybierane przy każdym podziale każdego drzewa, gdy dokonujesz podziału. Jak widać tutaj, mtry to 4 z 13 zmiennych eksploracyjnych (z wyłączeniem medv) w danych Boston Housing – co oznacza, że za każdym razem, gdy drzewo przychodzi do podziału węzła, 4 zmienne byłyby wybierane losowo, a następnie podział byłby ograniczony do 1 z tych 4 zmiennych. W ten sposób randomForests de-koreluje drzewa.

Zamierzasz dopasować serię lasów losowych. Jest 13 zmiennych, więc niech mtry ma zakres od 1 do 13:

• Aby zarejestrować błędy, ustawiasz 2 zmienne oob.err i test.err.

• W pętli mtry od 1 do 13, najpierw dopasowujesz randomForest z tą wartością mtry na zbiorze danych train, ograniczając liczbę drzew do 350.

• Potem wyciągasz średni błąd kwadratowy na obiekcie (błąd out-of-bag).

• Potem przewidujesz na zbiorze danych testowych (boston) używając fit (dopasowanie randomForest).

• Na koniec obliczasz błąd testu: błąd średniokwadratowy, który jest równy mean( (medv - pred) ^ 2 ).

oob.err = double(13)test.err = double(13)for(mtry in 1:13){ fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350) oob.err = fit$mse pred = predict(fit, boston) test.err = with(boston, mean( (medv-pred)^2 ))}

W zasadzie właśnie wyhodowałeś 4550 drzew (13 razy 350). Zróbmy teraz wykres za pomocą polecenia matplot. Błąd testu i błąd poza workiem są połączone razem, aby utworzyć dwukolumnową macierz. W macierzy jest jeszcze kilka innych argumentów, w tym wartości znaków wykresu (pch = 23 oznacza wypełniony diament), kolory (czerwony i niebieski), type equals both (wykres obu punktów i połączenie ich liniami) oraz nazwa osi y (Mean Squared Error). Możesz również umieścić legendę w prawym górnym rogu działki.

matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))

Idealnie, te 2 krzywe powinny się pokrywać, ale wydaje się, że błąd testu jest nieco niższy. Istnieje jednak duża zmienność w tych szacunkach błędu testu. Ponieważ oszacowanie błędu out-of-bag zostało obliczone na jednym zestawie danych, a oszacowanie błędu testu zostało obliczone na innym zestawie danych, te różnice są dość dobrze w granicach błędów standardowych.

Zauważ, że czerwona krzywa jest płynnie powyżej niebieskiej krzywej? Te oszacowania błędów są bardzo skorelowane, ponieważ randomForest z mtry = 4 jest bardzo podobny do tego z mtry = 5. Dlatego każda z tych krzywych jest dość gładka. To, co widzisz, to fakt, że mtry wokół 4 wydaje się być najbardziej optymalnym wyborem, przynajmniej dla błędu testowego. Ta wartość mtry dla błędu out-of-bag równa się 9.

Tak więc przy bardzo niewielu warstwach dopasowałeś bardzo potężny model predykcyjny przy użyciu lasów losowych. Jak to możliwe? Po lewej stronie pokazana jest wydajność pojedynczego drzewa. Średni błąd kwadratowy na out-of-bag wynosi 26, a ty spadłeś do około 15 (nieco powyżej połowy). Oznacza to, że zmniejszyłeś błąd o połowę. Podobnie w przypadku błędu testu, zmniejszyłeś błąd z 20 do 12.

Boosting

W porównaniu z lasami losowymi, boosting tworzy mniejsze i bardziej uparte drzewa, a także idzie na skróty. Będziesz używał pakietu GBM (Gradient Boosted Modeling), w R.

require(gbm)

GBM pyta o rozkład, który jest gaussowski, ponieważ będziesz robił stratę kwadratu błędu. Poprosisz GBM o 10,000 drzew, co brzmi jak dużo, ale będą to płytkie drzewa. Głębokość interakcji to liczba podziałów, więc chcesz mieć 4 podziały w każdym drzewie. Shrinkage to 0.01, czyli jak bardzo zmniejszysz krok drzewa do tyłu.

boost.boston = gbm(medv~., data = boston, distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)summary(boost.boston)

Funkcja summary daje wykres ważności zmiennych. Wygląda na to, że są 2 zmienne, które mają wysoką względną ważność: rm (liczba pokoi) i lstat (odsetek osób o niższym statusie ekonomicznym w społeczności). Wykreślmy te 2 zmienne:

plot(boost.boston,i="lstat")plot(boost.boston,i="rm")

Pierwszy wykres pokazuje, że im wyższy odsetek osób o niższym statusie ekonomicznym na przedmieściach, tym niższa wartość cen mieszkań. Drugi wykres pokazuje odwrotną zależność z liczbą pokoi: średnia liczba pokoi w domu rośnie wraz ze wzrostem ceny.

Czas przewidzieć model wzmocniony na zbiorze danych testowych. Przyjrzyjmy się wydajności testu w funkcji liczby drzew:

• Najpierw tworzysz siatkę liczby drzew w krokach co 100 od 100 do 10 000.

• Następnie uruchamiasz funkcję predict na modelu boosted. Przyjmuje ona n.trees jako argument i tworzy macierz predykcji na danych testowych.

• Wymiary macierzy to 206 obserwacji testowych i 100 różnych wektorów predykcji przy 100 różnych wartościach drzewa.

  n.trees = seq(from = 100, to = 10000, by = 100)predmat = predict(boost.boston, newdata = boston, n.trees = n.trees)dim(predmat)

Czas obliczyć błąd testowy dla każdego z wektorów predykcji:

• predmat jest macierzą, medv jest wektorem, zatem (predmat – medv) jest macierzą różnic. Możesz użyć funkcji apply do kolumn tych kwadratowych różnic (średnia). To obliczyłoby kolumnowo średni błąd kwadratowy dla wektorów predykcyjnych.

• Następnie wykonujesz wykres przy użyciu podobnych parametrów do tego, który jest używany dla Random Forest. Pokazałby on wykres błędu boostingu.

  boost.err = with(boston, apply( (predmat - medv)^2, 2, mean) )plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")abline(h = min(test.err), col = "red")

Błąd boostingu dość znacznie spada wraz ze wzrostem liczby drzew. Jest to dowód na to, że boosting jest niechętny do nadmiernego dopasowania. Włączmy również najlepszy błąd testowy z randomForest do wykresu. Boostowanie faktycznie dostaje rozsądną ilość poniżej błędu testowego dla randomForest.

Wnioski

Więc to już koniec tego tutorialu w R na temat budowania modeli drzew decyzyjnych: drzew klasyfikacyjnych, lasów losowych i drzew boostowanych. Te 2 ostatnie są potężnymi metodami, których możesz użyć w każdej chwili, gdy zajdzie taka potrzeba. Z mojego doświadczenia wynika, że boosting zazwyczaj przewyższa RandomForest, ale RandomForest jest łatwiejszy do zaimplementowania. W RandomForest, jedynym parametrem dostrajania jest liczba drzew; podczas gdy w boostingu, więcej parametrów dostrajania jest wymaganych poza liczbą drzew, w tym kurczenie i głębokość interakcji.

Jeśli chcesz dowiedzieć się więcej, upewnij się, że spojrzysz na nasz kurs Machine Learning Toolbox dla R.

.