Logistic Regression - The Ultimate Beginners Guide

Logistic Regression Equation
Logistic Regression Example Curves
Logistic Regression – B-Coefficients
Logistic Regression – Effect Size
Logistic Regression Assumptions

Logistic regression is a technique for predicting a
dichotomous outcome variable from 1+ predictors.Przykład: jak prawdopodobne jest, że ludzie umrą przed 2020 rokiem, biorąc pod uwagę ich wiek w 2015 roku? Zauważ, że „umrzeć” jest zmienną dychotomiczną, ponieważ ma tylko 2 możliwe wyniki (tak lub nie).
Ta analiza jest również znana jako binarna regresja logistyczna lub po prostu „regresja logistyczna”. Powiązaną techniką jest wielomianowa regresja logistyczna, która przewiduje zmienne wynikowe z 3+ kategoriami.

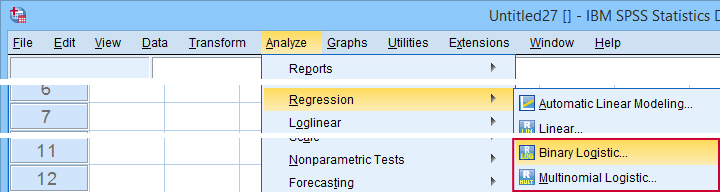
Regresja logistyczna – prosty przykład

Dom opieki posiada dane na temat płci N = 284 klientów, wieku w dniu 1 stycznia 2015 r. i czy klient zmarł przed 1 stycznia 2020 r. Surowe dane znajdują się w tym arkuszu Googlesheet, częściowo pokazane poniżej.

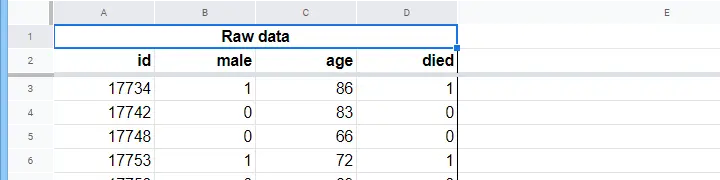
Skupmy się najpierw na wieku: czy możemy przewidzieć śmierć przed 2020 rokiem na podstawie wieku w 2015 roku? A jeśli tak, to jak dokładnie? I w jakim stopniu? Dobrym pierwszym krokiem jest sprawdzenie wykresu rozrzutu, takiego jak pokazany poniżej.

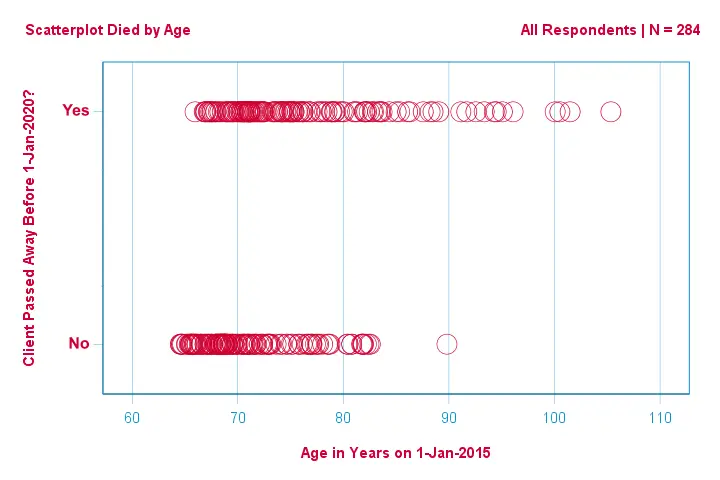
Kilka rzeczy, które widzimy na tym wykresie rozrzutu, to to, że

wszyscy oprócz jednego klienta w wieku powyżej 83 lat zmarli w ciągu następnych 5 lat;
odchylenie standardowe wieku jest znacznie większe dla klientów, którzy zmarli, niż dla klientów, którzy przeżyli;
wiek ma znaczną dodatnią skośność, szczególnie dla klientów, którzy zmarli.

Ale jak możemy przewidzieć, czy klient umarł, biorąc pod uwagę jego wiek? Zrobimy to właśnie poprzez dopasowanie krzywej logistycznej.

Proste równanie regresji logistycznej

Prosta regresja logistyczna oblicza prawdopodobieństwo jakiegoś wyniku przy pojedynczej zmiennej przewidującej jako

$P(Y_i) = \frac{1}{1 + e^{,

(e) jest stałą matematyczną o przybliżonej wartości 2.72;

(b_0} to stała oszacowana na podstawie danych;

(b_1} to współczynnik b oszacowany na podstawie danych;

(X_i} to zaobserwowany wynik zmiennej $X$ dla przypadku \(i).

Istotą regresji logistycznej jest oszacowanie współczynnika $b_0$ i $b_1$. Te dwie liczby pozwalają nam obliczyć prawdopodobieństwo śmierci klienta przy dowolnym zaobserwowanym wieku. Zilustrujemy to za pomocą kilku przykładowych krzywych, które dodaliśmy do poprzedniego wykresu rozrzutu.

Przykładowe krzywe regresji logistycznej

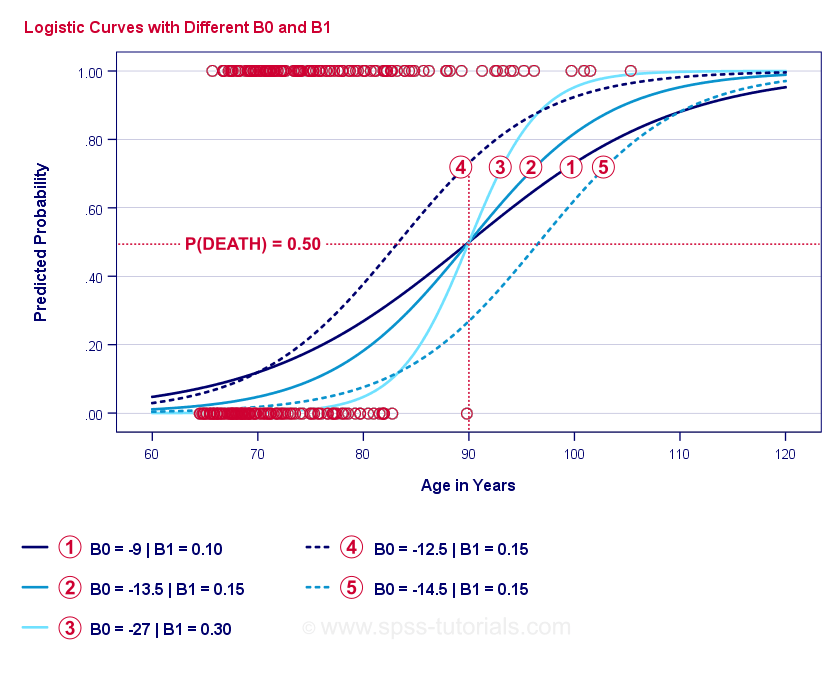
Jeśli poświęcisz chwilę na porównanie tych krzywych, możesz zauważyć, co następuje:

∗ określa poziome położenie krzywych: wraz ze wzrostem ∗ krzywe przesuwają się w lewo, ale ich stromość pozostaje niezmieniona. Widać to dla krzywych , i . Zauważmy, że $b_0$ jest różne, ale $b_1$ jest równe dla tych krzywych. Krzywe i przewidują w przybliżeniu 0,50 i 0,25 prawdopodobieństwa śmierci dla 90-letniego klienta.
$b_1$ określa stromość krzywych: jeśli $b_1$ > 0, prawdopodobieństwo śmierci wzrasta wraz z wiekiem. Zależność ta staje się silniejsza, gdy \u2001 \u2001 \u2001 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 Krzywe , i ilustrują ten punkt: wraz ze wzrostem wartości b krzywe stają się bardziej strome, więc prawdopodobieństwo śmierci rośnie szybciej wraz z wiekiem.

Na razie pozostało nam jedno pytanie: jak znaleźć „najlepsze” $b_0$ i $b_1$?

Regresja logistyczna – logiczne prawdopodobieństwo

Dla każdego respondenta model regresji logistycznej szacuje prawdopodobieństwo wystąpienia jakiegoś zdarzenia $Y_i$. Oczywiście, prawdopodobieństwa te powinny być wysokie, jeśli zdarzenie rzeczywiście wystąpiło, i odwrotnie. Jednym ze sposobów podsumowania tego, jak dobrze jakiś model sprawdza się w przypadku wszystkich respondentów, jest log-likelihood $LL$:

$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) ∗ ln(1 – P(Y_i))$$

gdzie

∗(Y_i) wynosi 1, jeśli zdarzenie miało miejsce, a 0, jeśli nie miało miejsca;
∗(ln) oznacza logarytm naturalny: do jakiej potęgi należy podnieść ∗(e), aby otrzymać daną liczbę?

(LL) jest miarą dobroci dopasowania: wszystko inne jest takie samo, model regresji logistycznej lepiej pasuje do danych, o ile ∗(LL) jest większe. Nieco mylące jest to, że ˆ(LL) jest zawsze ujemna. Chcemy więc znaleźć wartości $b_0$ i $b_1$, dla których $LL$ jest tak bliskie zeru, jak to tylko możliwe.

Maximum Likelihood Estimation

W przeciwieństwie do regresji liniowej, regresja logistyczna nie może łatwo obliczyć optymalnych wartości $b_0$ i $b_1$. Zamiast tego musimy próbować różnych liczb, aż do momentu, gdy ˆ(LL) nie będzie dalej wzrastać. Każda taka próba nazywana jest iteracją. Proces znajdowania optymalnych wartości poprzez takie iteracje jest znany jako estymacja maksymalnej wiarygodności.

Więc to jest w zasadzie sposób, w jaki oprogramowanie statystyczne – takie jak SPSS, Stata lub SAS – uzyskuje wyniki regresji logistycznej. Na szczęście są one w tym zadziwiająco dobre. Ale zamiast raportować $LL$, pakiety te raportują $-2LL$. $-2LL$ jest miarą „badness-of-fit”, która podąża za rozkładem
chi-square. To sprawia, że $-2LL$ jest użyteczna do porównywania różnych modeli, jak zobaczymy wkrótce. $-2LL$ jest oznaczana jako -2 Log likelihood w danych wyjściowych pokazanych poniżej.

Przypis tutaj mówi nam, że estymacja maksymalnej wiarygodności potrzebowała tylko 5 iteracji do znalezienia optymalnych współczynników b $b_0$ i $b_1$. Przyjrzyjmy się im teraz.

Regresja logistyczna – Współczynniki B

Najważniejszymi danymi wyjściowymi dla każdej analizy regresji logistycznej są współczynniki b. Poniższy rysunek pokazuje je dla naszych przykładowych danych.

Zanim przejdziemy do szczegółów, dane wyjściowe krótko pokazują

współczynniki b, które tworzą nasz model;
błędy standardowe dla tych współczynników b;
statystykę Walda – obliczaną jako $(\frac{B}{SE})^2$ – która podąża za rozkładem chi kwadrat;
stopnie swobody dla statystyki Walda;
poziomy istotności dla współczynników b;
wykładnicze współczynniki b lub e^B są ilorazami szans związanymi ze zmianami w wynikach predyktora;
95% przedział ufności dla wykładniczych współczynników b.

Współczynniki b uzupełniają nasz model regresji logistycznej, który jest teraz

$P(śmierć_i) = \frac{1}{1 + e^{(-9,079,+,0.079}}}=$$

$P(śmierć_i) = \frac{1}{1 + e^{przyp.tłum, 0.249}}}=$$

$P(śmierć_i) = \frac{1}{1 + 0.780}=$$

$P(śmierć_i) = 0.562$$

Więc teraz wiemy jak przewidzieć śmierć w ciągu 5 lat biorąc pod uwagę czyjś wiek. Ale jak dobra jest ta prognoza? Jest kilka podejść. Zacznijmy od porównania modeli.

Regresja logistyczna – Model bazowy

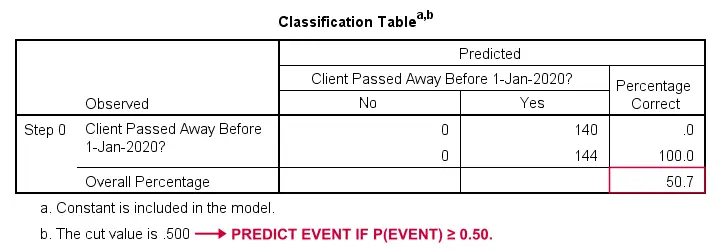
Jak moglibyśmy przewidzieć, kto umarł, gdybyśmy nie mieli żadnych innych informacji? Cóż, 50.7% naszej próbki odeszło. Więc przewidywane prawdopodobieństwo byłoby po prostu 0.507 dla wszystkich.

Dla celów klasyfikacji, zwykle przewidujemy, że zdarzenie ma miejsce jeśli p(zdarzenie) ≥ 0.50. Ponieważ p(zmarł) = 0.507 dla wszystkich, po prostu przewidujemy, że wszyscy odeszli. To przewidywanie jest poprawne dla 50.7% naszej próbki, która zmarła.

Regresja logistyczna – Współczynnik prawdopodobieństwa

Teraz, z tych przewidywanych prawdopodobieństw i obserwowanych wyników możemy obliczyć naszą miarę badness-of-fit: -2LL = 393.65. Nasz rzeczywisty model – przewidywanie śmierci od wieku – wychodzi z -2LL = 354.20. Różnica między tymi liczbami jest znana jako współczynnik prawdopodobieństwa (LR):

$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Ważne jest to, że ∗ LR ma rozkład chi kwadrat z ∗ stopniami swobody, obliczonym jako

$$df = k_{model} – k_{baseline}$$

gdzie k oznacza liczbę parametrów oszacowanych przez modele. Jak pokazano w tym arkuszu Googlesheet, $LR$ i $df$ dają w wyniku poziom istotności dla całego modelu.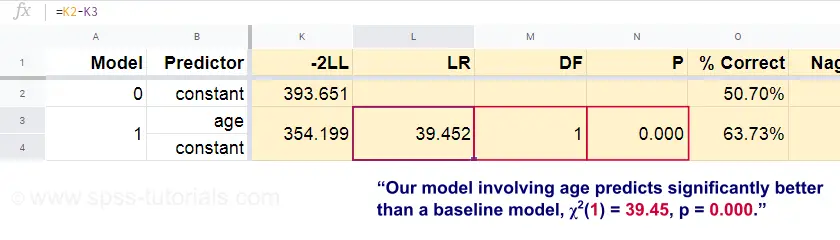

Hipotezą zerową jest tutaj, że jakiś model przewiduje równie słabo jak model bazowy w jakiejś populacji. Ponieważ p = 0,000, odrzucamy ją: nasz model (przewidujący śmierć z powodu wieku) działa znacząco lepiej niż model bazowy bez żadnych predyktorów.
Ale dokładnie o ile lepiej? Na to pytanie odpowiada jego wielkość efektu.

Regresja logistyczna – wielkość efektu modelu

Dobrym sposobem oceny, jak dobrze działa nasz model, jest miara wielkości efektu. Jedną z opcji jest współczynnik Coxa & Snell R2 lub ^(R^2_{CS}) obliczany jako

$R^2_{CS} = 1 – e^{frac{(-2LL_{model})\,(-2LL_{baseline})}{n}}$$

Niestety, ^(R^2_{CS}) nigdy nie osiąga swojego teoretycznego maksimum równego 1. Dlatego często preferowana jest skorygowana wersja znana jako Nagelkerke R2 lub \(R^2_{N}):

$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}}$$

Dla naszych przykładowych danych \(R^2_{CS}}) = 0,130, co wskazuje na średnią wielkość efektu. \(R^2_{N}} = 0,173, nieco większa niż średnia.

Ostatnio, \(R^2_{CS}}) i \(R^2_{N}} są technicznie zupełnie inne niż r-kwadrat obliczany w regresji liniowej. Starają się one jednak spełniać tę samą rolę. Obie miary są zatem znane jako pseudo miary r-kwadratowe.

Regresja logistyczna – wielkość efektu predyktora

Co dziwne, bardzo niewiele podręczników wspomina o jakiejkolwiek wielkości efektu dla poszczególnych predyktorów. Być może dlatego, że są one całkowicie nieobecne w SPSS. Powodem, dla którego ich potrzebujemy, jest to, że współczynniki b zależą od (arbitralnej) skali naszych predyktorów: jeśli wprowadzilibyśmy wiek w dniach zamiast w latach, jego współczynnik b skurczyłby się ogromnie. To oczywiście sprawia, że współczynniki b są nieodpowiednie do porównywania predyktorów w ramach różnych modeli lub pomiędzy nimi.
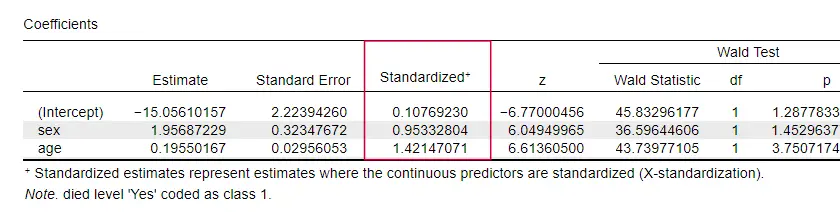
JASP zawiera częściowo znormalizowane współczynniki b: predyktory ilościowe – ale nie zmienna wyniku – są wprowadzane jako współczynniki z, jak pokazano poniżej.

Założenia regresji logistycznej

Analiza regresji logistycznej wymaga następujących założeń:

niezależne obserwacje;
poprawna specyfikacja modelu;
bezbłędny pomiar zmiennej wynikowej i wszystkich predyktorów;
liniowość: każdy predyktor jest liniowo związany z ^B (iloraz szans).

Założenie 4 jest nieco dyskusyjne i pomijane przez wiele podręczników1,6. Można je ocenić za pomocą testu Boxa-Tidwella, omówionego przez Fielda4. To w zasadzie sprowadza się do testowania, czy istnieją jakiekolwiek efekty interakcji między każdym predyktorem a jego logarytmem naturalnym lub LN.

Wielokrotna regresja logistyczna

Dotychczas nasza dyskusja była ograniczona do prostej regresji logistycznej, która wykorzystuje tylko jeden predyktor. Model ten można łatwo rozszerzyć o dodatkowe predyktory, w wyniku czego otrzymujemy wielokrotną regresję logistyczną:

$P(Y_i) = \frac{1}{1 + e^{,(b_0},(b_1X_{1i}+,,b_2X_{2i}+,…+, b_kX_{ki})}}$$