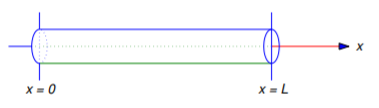
Iniciamos o estudo das equações diferenciais parciais com o problema do fluxo de calor em uma barra uniforme de comprimento, situada no eixo com uma extremidade na origem e a outra no eixo com uma extremidade na origem (Figura 1).
Apesamos que a barra está perfeitamente isolada excepto possivelmente nos seus extremos, e que a temperatura é constante em cada secção transversal e por isso depende apenas de \(x) e \(t). Assumimos também que as propriedades térmicas da barra são independentes da(x) e da(t). Neste caso, pode ser mostrado que a temperatura \(u = u(x, t)\) no momento em que as unidades da origem satisfazem a equação diferencial parcial
onde \(a) é uma constante positiva determinada pelas propriedades térmicas. Esta é a equação de calor.
Começamos com as condições de limite \(u(0,t)=u(L,t)=0\), e escrevemos o problema de valor limite inicial como
>
O nosso método para resolver este problema chama-se separação de variáveis (não confundir com o método de separação de variáveis usado na Secção 2.2 para resolver equações diferenciais ordinárias). Começamos por procurar por funções da forma
que não são identicamente zero e satisfazem
>
> para todas \((x,t)\)). Desde
>(v_t=a^2v_{xx}}} se e só se
>
>
que reescrevemos como
>
Desde que a expressão à esquerda é independente de { x} enquanto que a da direita é independente de { t}, esta equação só se pode manter para todos se os dois lados forem iguais à mesma constante, a que chamamos uma constante de separação, e escrevê-la como lambda; assim,
Isto é equivalente a
>
e
>
Desde \i(v(0),t)=X(0)T(t)=0\) e {\i(v(L,t)=X(L)T(t)=0\i} e não queremos que seja identicamente zero, {\i(X(0)=0\i} e {\i(X(L)=0\i}. Por isso, o problema do valor limite deve ser um valor próprio do problema do valor limite
e o problema do valor próprio deve ser um valor próprio do problema do valor limite
e o problema do valor próprio deve ser um valor próprio do problema do valor limite. De Theorem 11.1.2, os valores próprios da equação {eq:12.1.3} são {lambda_n=n^2\pi^2/L^2\), com funções próprias associadas
Substituindo {lambda=n^2\pi^2/L^2\) na equação {eq:12.1.2}produção
que tem a solução
>
>Agora let
>Desde
>
>
>
(v_n) satisfaz a equação {eq:12.12.1.1} com {f(f(x)=sin n\pi x/L}.
Teorema \\(\PageIndex{1})
A solução formal da inicial…problema do valor limite
é
>
>onde
>
>
>
é a série seno de Fourier em ou seja,
Usamos o termo “solução formal” nesta definição porque não é em geral verdade que a série infinita na Equação {eq:12.1.5} realmente satisfaz todos os requisitos do problema do valor limite inicial da Equação \ef{eq:12.1.4} quando o faz, dizemos que é uma solução real da Equação \ef{eq:12.1.4}.
Por causa dos exponenciais negativos na Equação {eq:12.1.5}, {eq:12.1.5}, a(u) converge para todos os {(x,t)} com {(t>0} (Exercício 12.1.54). Como cada termo na Equação {eq:12.1.5} satisfaz a equação de calor e as condições de limite na Equação {eq:12.1}.4}, também tem estas propriedades se o(u_t) e o(u_xx) puderem ser obtidos diferenciando a série na equação {eq:12.1.5} termo por termo uma vez em relação ao(t) e duas vezes em relação ao(x), para o(t>0). No entanto, nem sempre é legítimo diferenciar um termo em série infinita por termo. O teorema seguinte dá uma condição útil suficiente para legitimar a diferenciação de um termo por termo de uma série infinita. Nós omitimos a prova.
Theorem \\(\PageIndex{2})
Uma série infinita convergente
pode ser diferenciada termo por termo num intervalo fechado para obter
((z=z_1}) e { z=z_2})desde que seja contínuo em M_1 e em 716,\) \(M_2,\) ……, são constantes de tal forma que a série converge.
Theorem {\i}(PageIndex{2}), aplicado duas vezes com { z=x} e uma vez com { z=t}, mostra que {\i}(u_{xx}) e {\i}(u_t}) podem ser obtidos diferenciando termo por termo se {\i}(t>0} (Exercício 12.1.54). Portanto, satisfaz a equação de calor e as condições de contorno na equaçãoref{eq:12.1.4} para {t>0}. Portanto, uma vez que \(u(x,0)=S(x)\) para \(0\le x\le L), \(u) é uma solução real da Equação \ref{eq:12.1.4} se e somente se \(S(x)=f(x)\) para \(0\le x\le L). Do teorema 11.3.2, isto é verdade se a(f) for contínua e parcialmente lisa no \\(f(0)=f(L)=0\).
Neste capítulo, vamos definir soluções formais de vários tipos de problemas. Quando lhe pedimos para resolver tais problemas, queremos sempre dizer que você deve encontrar uma solução formal.
Exemplo \(\PageIndex{1})
Equação de Solução \ref{eq:12.1.4} com \(f(x)=x(x^2-3Lx+2L^2)\).
Solução
De exemplo \\) é
>
Então
Se ambas as extremidades da barra estão isoladas de modo que nenhum calor possa passar por elas, então as condições de contorno são
>
Deixamos isso para você (Exercício 12.1.1) para usar o método de separação de variáveis e Teorema 11.1.3 para motivar a próxima definição.
Teorema \\(\PageIndex{3})
>A solução formal do problema do valor limite inicial
>
é
>
>
>
onde
>
é a série cosina de Fourier de \(f\) em \(;\ou seja,
Exemplo \\(\PageIndex{2})
Equação de Solvente \ref{eq:12.1.6} com {f(x)=x}.
Solução
Do exemplo 11.3.1, a série cosina de Fourier de \\(f\) sobre \(f\) é
>
>Então
>
Deixamos isso para você (Exercício 12.1.2) para usar o método de separação de variáveis e Teorema 11.1.4 para motivar a próxima definição.
Teorema \\(\PageIndex{4})
>A solução formal do problema do valor limite inicial
>
é
>
>
>
onde
é a série senoidal mista de Fourier em \(;\ou seja,
Exemplo \\(\PageIndex{3})
Equação de Solvente \ref{eq:12.1.7} com \(f(x)=x\).
Solução
Do Exemplo 11.3.4, a série senoidal mista de Fourier sobre \\(f\) é
>
>Por isso
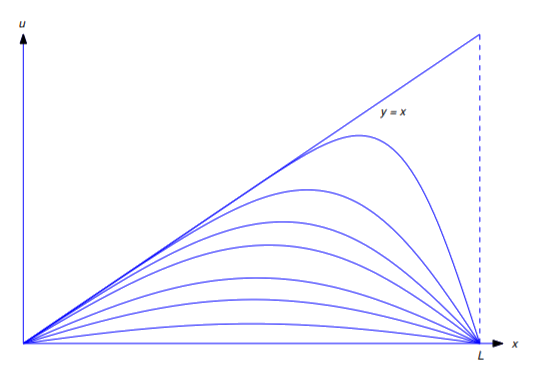
Figure \(\PageIndex{2}) mostra um gráfico de \(u=u(x,t)\) traçado em relação a \(x)=x) para vários valores de \(t)=x. A linha {\i1}(y=x=) corresponde a {\i}(t=0}). As outras curvas correspondem a valores positivos de À medida que \(t\) aumenta, os gráficos aproximam-se da linha \(u=0\).
Deixamos para você (Exercício 12.1.3) a utilização do método de separação de variáveis e Teorema 11.1.5 para motivar a próxima definição.
Teorema \(\PageIndex{5}})
A solução formal da inicial…problema do valor limite
é
>onde
>
>
é a série mista de Fourier cosseno ou seja,
Exemplo \\(\PageIndex{4})
Equação de Solvente \ref{eq:12.1.8} com \(f(x)=x-L\).
Solução
Do Exemplo 11.3.3, a série mista de coseno de Fourier sobre \(f\) é
>
Então
Tecnologia de uso
A experimentos numéricos podem melhorar a sua compreensão das soluções dos problemas de valor limite inicial. Para ser específico, considere a solução formal
da Equação {eq:12.1.4}, onde
é a série senoidal de Fourier de {(f) em {eq:12.1.4}. Considere a soma parcial de {\i1}7816>
Para vários valores fixos de {\i} (incluindo {\i(t=0\i})), gráfico de {\i(u_m(x,t)}) versus {\i(t)}. Em alguns casos pode ser útil fazer um gráfico das curvas correspondentes aos vários valores de \(t) nos mesmos eixos em outros casos você pode querer fazer um gráfico das várias curvas sucessivamente (para aumentar os valores de \(t)), e criar uma figura de movimento primitivo no seu monitor. Repita esta experiência para vários valores de m, para comparar como os resultados dependem dos valores pequenos e grandes de t. Contudo, tenha em mente que os significados de “pequeno” e “grande” neste caso dependem das constantes (a^2) e (L^2). Uma boa maneira de lidar com isto é reescrever a equação {eq:12.1.12} como
>
onde
e o gráfico {eq:12.1.12} para valores selecionados de {a^2}.
Estes comentários também se aplicam às situações consideradas em Teoremas {3}(PageIndex{5})-(PageIndex{5}), exceto que a Equação {eq:12.1.13} deve ser substituída por
em Theorems {\PageIndex{4}} e {\PageIndex{5}.