• Equação de Regressão Lógica
• Curvas de Exemplo de Regressão Lógica
• Regressão Lógica – B-Coefficients
• Regressão logística – Tamanho do efeito
• Premissas de regressão logística

Regressão logística é uma técnica para prever uma
Variável de resultado dicotômica a partir de 1+ preditores.Exemplo: qual a probabilidade de as pessoas morrerem antes de 2020, dada a sua idade em 2015? Note que “morrer” é uma variável dicotômica porque tem apenas 2 resultados possíveis (sim ou não).
Esta análise também é conhecida como regressão logística binária ou simplesmente “regressão logística”. Uma técnica relacionada é a regressão logística multinomial que prediz variáveis de resultados com 3+ categorias.

Regressão logística – Exemplo simples

Um lar de idosos tem dados sobre N = 284 clientes do sexo, idade em 1 de Janeiro de 2015 e se o cliente faleceu antes de 1 de Janeiro de 2020. Os dados em bruto estão neste Googlesheet, parcialmente mostrados abaixo.

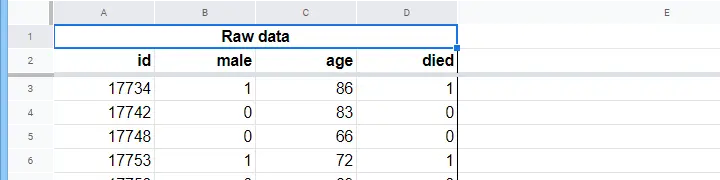
Vamos primeiro focar apenas na idade:podemos prever a morte antes de 2020 a partir da idade em 2015?e – se assim for – como? E até que ponto? Um bom primeiro passo é inspecionar um gráfico de dispersão como o mostrado abaixo.

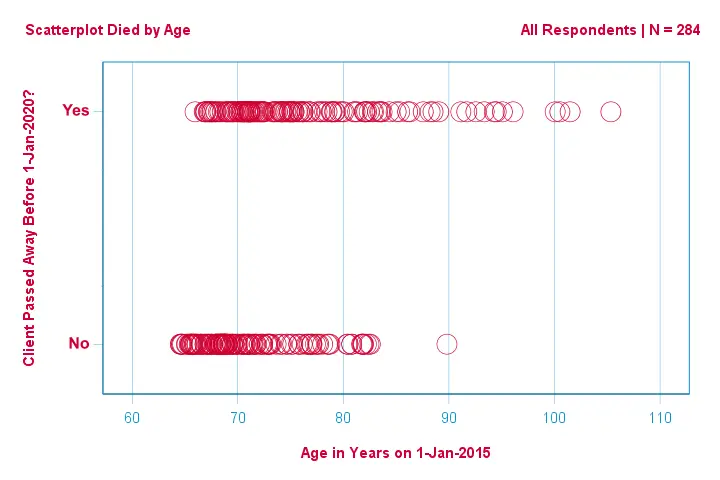
Poucas coisas que vemos neste gráfico de dispersão são que

• todos os clientes com mais de 83 anos de idade morreram nos 5 anos seguintes;
• o desvio padrão da idade é muito maior para os clientes que morreram do que para os clientes que sobreviveram;
• a idade tem uma considerável inclinação positiva, especialmente para os clientes que morreram.

Mas como podemos prever se um cliente morreu, dada a sua idade? Vamos fazer isso mesmo, encaixando uma curva logística.

Equação de regressão logística simples

Regressão logística simples calcula a probabilidade de algum resultado dado a uma única variável preditora como

$$P(Y_i) = \frac{1}{1 + e^{\},-,(b_0\,+\,b_1X_{1i}}$$

where

• (P(Y_i)}) é a probabilidade prevista de que a probabilidade prevista é verdadeira para o caso;
• (e) é uma constante matemática de aproximadamente 2.72;
• (b_0\) é uma constante estimada a partir dos dados;
• (b_1\) é uma constante estimada a partir dos dados;
• (X_i\) é a pontuação observada na variável \(X) para o caso \(i).

A própria essência da regressão logística é estimar { b_0} e { b_1}. Estes 2 números permitem-nos calcular a probabilidade de um cliente morrer, dada qualquer idade observada. Vamos ilustrar isto com alguns exemplos de curvas que adicionamos ao gráfico de dispersão anterior.

Curvas de Exemplo de Regressão Lógica

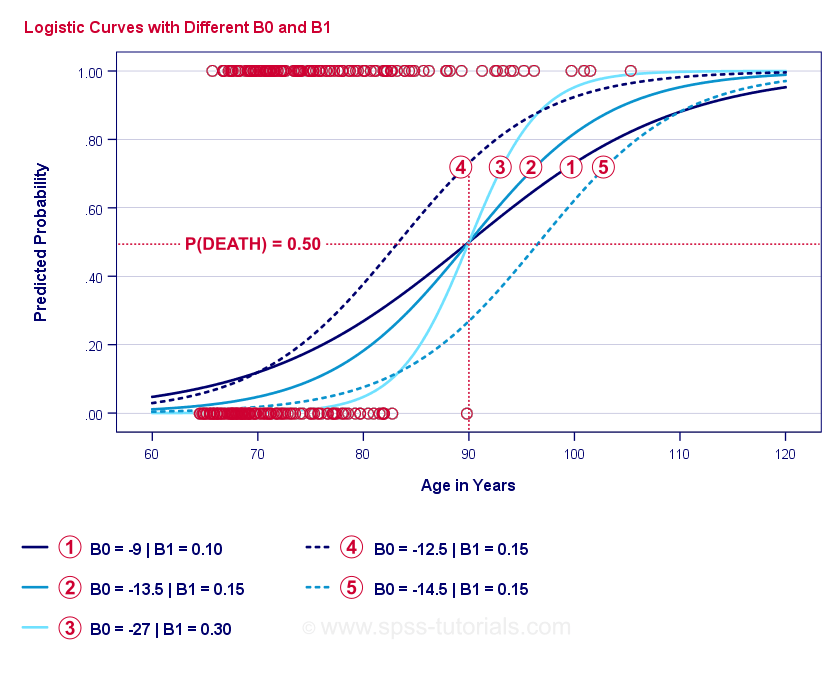
Se você levar um minuto para comparar estas curvas, você pode ver o seguinte:

• \(b_0\) determina a posição horizontal das curvas: conforme \(b_0\) aumenta, as curvas se deslocam para a esquerda, mas suas inclinações não são afetadas. Isto é visto para curvas , e . Note que { b_0} é diferente mas { b_1}é igual para estas curvas.

>

• Quando aumenta, as probabilidades previstas aumentam também: dada a idade = 90 anos, a curva prevê uma probabilidade aproximada de 0,75 de morrer. Curvas e prevêem cerca de 0,50 e 0,25 probabilidades de morrer para um cliente de 90 anos.
• \\(b_1\) determina a inclinação das curvas: se \(b_1\) > 0, a probabilidade de morrer também aumenta com o aumento da idade. Esta relação torna-se mais forte à medida que o { b_1}(b_1}) se torna maior. Curvas , e ilustram este ponto: à medida que \(b_1\) se torna maior, as curvas tornam-se mais íngremes para que a probabilidade de morrer aumente mais rapidamente com o aumento da idade.

Por enquanto, resta-nos uma pergunta: como encontrar o “melhor” \(b_0\) e \(b_1\)?

Regressão Logística – Probabilidade Logística

Para cada respondente, um modelo de regressão logística estima a probabilidade de ocorrência de algum evento \(Y_i\). Obviamente, estas probabilidades devem ser altas se o evento realmente ocorreu e reverter. Uma maneira de resumir o desempenho de algum modelo para todos os respondentes é a probabilidade de log-likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

where

• \(Y_i\) é 1 se o evento ocorreu e 0 se não ocorreu;
• (ln) denota o logaritmo natural: a que potência você deve elevar \(e) para obter um determinado número?

(LL) é uma medida de adequação: tudo o resto é igual, um modelo de regressão logística encaixa melhor nos dados na medida em que { LL} é maior. De forma um pouco confusa, é sempre negativo. Portanto, queremos encontrar a estimativa de probabilidade máxima (b_0) e a estimativa de probabilidade mínima (b_1) para as quais a regressão logística não pode calcular facilmente os valores ótimos para a regressão linear (b_0) e a regressão logística (b_1). Em vez disso, precisamos tentar números diferentes até que \i(LL) não aumente mais. Cada uma dessas tentativas é conhecida como uma iteração. O processo de encontrar valores ótimos através dessas iterações é conhecido como estimativa de máxima verosimilhança.

Então é basicamente assim que softwares estatísticos -como SPSS, Stata ou SAS- obtêm resultados de regressão logística. Felizmente, eles são incrivelmente bons nisso. Mas ao invés de relatar, estes pacotes relatam -2LL (-2LL).{\i1}(-2LL}) é uma medida “badness-of-fit” que segue uma
chi-square-distribution.{\i} Isto faz com que seja útil para comparar diferentes modelos, como veremos em breve. \A nota de rodapé aqui diz-nos que a estimativa da máxima verosimilhança necessitou apenas de 5 iterações para encontrar os coeficientes b óptimos. Então vamos olhar para essas agora.

Regressão logística – Coeficientes B

Os resultados mais importantes para qualquer análise de regressão logística são os coeficientes b. A figura abaixo mostra-os para os nossos dados de exemplo.

Antes de entrar em detalhes, esta saída mostra brevemente

os b-coeficientes que compõem nosso modelo;
os erros padrão para estes b-coeficientes;
a estatística de Wald -computada como \((\frac{B}{SE})^2\)- que segue uma distribuição qui-quadrada;
os graus de liberdade para a estatística de Wald;
os níveis de significância para os b-coeficientes;
os b-coeficientes exponenciados ou \(e^B\) são os odds ratios associados a mudanças nos escores preditores;
o intervalo de confiança de 95% para os b-coeficientes exponenciados.

Os b-coeficientes completam nosso modelo de regressão logística, que agora é

$$P(death_i) = \frac{1}{1 + e^{\,-,-,(-9.079,+\,0.124\, \cdot, age_i)}$$$

Para um cliente de 75 anos, a probabilidade de falecer dentro de 5 anos é

$$P(death_i) = \frac{1}{1 + e^{\,-,-,(-9.079\,+\,0.124\, {\cdot\, 75)}}=$$$

$$$P(death_i) = \frac{1}{1 + e^{\,-\,0.249}}=$$

$$P(death_i) = \frac{1}{1 + 0.780}=$$$

$$P(death_i) \aproximadamente 0,562$$

Então agora sabemos como prever a morte dentro de 5 anos, dada a idade de alguém. Mas quão boa é esta predição? Há várias abordagens. Vamos começar com comparações de modelos.

Regressão Lógica – Modelo Baseline

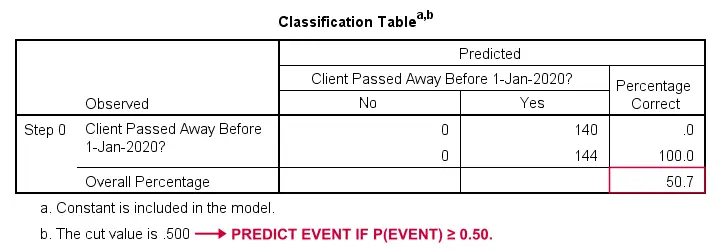
Como poderíamos prever quem faleceu se não tivéssemos nenhuma outra informação? Bem, 50,7% da nossa amostra faleceu. Então a probabilidade prevista seria simplesmente 0,507 para todos.

Para fins de classificação, normalmente prevemos que um evento ocorra se p(event) ≥ 0,50. Como p(died) = 0.507 para todos, nós simplesmente prevemos que todos faleceram. Esta previsão é correta para os 50,7% da nossa amostra que morreram.

Regressão Lógica – Razão de Probabilidade

Agora, a partir dessas probabilidades previstas e dos resultados observados podemos calcular nossa medida de badness-of-fit: -2LLL = 393,65. Nosso modelo atual -previsão de morte por idade- vem com -2LL = 354,20. A diferença entre estes números é conhecida como a razão de verosimilhança (LR):

$$LR = (-2LLL_{base}) – (-2LLL_{modelo})$$

Importantemente, { LR} segue uma distribuição qui-quadrada com graus de liberdade, calculado como

$$df = k_{model} – k_{baseline}$$

onde \(k\) denota o número de parâmetros estimados pelos modelos. Como mostrado nesta folha do Googlesheet, \(LR) e \(df) resultam em um nível de significância para todo o modelo.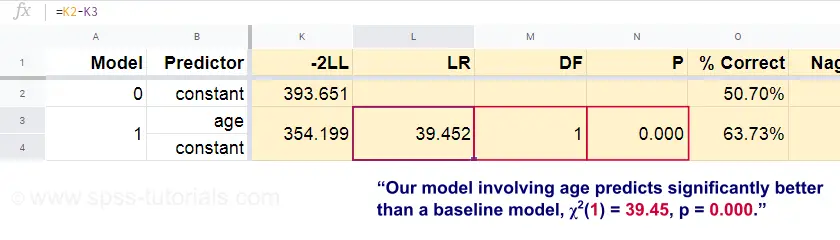

A hipótese nula aqui é que algum modelo prevê igualmente mal como o modelo de base em alguma população. Como p = 0.000, nós rejeitamos isto: nosso modelo (prevendo a morte a partir da idade) tem um desempenho significativamente melhor do que um modelo de linha de base sem nenhum preditor.
Mas precisamente quanto melhor? Isto é respondido pelo seu tamanho de efeito.

Regressão Lógica – Tamanho do Efeito do Modelo

Uma boa maneira de avaliar o desempenho do nosso modelo é a partir de uma medida de tamanho de efeito. Uma opção é o Cox & Snell R2 ou \(R^2_{CS}}} calculado como

$$$R^2_{CS} = 1 – e^{\frac{(-2LLL_{model})\,-\,(-2LLL_{baseline})}{n}}$$

Sadly, \(R^2_{CS}) nunca atinge o seu máximo teórico de 1. Portanto, uma versão ajustada conhecida como Nagelkerke R2 ou \(R^2_{N}}} é frequentemente preferida:

$$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LLL_{base}}{n}}}$$$

Para os nossos dados de exemplo, \(R^2_{CS}} = 0,130 o que indica um tamanho de efeito médio. \(R^2_{N}} = 0,173, ligeiramente maior que o tamanho médio.

Last, \(R^2_{CS}}) e \(R^2_{N}) são tecnicamente completamente diferentes do quadrado r como computado em regressão linear. No entanto, eles tentam cumprir o mesmo papel. Portanto, ambas as medidas são conhecidas como medidas pseudo r-quadradas.

Regressão Lógica – Tamanho do Efeito Preditor

Estranhamente, muito poucos livros de texto mencionam qualquer tamanho de efeito para preditores individuais. Talvez isso seja porque estes estão completamente ausentes do SPSS. A razão porque precisamos deles é que os b-coeffients dependem das escalas (arbitrárias) dos nossos preditores:se nós entrássemos na idade em dias ao invés de anos, seu b-coeffient encolheria tremendamente. Isto obviamente torna os b-coeficientes inadequados para comparar preditores dentro ou entre diferentes modelos.
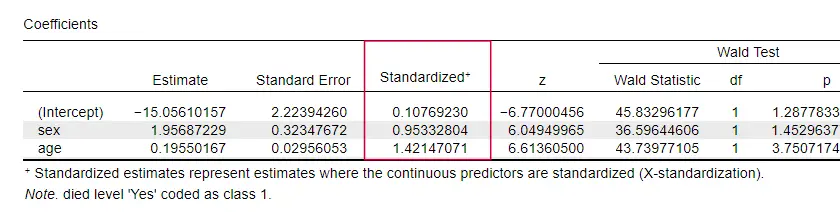
JASP inclui b-coeficientes parcialmente padronizados: os preditores quantitativos – mas não a variável de resultado – são inseridos como z-scores, como mostrado abaixo.

Premissas de regressão logística

Análise de regressão logística requer as seguintes premissas:

1. observações independentes;
2. especificação correta do modelo;
3. medida sem erros da variável de resultado e de todos os preditores;
4. linearidade: cada preditor está relacionado linearmente com \(e^B\) (o odds ratio).

A suposição 4 é algo discutível e omitida por muitos livros1,6. Ela pode ser avaliada com o teste Box-Tidwell, conforme discutido pelo Field4. Isto se resume basicamente a testar se há algum efeito de interação entre cada preditor e seu logaritmo natural ou \(LN\).

Regressão logística múltipla

A nossa discussão limitou-se à regressão logística simples que usa apenas um preditor. O modelo é facilmente estendido com preditores adicionais, resultando em regressão logística múltipla:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0,+\,b_1X_{1i}+\,b_2X_{2i}+\,…+\,b_kX_{ki}}$$

onde

• \\(P(Y_i)}) é a probabilidade prevista de que {\i}(Y)} seja verdade para o caso {\i};
• (e) é uma constante matemática de aproximadamente 2.72;
• (b_0\) é uma constante estimada a partir dos dados;
• (b_1\), { b_2\), … são os b-coeficientes para os preditores 1, 2, … …88898
• (X_{1i}), X_2i), … … são observadas pontuações em preditores,… …,X_k) para o caso

Regressão logística múltipla envolve frequentemente a selecção do modelo e a verificação da multicolinearidade. Fora isso, é uma extensão bastante simples da regressão logística simples.

Esta introdução básica foi limitada ao essencial da regressão logística. Se você gostaria de aprender mais, você pode querer ler sobre alguns dos tópicos que omitimos:

1. os rácios de probabilidade -computados como \(e^B\) na regressão logística- expressam como as probabilidades mudam dependendo dos resultados dos preditores ;
2. o teste Box-Tidwell examina se as relações entre os rácios de probabilidade acima mencionados e os resultados dos preditores são lineares;
3. o teste Hosmer e Lemeshow é um teste alternativo de goodness-of-fit para todo um modelo de regressão logística.

>

Prazos de leitura!

1. Warner, R.M. (2013). Estatística Aplicada (2ª Edição). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Estatística. A Arte & Science of Learning from Data (Ciência da Aprendizagem de Dados). Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Análise Multivariada de Dados. Nova Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Descobrindo Estatísticas com as Estatísticas SPSS da IBM. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Métodos Estatísticos para Psicologia (5ª ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Estatística Multivariada Aplicada às Ciências Sociais (6ª ed.). Nova Iorque: Routledge.