• Ecuația de regresie logistică
• Curbe de exemplu de regresie logistică
• Regresia logistică – Coeficienți B
• Regresie logistică – Mărimea efectului
• Ipotezele regresiei logistice

Regresia logistică este o tehnică de predicție a unei variabile de rezultat
dichotomice din 1+ predictori.Exemplu: Care este probabilitatea ca oamenii să moară înainte de 2020, având în vedere vârsta lor în 2015? Rețineți că „a muri” este o variabilă dihotomică, deoarece are doar 2 rezultate posibile (da sau nu).
Această analiză este cunoscută și sub numele de regresie logistică binară sau pur și simplu „regresie logistică”. O tehnică înrudită este regresia logistică multinomială, care prezice variabile de rezultat cu 3+ categorii.

Regresie logistică – Exemplu simplu

Un azil de bătrâni are date privind sexul N = 284 de clienți, vârsta la 1 ianuarie 2015 și dacă clientul a decedat înainte de 1 ianuarie 2020. Datele brute sunt în acest Googlesheet, parțial prezentate mai jos.

Să ne concentrăm mai întâi doar pe vârstă:putem prezice decesul înainte de 2020 pornind de la vârsta din 2015?Și -dacă da- cum anume? Și în ce măsură? Un prim pas bun este inspectarea unei diagrame de dispersie precum cea prezentată mai jos.

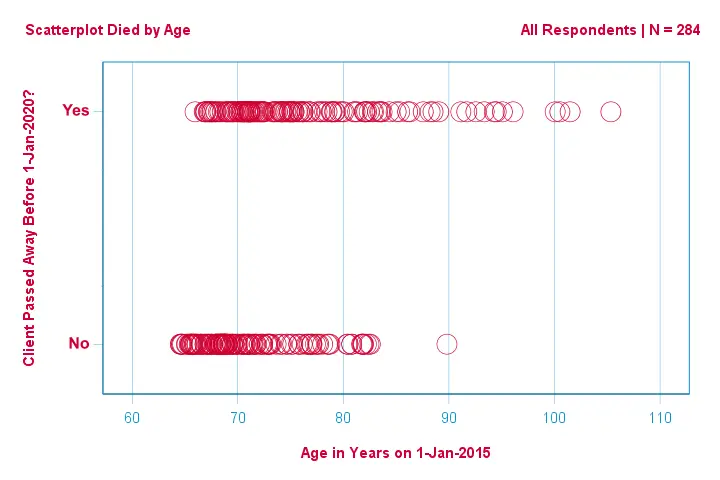
Câteva lucruri pe care le vedem în această diagramă de dispersie sunt că

• toți clienții cu vârsta de peste 83 de ani, cu excepția unuia, au murit în următorii 5 ani;
• deviația standard a vârstei este mult mai mare pentru clienții care au murit decât pentru clienții care au supraviețuit;
• vechimea are o asimetrie pozitivă considerabilă, în special pentru clienții care au murit.

Dar cum putem prezice dacă un client a murit, având în vedere vârsta sa? Vom face exact acest lucru prin ajustarea unei curbe logistice.

Ecuația de regresie logistică simplă

Regresia logistică simplă calculează probabilitatea unui anumit rezultat având în vedere o singură variabilă predictoare ca

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}$$

unde

• \(P(Y_i)\) este probabilitatea prezisă ca \(Y\) să fie adevărată pentru cazul \(i\);
• \(e\) este o constantă matematică de aproximativ 2.72;
• \(b_0\) este o constantă estimată din date;
• \(b_1\) este un coeficient b estimat din date;
• \(X_i\) este scorul observat pe variabila \(X\) pentru cazul \(i\).

Esența însăși a regresiei logistice este estimarea \(b_0\) și \(b_1\). Aceste 2 numere ne permit să calculăm probabilitatea ca un client să moară având în vedere orice vârstă observată. Vom ilustra acest lucru cu câteva exemple de curbe pe care le-am adăugat la diagrama de dispersie anterioară.

Curbe de exemplu de regresie logistică

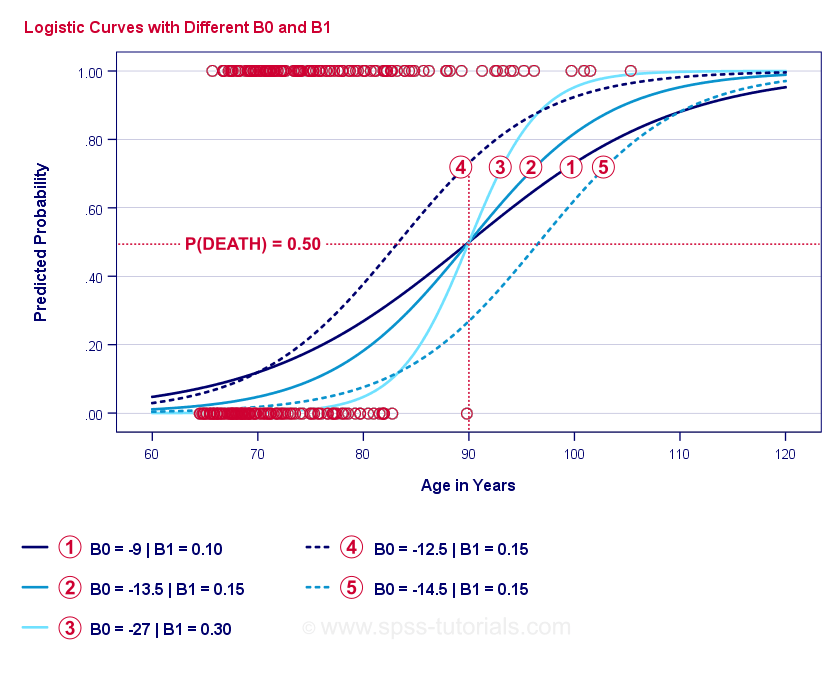
Dacă vă luați un minut pentru a compara aceste curbe, puteți observa următoarele:

• \(b_0\) determină poziția orizontală a curbelor: pe măsură ce \(b_0\) crește, curbele se deplasează spre stânga, dar abrupturile lor nu sunt afectate. Acest lucru se observă în cazul curbelor , și . Observați că \(b_0\) este diferit, dar \(b_1\) este egal pentru aceste curbe.
• Pe măsură ce \(b_0\) crește, cresc și probabilitățile prezise: dată fiind vârsta = 90 de ani, curba prezice o probabilitate de aproximativ 0,75 de a muri. Curbele și prezic aproximativ 0,50 și 0,25 probabilități de a muri pentru un client în vârstă de 90 de ani.
• \(b_1\) determină abruptul curbelor: dacă \(b_1\) > 0, probabilitatea de a muri crește odată cu înaintarea în vârstă. Această relație devine mai puternică pe măsură ce \(b_1\) devine mai mare. Curbele , și ilustrează acest aspect: pe măsură ce \(b_1\) devine mai mare, curbele devin mai abrupte, astfel încât probabilitatea de a muri crește mai repede odată cu înaintarea în vârstă.

Pentru moment, ne-a mai rămas o întrebare: cum găsim cele mai „bune” \(b_0\) și \(b_1\)?

Regresie logistică – Log probabilitate

Pentru fiecare respondent, un model de regresie logistică estimează probabilitatea ca un anumit eveniment \(Y_i\) să se fi produs. Evident, aceste probabilități ar trebui să fie ridicate dacă evenimentul s-a produs efectiv și invers. Un mod de a rezuma cât de bine se comportă un anumit model pentru toți respondenții este probabilitatea logaritmică \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

unde

• \(Y_i\) este 1 dacă evenimentul a avut loc și 0 dacă nu a avut loc;
• \(ln\) denumește logaritmul natural: la ce putere trebuie să ridicați \(e\) pentru a obține un număr dat?

\(LL\) este o măsură a bonității de potrivire: în rest, în condiții de egalitate, un model de regresie logistică se potrivește mai bine datelor în măsura în care \(LL\) este mai mare. În mod oarecum confuz, \(LL\) este întotdeauna negativ. Așadar, dorim să găsim \(b_0\) și \(b_1\) pentru care
\(LL\) este cât mai aproape de zero.

Stimare de maximă verosimilitate

În contrast cu regresia liniară, regresia logistică nu poate calcula cu ușurință valorile optime pentru \(b_0\) și \(b_1\). În schimb, trebuie să încercăm diferite numere până când \(LL\) nu mai crește. Fiecare astfel de încercare este cunoscută ca o iterație. Procesul de găsire a valorilor optime prin astfel de iterații este cunoscut sub numele de estimare de maximă verosimilitate.

Atunci, practic, acesta este modul în care programele statistice – cum ar fi SPSS, Stata sau SAS – obțin rezultatele regresiei logistice. Din fericire, ele sunt uimitor de bune la asta. Dar, în loc să raporteze \(LL\), aceste pachete raportează \(-2LL\).\(-2LL\) este o măsură de „badness-of-fit” care urmează o distribuție
chi-pătrată.Acest lucru face ca \(-2LL\) să fie utilă pentru a compara diferite modele, așa cum vom vedea în scurt timp. \(-2LL\) este notat ca -2 Log likelihood în rezultatul prezentat mai jos.

Nota de subsol de aici ne spune că estimarea de maximă verosimilitate a avut nevoie de numai 5 iterații pentru a găsi coeficienții b optimi \(b_0\) și \(b_1\). Așa că haideți să ne uităm la aceștia acum.

Regresie logistică – Coeficienți B

Cel mai important rezultat pentru orice analiză de regresie logistică sunt coeficienții b. Figura de mai jos îi prezintă pentru datele din exemplul nostru.

Înainte de a intra în detalii, această ieșire arată pe scurt

coeficienții b care alcătuiesc modelul nostru;
erorile standard pentru acești coeficienți b;
statistica Wald -calculată ca \((\frac{B}{SE})^2\)- care urmează o distribuție chi-pătrat;
gradele de libertate pentru statistica Wald;
nivelurile de semnificație pentru coeficienții b;
coeficienții b exponențiali sau \(e^B\) sunt cotele de probabilitate asociate cu modificările scorurilor predictorilor;
intervalul de încredere de 95% pentru coeficienții b exponențiali.

Coeficienții b completează modelul nostru de regresie logistică, care este acum

$$$P(deces_i) = \frac{1}{1 + e^{\,-\,(-9,079\,+\,0.124\, \cdot\, age_i)}}$$$

Pentru un client în vârstă de 75 de ani, probabilitatea de a deceda în 5 ani este

$$P(deces_i) = \frac{1}{1 + e^{\,-\,(-9.079\\,+\,0.124\, \cdot\, 75)}}=$$

$$P(deces_i) = \frac{1}{1 + e^{\,-\,-\,0.249}}=$$

$$P(deces_i) = \frac{1}{1 + 0.780}=$$

$$P(deces_i) \aproximativ 0,562$$

Acum știm cum să prezicem decesul în 5 ani, dată fiind vârsta cuiva. Dar cât de bună este această predicție? Există mai multe abordări. Să începem cu compararea modelelor.

Regresie logistică – Model de bază

Cum am putea prezice cine a decedat dacă nu am avea alte informații? Ei bine, 50,7% din eșantionul nostru a decedat. Deci probabilitatea prezisă ar fi pur și simplu 0,507 pentru toată lumea.

În scopul clasificării, de obicei prezicem că un eveniment are loc dacă p(eveniment) ≥ 0,50. Deoarece p(a murit) = 0,507 pentru toată lumea, prezicem pur și simplu că toată lumea a decedat. Această predicție este corectă pentru cei 50,7% din eșantionul nostru care au murit.

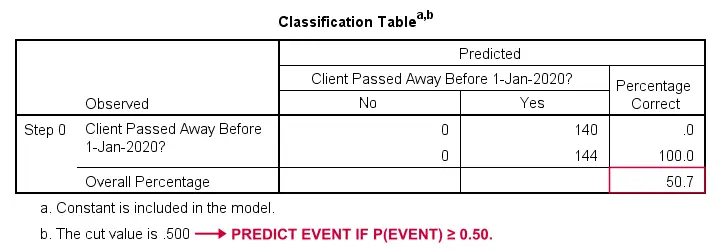
Regresie logistică – Raportul de verosimilitate

Acum, pornind de la aceste probabilități prezise și de la rezultatele observate, putem calcula măsura noastră de inadecvare: -2LL = 393,65. Modelul nostru real -predicând decesul din cauza vârstei- iese cu -2LL = 354,20. Diferența dintre aceste numere este cunoscută sub numele de raportul de verosimilitate \(LR\):

$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Important, \(LR\) urmează o distribuție chi-pătrat cu \(df\) grade de libertate, calculată ca

$$df = k_{model} – k_{baseline}$$$

unde \(k\) reprezintă numărul de parametri estimați de modele. După cum se arată în această foaie de Googlesheet, \(LR\) și \(df\) au ca rezultat un nivel de semnificație pentru întregul model.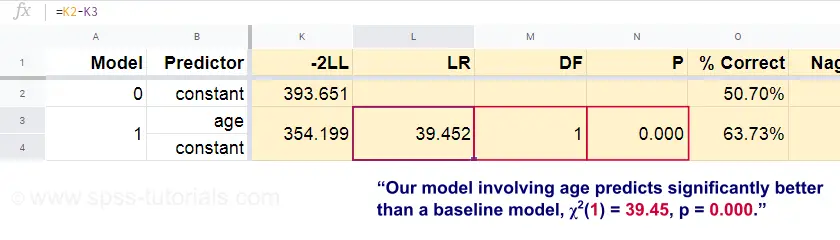

Ipoteza nulă aici este că un anumit model prezice la fel de slab ca și modelul de bază în anumite populații. Din moment ce p = 0,000, respingem această ipoteză: modelul nostru (care prezice decesul din cauza vârstei) performează semnificativ mai bine decât un model de bază fără niciun predictor.
Dar cu cât de mult mai bine, mai exact? Răspunsul la această întrebare este dat de mărimea efectului său.

Regresie logistică – Mărimea efectului modelului

O modalitate bună de a evalua cât de bine se comportă modelul nostru este prin prisma unei măsuri a mărimii efectului. O opțiune este Cox & Snell R2 sau \(R^2_{CS}\) calculat ca

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-\,(-2LL_{baseline})}{n}}$$$

Din păcate, \(R^2_{CS}\) nu atinge niciodată maximul său teoretic de 1. Prin urmare, o versiune ajustată cunoscută sub numele de Nagelkerke R2 sau \(R^2_{N}\) este adesea preferată:

$$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}}$$

Pentru datele din exemplul nostru, \(R^2_{CS}\) = 0,130, ceea ce indică o dimensiune medie a efectului. \(R^2_{N}\) = 0,173, ușor mai mare decât mediu.

În sfârșit, \(R^2_{CS}\) și \(R^2_{N}\ sunt, din punct de vedere tehnic, complet diferite de r-pătrat calculat în regresia liniară. Cu toate acestea, ele încearcă să îndeplinească același rol. Ambele măsuri sunt, prin urmare, cunoscute ca măsuri de pseudo r pătrat.

Regresie logistică – Mărimea efectului predictorului

În mod ciudat, foarte puține manuale menționează vreo mărime a efectului pentru predictorii individuali. Poate că acest lucru se datorează faptului că acestea sunt complet absente din SPSS. Motivul pentru care avem nevoie de ele este acela că b-coeficienții depind de scările (arbitrare) ale predictorilor noștri:dacă am introduce vârsta în zile în loc de ani, b-coeficiența sa s-ar micșora foarte mult. În mod evident, acest lucru face ca b-coeficienții să fie nepotriviți pentru a compara predictorii în cadrul sau între diferite modele.
JASP include b-coeficienți parțial standardizați: predictorii cantitativi -dar nu și variabila de rezultat- sunt introduși ca scoruri z, așa cum se arată mai jos.

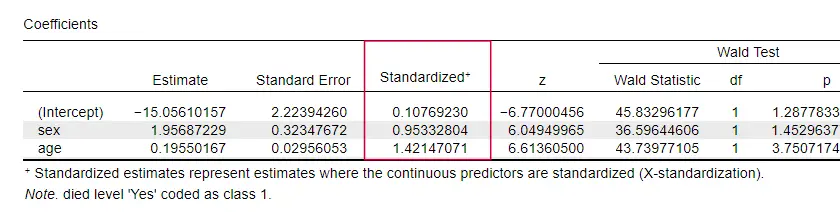
Ipoteze de regresie logistică

Analiza de regresie logistică necesită următoarele ipoteze:

1. observații independente;
2. specificarea corectă a modelului;
3. măsurarea fără erori a variabilei de rezultat și a tuturor predictorilor;
4. linearitate: fiecare predictor este legat liniar de \(e^B\) (raportul cotelor).

Asumpția 4 este oarecum discutabilă și este omisă de multe manuale1,6. Ea poate fi evaluată cu ajutorul testului Box-Tidwell, așa cum a fost discutat de Field4. Practic, aceasta se reduce la a testa dacă există efecte de interacțiune între fiecare predictor și logaritmul său natural sau \(LN\).

Regresie logistică multiplă

Până acum, discuția noastră s-a limitat la regresia logistică simplă, care utilizează un singur predictor. Modelul este ușor de extins cu predictori suplimentari, rezultând o regresie logistică multiplă:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,…+\,b_kX_{ki})}}$$

unde

• \(P(Y_i)\) este probabilitatea prezisă că \(Y\) este adevărată pentru cazul \(i\);
• \(e\) este o constantă matematică de aproximativ 2.72;
• \(b_0\) este o constantă estimată din date;
• \(b_1\), \(b_2\), … ,\(b_k\) sunt coeficienții b pentru predictorii 1, 2, …. ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) sunt scorurile observate pe predictorii \(X_1\), \(X_2\), … ,\(X_k\) pentru cazul \(i\).

Regresia logistică multiplă implică adesea selectarea modelului și verificarea multicolinearității. În afară de aceasta, este o extensie destul de simplă a regresiei logistice simple.

Acestă introducere de bază s-a limitat la elementele esențiale ale regresiei logistice. Dacă doriți să aflați mai multe, este posibil să doriți să citiți despre unele dintre subiectele pe care le-am omis:

1. raporturile de cote -calculate ca \(e^B\) în regresia logistică- exprimă modul în care se modifică probabilitățile în funcție de scorurile predictorilor ;
2. testul Box-Tidwell examinează dacă relațiile dintre cotele de cote menționate anterior și scorurile predictorilor sunt liniare;
3. testul Hosmer și Lemeshow este un test alternativ de bonitate a adecvării pentru un întreg model de regresie logistică.

Mulțumim pentru lectură!

1. Warner, R.M. (2013). Statistică aplicată (Ediția a 2-a.). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistică. The Art & Science of Learning from Data (Arta & Știința de a învăța din date). Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al. (2006). Analiza datelor multivariate. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Descoperirea statisticii cu IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Metode statistice pentru psihologie (5th ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Statistică multivariată aplicată pentru științele sociale (ediția a 6-a.). New York: Routledge.

.