Introducción

El árbol de decisión es un tipo de algoritmo de aprendizaje supervisado que puede utilizarse tanto en problemas de regresión como de clasificación. Funciona tanto para variables de entrada como de salida categóricas y continuas.

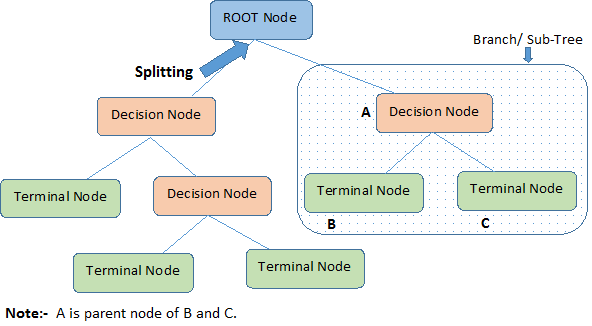
Identificamos terminologías importantes sobre el Árbol de Decisión, mirando la imagen de arriba:

• El Nodo Raíz representa toda la población o muestra. Además, se divide en dos o más conjuntos homogéneos.

• La división es un proceso que consiste en dividir un nodo en dos o más subnodos.

• Cuando un subnodo se divide en otros subnodos, se denomina nodo de decisión.

• Los nodos que no se dividen se llaman Nodo Terminal u Hoja.

• Cuando se eliminan los subnodos de un nodo de decisión, este proceso se llama Poda. Lo contrario de la poda es el Splitting.

• Una sub-sección de un árbol entero se llama Branch.

• Un nodo, que se divide en sub-nodos se llama nodo padre de los sub-nodos; mientras que los sub-nodos se llaman hijo del nodo padre.

Tipos de Árboles de Decisión

Árboles de Regresión

Veamos la siguiente imagen, que ayuda a visualizar la naturaleza de la partición realizada por un Árbol de Regresión. Muestra un árbol no podado y un árbol de regresión ajustado a un conjunto de datos aleatorio. Ambas visualizaciones muestran una serie de reglas de división, empezando por la parte superior del árbol. Observe que cada división del dominio está alineada con uno de los ejes de características. El concepto de división paralela a los ejes se generaliza directamente a dimensiones superiores a dos. Para un espacio de características de tamaño $p$, un subconjunto de $\mathbb{R}^p$, el espacio se divide en $M$ regiones, $R_{m}$, cada una de las cuales es un «hiperbloque» $p$-dimensional.

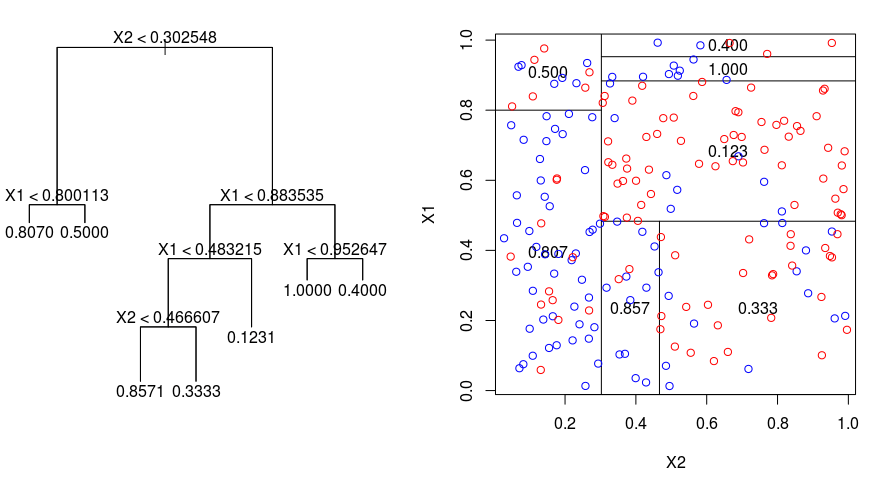
Para construir un árbol de regresión, primero se utiliza la división binaria recursiva para hacer crecer un gran árbol en los datos de entrenamiento, deteniéndose sólo cuando cada nodo terminal tiene menos de un número mínimo de observaciones. La división binaria recursiva es un algoritmo codicioso y descendente que se utiliza para minimizar la suma residual de cuadrados (RSS), una medida de error que también se utiliza en los entornos de regresión lineal. El RSS, en el caso de un espacio de características con M particiones, viene dado por:

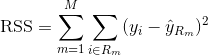
Comenzando por la parte superior del árbol, se divide en 2 ramas, creando una partición de 2 espacios. A continuación, se lleva a cabo esta partición particular en la parte superior del árbol varias veces y se elige la partición de las características que minimiza el RSS (actual).

A continuación, se aplica la poda de complejidad de costes al árbol grande para obtener una secuencia de mejores subárboles, en función de $\alpha$. La idea básica aquí es introducir un parámetro de ajuste adicional, denotado por $\alpha$ que equilibra la profundidad del árbol y su bondad de ajuste a los datos de entrenamiento.

Puede utilizar la validación cruzada K-fold para elegir $\alpha$. Esta técnica consiste simplemente en dividir las observaciones de entrenamiento en K pliegues para estimar la tasa de error de prueba de los subárboles. Su objetivo es seleccionar el que conduce a la tasa de error más baja.

Árboles de clasificación

Un árbol de clasificación es muy similar a un árbol de regresión, excepto que se utiliza para predecir una respuesta cualitativa en lugar de una cuantitativa.

Recuerde que para un árbol de regresión, la respuesta predicha para una observación está dada por la respuesta media de las observaciones de entrenamiento que pertenecen al mismo nodo terminal. Por el contrario, para un árbol de clasificación, se predice que cada observación pertenece a la clase más común de las observaciones de entrenamiento en la región a la que pertenece.

Al interpretar los resultados de un árbol de clasificación, a menudo está interesado no sólo en la predicción de la clase correspondiente a una región de nodo terminal en particular, sino también en las proporciones de clase entre las observaciones de entrenamiento que caen en esa región.

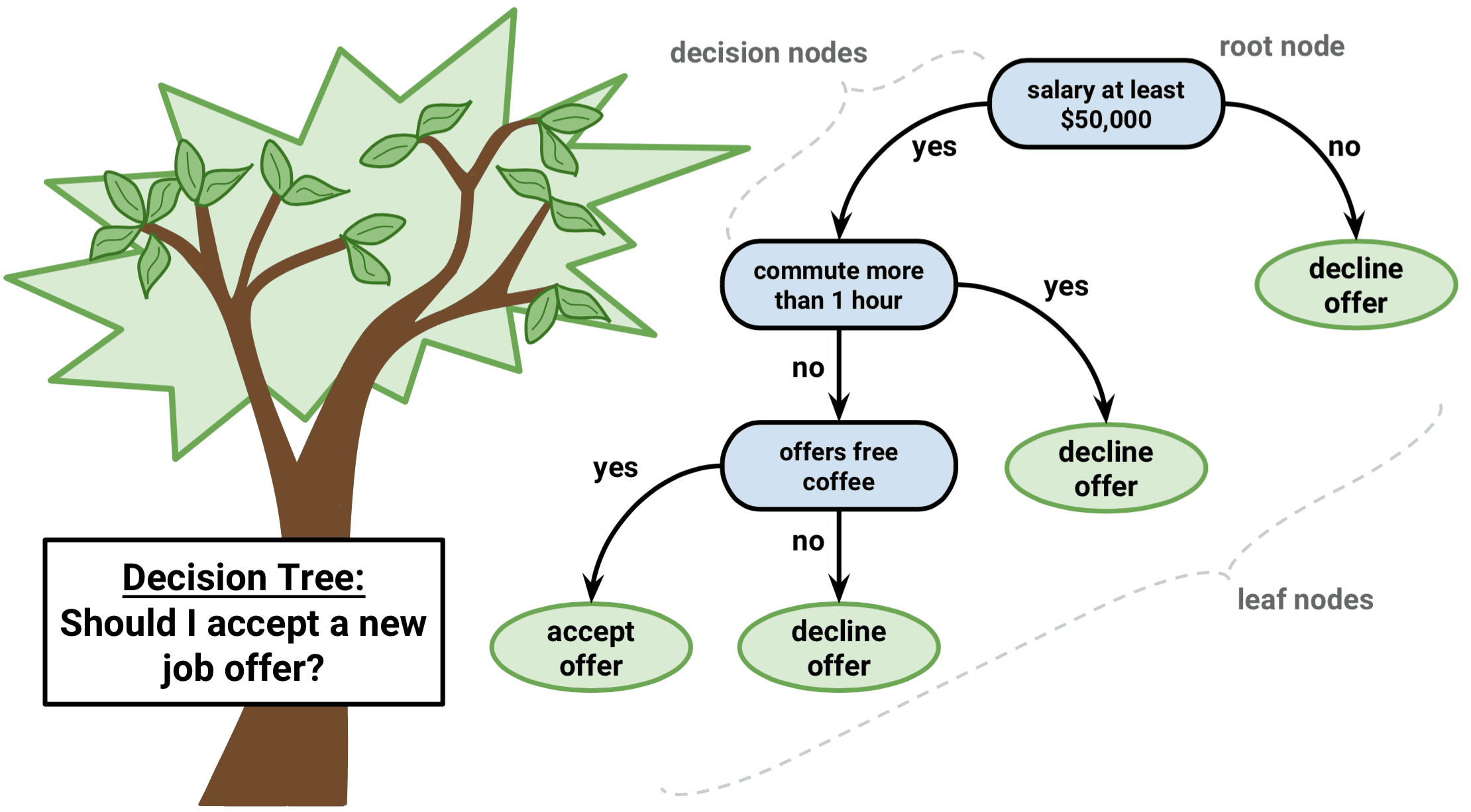
La tarea de hacer crecer un árbol de clasificación es bastante similar a la tarea de hacer crecer un árbol de regresión. Al igual que en la configuración de regresión, se utiliza la división binaria recursiva para hacer crecer un árbol de clasificación. Sin embargo, en la configuración de clasificación, la suma residual de cuadrados no se puede utilizar como criterio para realizar las divisiones binarias. En su lugar, puede utilizar cualquiera de estos 3 métodos siguientes:

• Tasa de error de clasificación: En lugar de ver lo lejos que está una respuesta numérica del valor medio, como en la configuración de la regresión, puede definir la «tasa de aciertos» como la fracción de observaciones de entrenamiento en una región particular que no pertenecen a la clase de mayor ocurrencia. El error viene dado por esta ecuación:

E = 1 – argmaxc($\hat{{pi}_{mc}$)

en la que $\hat{pi}_{mc}$ representa la fracción de datos de entrenamiento en la región Rm que pertenecen a la clase c.

• Índice de Gini: El índice de Gini es una métrica de error alternativa que está diseñada para mostrar cuán «pura» es una región. La «pureza» en este caso significa la cantidad de datos de entrenamiento en una región particular que pertenece a una sola clase. Si una región Rm contiene datos que pertenecen mayoritariamente a una única clase c, el valor del Índice de Gini será pequeño:

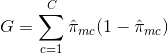
• Entropía cruzada: Una tercera alternativa, que es similar al índice de Gini, se conoce como entropía cruzada o desviación:

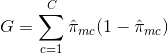
La entropía cruzada tomará un valor cercano a cero si los ${hat{pi}_{mc}$ están todos cerca de 0 o cerca de 1. Por lo tanto, al igual que el índice de Gini, la entropía cruzada tomará un valor pequeño si el m-ésimo nodo es puro. De hecho, resulta que el índice de Gini y la entropía cruzada son bastante similares numéricamente.

Cuando se construye un árbol de clasificación, se suele utilizar el índice de Gini o la entropía cruzada para evaluar la calidad de una determinada división, ya que son más sensibles a la pureza de los nodos que la tasa de error de clasificación. Cualquiera de estos 3 enfoques puede utilizarse al podar el árbol, pero la tasa de error de clasificación es preferible si el objetivo es la precisión de la predicción del árbol podado final.

Ventajas y desventajas de los árboles de decisión

La mayor ventaja de utilizar árboles de decisión es que son intuitivamente muy fáciles de explicar. Reflejan muy de cerca la toma de decisiones humana en comparación con otros enfoques de regresión y clasificación. Pueden visualizarse gráficamente y pueden manejar fácilmente predictores cualitativos sin necesidad de crear variables ficticias.

Sin embargo, los árboles de decisión generalmente no tienen el mismo nivel de precisión predictiva que otros enfoques, ya que no son del todo robustos. Un pequeño cambio en los datos puede provocar un gran cambio en el árbol final estimado.

Al agregar muchos árboles de decisión, utilizando métodos como bagging, bosques aleatorios y boosting, el rendimiento predictivo de los árboles de decisión puede mejorarse sustancialmente.

Métodos basados en árboles

Bagging

Los árboles de decisión discutidos anteriormente sufren de una alta varianza, lo que significa que si se dividen los datos de entrenamiento en 2 partes al azar, y se ajusta un árbol de decisión a ambas mitades, los resultados que se obtienen podrían ser muy diferentes. Por el contrario, un procedimiento con baja varianza producirá resultados similares si se aplica repetidamente a un conjunto de datos distinto.

El bagging, o agregación bootstrap, es una técnica utilizada para reducir la varianza de sus predicciones combinando el resultado de múltiples clasificadores modelados en diferentes submuestras del mismo conjunto de datos. Esta es la ecuación para el bagging:

en la que se generan $B$ diferentes conjuntos de datos de entrenamiento bootstrap. A continuación, entrena su método en el $bth$ conjunto de entrenamiento bootstrapped con el fin de obtener $\hat{f}_{b}(x)$, y, finalmente, el promedio de las predicciones.

El visual a continuación muestra los 3 pasos diferentes en el bagging:

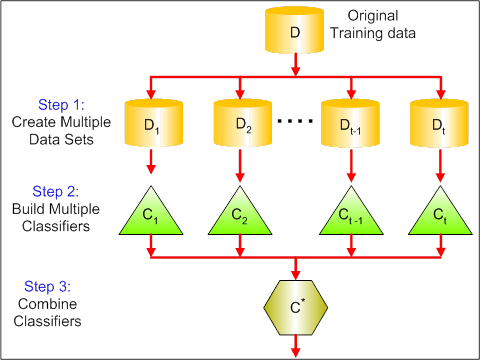
• Paso 1: Aquí reemplaza los datos originales con nuevos datos. Los nuevos datos suelen tener una fracción de las columnas y filas de los datos originales, que luego se pueden utilizar como hiperparámetros en el modelo de embolsamiento.

• Paso 2: Se construyen clasificadores en cada conjunto de datos. Generalmente, se puede utilizar el mismo clasificador para hacer modelos y predicciones.

• Paso 3: Por último, se utiliza un valor medio para combinar las predicciones de todos los clasificadores, dependiendo del problema. Generalmente, estos valores combinados son más robustos que un solo modelo.

Aunque el bagging puede mejorar las predicciones de muchos métodos de regresión y clasificación, es particularmente útil para los árboles de decisión. Para aplicar el ensacado a los árboles de regresión/clasificación, simplemente se construyen $B$ árboles de regresión/clasificación utilizando $B$ conjuntos de entrenamiento de arranque, y se promedian las predicciones resultantes. Estos árboles crecen en profundidad y no se podan. Por lo tanto, cada árbol individual tiene una alta varianza, pero un bajo sesgo. Al promediar estos $B$ árboles se reduce la varianza.

En términos generales, se ha demostrado que el ensacado proporciona impresionantes mejoras en la precisión al combinar cientos o incluso miles de árboles en un único procedimiento.

Bosques aleatorios

Los bosques aleatorios son un método de aprendizaje automático versátil capaz de realizar tanto tareas de regresión como de clasificación. También lleva a cabo métodos de reducción dimensional, trata los valores perdidos, los valores atípicos y otros pasos esenciales de la exploración de datos, y hace un trabajo bastante bueno.

Los Bosques Aleatorios proporcionan una mejora sobre los árboles embolsados mediante un pequeño ajuste que decorrelaciona los árboles. Al igual que en el embolsado, se construye un número de árboles de decisión en muestras de entrenamiento con un arranque. Pero cuando se construyen estos árboles de decisión, cada vez que se considera una división en un árbol, se elige una muestra aleatoria de m predictores como candidatos a la división del conjunto completo de $p$ predictores. La división sólo puede utilizar uno de esos $m$ predictores. Esta es la principal diferencia entre los bosques aleatorios y el bagging; porque al igual que en el bagging, la elección del predictor $m = p$.

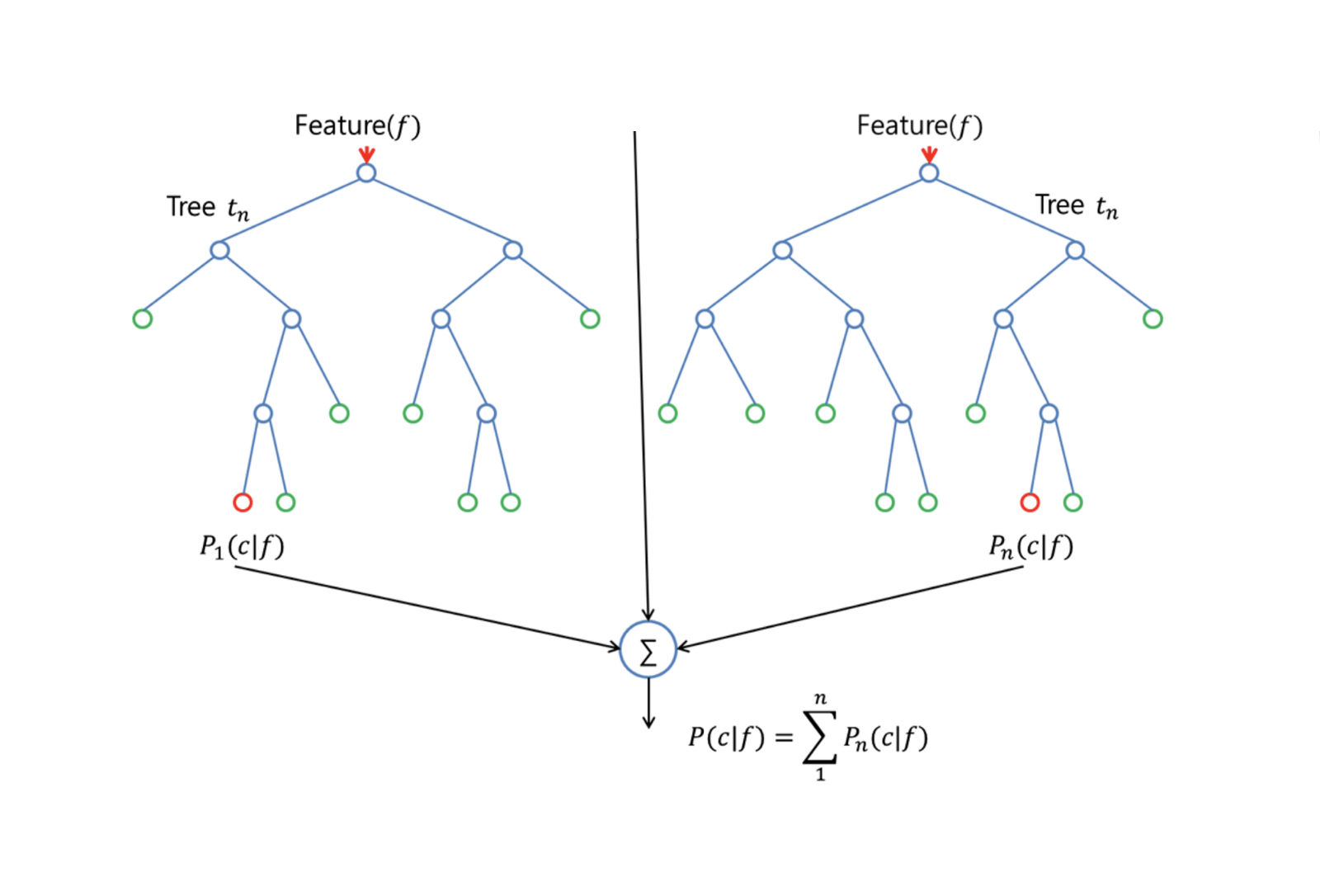
Para hacer crecer un bosque aleatorio, debería:

• Primero suponga que el número de casos en el conjunto de entrenamiento es K. A continuación, tomar una muestra aleatoria de estos K casos, y luego utilizar esta muestra como el conjunto de entrenamiento para el crecimiento del árbol.

• Si hay $p$ variables de entrada, especificar un número $m < p$ tal que en cada nodo, puede seleccionar $m$ variables aleatorias de los $p$. La mejor división de estas $m$ se utiliza para dividir el nodo.

• Cada árbol crece posteriormente hasta la mayor extensión posible y no es necesario realizar ninguna poda.

• Por último, agrega las predicciones de los árboles objetivo para predecir nuevos datos.

Los bosques aleatorios son muy eficaces para estimar los datos que faltan y mantener la precisión cuando falta una gran proporción de los datos. También puede equilibrar los errores en conjuntos de datos en los que las clases están desequilibradas. Y lo que es más importante, puede manejar conjuntos de datos masivos con gran dimensionalidad. Sin embargo, una de las desventajas del uso de los bosques aleatorios es que puede sobreajustar fácilmente conjuntos de datos ruidosos, especialmente en el caso de hacer una regresión.

Boosting

Boosting es otro enfoque para mejorar las predicciones resultantes de un árbol de decisión. Al igual que el bagging y los bosques aleatorios, es un enfoque general que puede aplicarse a muchos métodos de aprendizaje estadístico para la regresión o la clasificación. Recordemos que el bagging implica la creación de múltiples copias del conjunto de datos de entrenamiento original utilizando el bootstrap, ajustando un árbol de decisión independiente a cada copia, y luego combinando todos los árboles con el fin de crear un único modelo de predicción. En particular, cada árbol se construye sobre un conjunto de datos bootstrap, independiente de los demás árboles.

El refuerzo funciona de forma similar, salvo que los árboles se cultivan secuencialmente: cada árbol se cultiva utilizando la información de los árboles cultivados anteriormente. El refuerzo no implica un muestreo bootstrap; en su lugar, cada árbol se ajusta a una versión modificada del conjunto de datos original.

Para los árboles de regresión y clasificación, el refuerzo funciona así:

• A diferencia de ajustar un solo árbol de decisión grande a los datos, lo que equivale a ajustar los datos con fuerza y potencialmente sobreajustar, el enfoque de refuerzo aprende lentamente.

• Dado el modelo actual, se ajusta un árbol de decisión a los residuos del modelo. Es decir, se ajusta un árbol utilizando los residuos actuales, en lugar del resultado $Y$, como respuesta.

• Entonces se añade este nuevo árbol de decisión a la función ajustada para actualizar los residuos. Cada uno de estos árboles puede ser bastante pequeño, con sólo unos pocos nodos terminales, determinados por el parámetro $d$ en el algoritmo. Al ajustar árboles pequeños a los residuos, se mejora lentamente $\hat{f}$ en las áreas en las que no funciona bien.

• El parámetro de encogimiento $\nu$ ralentiza aún más el proceso, permitiendo que más árboles y de diferentes formas ataquen a los residuos.

El boosting es muy útil cuando se tienen muchos datos y se espera que los árboles de decisión sean muy complejos. Boosting se ha utilizado para resolver muchos problemas de clasificación y regresión desafiantes, incluyendo el análisis de riesgo, el análisis de sentimiento, la publicidad predictiva, el modelado de precios, la estimación de ventas y el diagnóstico de pacientes, entre otros.

Árboles de decisión en R

Árboles de clasificación

Para esta parte, se trabaja con el conjunto de datos Carseats utilizando el paquete tree en R. Tenga en cuenta que necesita instalar los paquetes ISLR y tree en su entorno de R Studio primero. Carguemos primero el marco de datos Carseats del paquete ISLR.

library(ISLR)data(package="ISLR")carseats<-Carseats

Carguemos también el paquete tree.

require(tree)

El conjunto de datos Carseats es un marco de datos con 400 observaciones sobre las siguientes 11 variables:

• Ventas: ventas unitarias en miles

• PrecioComp: precio cobrado por el competidor en cada localidad

• Ingresos: nivel de ingresos de la comunidad en miles de dólares

• Publicidad: presupuesto de publicidad local en cada lugar en 1000s de dólares

• Población: población regional en miles

• Precio: precio de las plazas de coche en cada lugar

• DobleLoc: Malo, Bueno o Medio indica la calidad de la ubicación de las estanterías

• Edad: nivel de edad de la población

• Educación: nivel de educación en el lugar

• Urbano: Sí/No

• Estados Unidos: Sí/No

names(carseats)

Veamos el histograma de ventas de coches:

hist(carseats$Sales)

Observe que Sales es una variable cuantitativa. Se quiere demostrar utilizando árboles con una respuesta binaria. Para ello, se convierte Sales en una variable binaria, que se llamará High. Si la venta es menor que 8, será no alta. En caso contrario, será alta. Entonces puedes poner esa nueva variable High de nuevo en el marco de datos.

High = ifelse(carseats$Sales<=8, "No", "Yes")carseats = data.frame(carseats, High)

Ahora vamos a llenar un modelo usando árboles de decisión. Por supuesto, no puedes tener la variable Sales aquí porque tu variable de respuesta High fue creada a partir de Sales. Por lo tanto, excluyámosla y encajemos el árbol.

tree.carseats = tree(High~.-Sales, data=carseats)

Veamos el resumen de tu árbol de clasificación:

summary(tree.carseats)

Puedes ver las variables involucradas, el número de nodos terminales, la desviación media residual, así como la tasa de error de clasificación. Para hacerlo más visual, vamos a trazar el árbol también, y luego anotarlo utilizando la práctica función text:

plot(tree.carseats)text(tree.carseats, pretty = 0)

Hay muchas variables, lo que hace que sea muy complicado mirar el árbol. Al menos, puedes ver que en cada uno de los nodos terminales, están etiquetados como Yes o No. En cada nodo de división, se muestran las variables y el valor de la elección de la división (por ejemplo, Price < 92.5 o Advertising < 13.5).

Para obtener un resumen detallado del árbol, basta con imprimirlo. Le será útil si desea extraer detalles del árbol para otros fines:

tree.carseats

Es hora de podar el árbol. Vamos a crear un conjunto de entrenamiento y uno de prueba dividiendo el marco de datos carseats en 250 muestras de entrenamiento y 150 de prueba. En primer lugar, se establece una semilla para que los resultados sean reproducibles. A continuación, se toma una muestra aleatoria de los números de identificación (índice) de las muestras. En concreto, se toma una muestra del conjunto de 1 a n filas de asientos de coche, que es de 400. Quieres una muestra de tamaño 250 (por defecto, la muestra utiliza sin reemplazo).

set.seed(101)train=sample(1:nrow(carseats), 250)

Así que ahora obtienes este índice de train, que indexa 250 de las 400 observaciones. Usted puede volver a ajustar el modelo con tree, utilizando la misma fórmula, excepto decirle al árbol para utilizar un subconjunto es igual a train. Entonces hagamos un gráfico:

tree.carseats = tree(High~.-Sales, carseats, subset=train)plot(tree.carseats)text(tree.carseats, pretty=0)

El gráfico se ve un poco diferente debido al conjunto de datos ligeramente diferente. Sin embargo, la complejidad del árbol parece más o menos la misma.

Ahora vas a tomar este árbol y predecirlo en el conjunto de prueba, utilizando el método predict para árboles. Aquí querrás predecir realmente las etiquetas class.

tree.pred = predict(tree.carseats, carseats, type="class")

Entonces puedes evaluar el error utilizando una tabla de clasificación errónea.

with(carseats, table(tree.pred, High))

En las diagonales están las clasificaciones correctas, mientras que fuera de las diagonales están las incorrectas. Sólo quieres recuperar las correctas. Para ello, puede tomar la suma de las 2 diagonales dividido por el total (150 observaciones de prueba).

(72 + 43) / 150

Ok, se obtiene un error de 0,76 con este árbol.

Al crecer un árbol grande y tupido, podría tener demasiada varianza. Por lo tanto, vamos a utilizar la validación cruzada para podar el árbol de manera óptima. Usando cv.tree, usarás el error de clasificación errónea como base para hacer la poda.

cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)cv.carseats

Imprimir los resultados muestra los detalles de la ruta de la validación cruzada. Puede ver los tamaños de los árboles a medida que se podan, las desviaciones a medida que se realiza la poda, así como el parámetro de complejidad de costes utilizado en el proceso.

Realicemos un gráfico de esto:

plot(cv.carseats)

Mirando el gráfico, se ve una parte de espiral descendente debido al error de clasificación errónea en 250 puntos de validación cruzada. Así que vamos a elegir un valor en los pasos hacia abajo (12). A continuación, vamos a podar el árbol a un tamaño de 12 para identificar ese árbol. Por último, vamos a trazar y anotar ese árbol para ver el resultado.

prune.carseats = prune.misclass(tree.carseats, best = 12)plot(prune.carseats)text(prune.carseats, pretty=0)

Es un poco más superficial que los árboles anteriores, y realmente puede leer las etiquetas. Vamos a evaluarlo en el conjunto de datos de prueba de nuevo.

tree.pred = predict(prune.carseats, carseats, type="class")with(carseats, table(tree.pred, High))

(74 + 39) / 150

Parece que las clasificaciones correctas bajaron un poco. Ha hecho más o menos lo mismo que su árbol original, por lo que la poda no hizo mucho daño con respecto a los errores de clasificación errónea, y dio un árbol más simple.

En muchos casos, los árboles no dan muy buenos errores de predicción, así que vamos a echar un vistazo a los bosques aleatorios y al boosting, que tienden a superar a los árboles en lo que respecta a la predicción y a la clasificación errónea.

Bosques aleatorios

Para esta parte, utilizarás el Boston housing data para explorar los bosques aleatorios y el boosting. El conjunto de datos se encuentra en el paquete MASS. Proporciona los valores de las viviendas y otras estadísticas en cada uno de los 506 suburbios de Boston basados en un censo de 1970.

library(MASS)data(package="MASS")boston<-Bostondim(boston)names(boston)

Carguemos también el paquete randomForest.

require(randomForest)

Para preparar los datos para el bosque aleatorio, vamos a establecer la semilla y crear un conjunto de entrenamiento de muestra de 300 observaciones.

set.seed(101)train = sample(1:nrow(boston), 300)

En este conjunto de datos, hay 506 suburbios de Boston. Para cada surburb, tienes variables como el crimen per cápita, los tipos de industria, el promedio de habitaciones por vivienda, la proporción promedio de edad de las casas, etc. Utilicemos medv – el valor medio de las viviendas ocupadas por sus propietarios para cada uno de estos suburbios, como variable de respuesta.

Ajustemos un bosque aleatorio y veamos su rendimiento. Como se ha dicho, se utiliza la respuesta medv, la mediana del valor de la vivienda (en dólares $1K), y el conjunto de muestras de entrenamiento.

rf.boston = randomForest(medv~., data = boston, subset = train)rf.boston

La impresión del bosque aleatorio da su resumen: el número de árboles (500 fueron cultivados), la media de los residuos al cuadrado (MSR), y el porcentaje de varianza explicada. La MSR y el % de varianza explicada se basan en las estimaciones fuera de bolsa, un dispositivo muy inteligente en los bosques aleatorios para obtener estimaciones de error honestas.

El único parámetro de ajuste en un bosque aleatorio es el argumento llamado mtry, que es el número de variables que se seleccionan en cada división de cada árbol cuando se hace una división. Como se ve aquí, mtry es 4 de las 13 variables exploratorias (excluyendo medv) en los datos de Viviendas de Boston – lo que significa que cada vez que el árbol llega a dividir un nodo, 4 variables serían seleccionadas al azar, entonces la división se limitaría a 1 de esas 4 variables. Así es como randomForests descorrelaciona los árboles.

Vas a ajustar una serie de bosques aleatorios. Hay 13 variables, así que vamos a hacer que mtry vaya de 1 a 13:

• Para registrar los errores, estableces 2 variables oob.err y test.err.

• En un bucle de mtry de 1 a 13, primero ajustas el randomForest con ese valor de mtry en el conjunto de datos train, restringiendo el número de árboles a 350.

• Luego se extrae el error cuadrático medio del objeto (el error fuera de bolsa).

• Luego se predice en el conjunto de datos de prueba (boston) utilizando fit (el ajuste de randomForest).

• Por último, calculas el error de la prueba: el error medio cuadrático, que es igual a mean( (medv - pred) ^ 2 ).

oob.err = double(13)test.err = double(13)for(mtry in 1:13){ fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350) oob.err = fit$mse pred = predict(fit, boston) test.err = with(boston, mean( (medv-pred)^2 ))}

Básicamente acabas de cultivar 4550 árboles (13 veces 350). Ahora vamos a hacer un gráfico utilizando el comando matplot. El error de prueba y el error fuera de bolsa se unen para hacer una matriz de 2 columnas. Hay algunos otros argumentos en la matriz, incluyendo los valores de los caracteres de trazado (pch = 23 significa diamante relleno), los colores (rojo y azul), el tipo es igual a ambos (trazando ambos puntos y conectándolos con las líneas), y el nombre del eje y (Error Medio Cuadrado). También puede poner una leyenda en la esquina superior derecha de la trama.

matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))

En realidad, estas 2 curvas deben alinearse, pero parece que el error de la prueba es un poco más bajo. Sin embargo, hay mucha variabilidad en estas estimaciones de error de prueba. Dado que la estimación del error fuera de bolsa se calculó en un conjunto de datos y la estimación del error de prueba se calculó en otro conjunto de datos, estas diferencias están bastante bien dentro de los errores estándar.

¿Nota que la curva roja está suavemente por encima de la curva azul? Estas estimaciones de error están muy correlacionadas, porque el randomForest con mtry = 4 es muy similar al de mtry = 5. Por eso cada una de las curvas es bastante suave. Lo que se ve es que mtry alrededor de 4 parece ser la opción más óptima, al menos para el error de prueba. Este valor de mtry para el error fuera de bolsa es igual a 9.

Así que con muy pocos niveles, has ajustado un modelo de predicción muy potente usando bosques aleatorios. ¿Cómo es eso? El lado izquierdo muestra el rendimiento de un solo árbol. El error cuadrático medio fuera de la bolsa es de 26, y lo has reducido a unos 15 (un poco más de la mitad). Esto significa que has reducido el error a la mitad. Del mismo modo, para el error de la prueba, has reducido el error de 20 a 12.

Boosting

Comparado con los bosques aleatorios, el boosting hace crecer árboles más pequeños y rechonchos y va al sesgo. Vas a utilizar el paquete GBM (Gradient Boosted Modeling), en R.

require(gbm)

GBM pide la distribución, que es gaussiana, porque vas a hacer pérdida de error al cuadrado. Usted va a pedir GBM para 10.000 árboles, que suena como un montón, pero estos van a ser los árboles de poca profundidad. La profundidad de la interacción es el número de divisiones, por lo que quieres 4 divisiones en cada árbol. La contracción es 0,01, que es lo mucho que va a reducir el paso del árbol hacia atrás.

boost.boston = gbm(medv~., data = boston, distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)summary(boost.boston)

La función summary da una parcela de importancia variable. Parece que hay 2 variables que tienen alta importancia relativa: rm (número de habitaciones) y lstat (porcentaje de personas de menor nivel económico en la comunidad). Vamos a representar estas 2 variables:

plot(boost.boston,i="lstat")plot(boost.boston,i="rm")

El primer gráfico muestra que cuanto mayor es la proporción de personas de bajo nivel económico en el barrio, menor es el valor de los precios de la vivienda. El 2º gráfico muestra la relación inversa con el número de habitaciones: el número medio de habitaciones de la vivienda aumenta a medida que aumenta el precio.

Es hora de predecir un modelo reforzado en el conjunto de datos de prueba. Veamos el rendimiento de la prueba en función del número de árboles:

• Primero, se hace una cuadrícula de número de árboles en pasos de 100 desde 100 hasta 10.000.

• A continuación, se ejecuta la función predict sobre el modelo potenciado. Toma n.trees como argumento, y produce una matriz de predicciones sobre los datos de prueba.

• Las dimensiones de la matriz son 206 observaciones de prueba y 100 vectores de predicción diferentes en los 100 valores diferentes del árbol.

  n.trees = seq(from = 100, to = 10000, by = 100)predmat = predict(boost.boston, newdata = boston, n.trees = n.trees)dim(predmat)

Es hora de calcular el error de prueba para cada uno de los vectores de predicción:

• predmat es una matriz, medv es un vector, por lo tanto (predmat – medv) es una matriz de diferencias. Puedes utilizar la función apply para las columnas de estas diferencias cuadradas (la media). Eso calcularía el error cuadrático medio de las columnas para los vectores de predicción.

• Entonces haces un gráfico usando parámetros similares a los usados para Random Forest. Se mostraría un gráfico de error de refuerzo.

  boost.err = with(boston, apply( (predmat - medv)^2, 2, mean) )plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")abline(h = min(test.err), col = "red")

El error de refuerzo disminuye bastante a medida que aumenta el número de árboles. Esto es una prueba que demuestra que el boosting es reacio al sobreajuste. Incluyamos también en el gráfico el mejor error de prueba del randomForest. Boosting realmente consigue una cantidad razonable por debajo del error de prueba de randomForest.

Conclusión

Así que este es el final de este tutorial de R sobre la construcción de modelos de árboles de decisión: árboles de clasificación, bosques aleatorios y árboles potenciados. Los 2 últimos son métodos potentes que puedes utilizar en cualquier momento según sea necesario. En mi experiencia, boosting suele superar a RandomForest, pero éste es más fácil de implementar. En RandomForest, el único parámetro de ajuste es el número de árboles; mientras que en boosting, se requieren más parámetros de ajuste además del número de árboles, incluyendo la contracción y la profundidad de la interacción.

Si quieres aprender más, asegúrate de echar un vistazo a nuestro curso de Machine Learning Toolbox para R.