Comenzamos el estudio de las ecuaciones diferenciales parciales con el problema del flujo de calor en una barra uniforme de longitud \(L\), situada en el eje \(x\) con un extremo en el origen y el otro en \(x = L\) (Figura \(\PageIndex{1})).
Suponemos que la barra está perfectamente aislada, excepto posiblemente en sus extremos, y que la temperatura es constante en cada sección transversal y, por tanto, sólo depende de \(x\) y \(t\). También suponemos que las propiedades térmicas de la barra son independientes de \(x\) y \(t\). En este caso, se puede demostrar que la temperatura \(u = u(x, t)\) en el tiempo \(t\) en un punto \(x\) unidades desde el origen satisface la ecuación diferencial parcial
\
donde \(a\) es una constante positiva determinada por las propiedades térmicas. Se trata de la ecuación del calor.
Para determinar \(u\), debemos especificar la temperatura en cada punto de la barra cuando \(t=0\), digamos
\
Lo llamamos condición inicial. También debemos especificar las condiciones de contorno que debe satisfacer \(u\) en los extremos de la barra para todo \(t>0\). Llamaremos a este problema un problema de valor inicial-límite.
Empezamos con las condiciones de contorno \(u(0,t)=u(L,t)=0\), y escribimos el problema de valor inicial-límite como
\
Nuestro método para resolver este problema se llama separación de variables (no confundir con el método de separación de variables utilizado en la sección 2.2 para resolver ecuaciones diferenciales ordinarias). Empezamos por buscar funciones de la forma
\️ que no sean idénticas a cero y que satisfagan
\️
para todo \️((x,t)\️). Puesto que
\
(v_t=a^2v_{xx}\) si y sólo si
\
que reescribimos como
\
Dado que la expresión de la izquierda es independiente de \(x\) mientras que la de la derecha es independiente de \(t\), esta ecuación puede ser válida para todo \((x,t)\Nsólo si los dos lados son iguales a la misma constante, que llamamos constante de separación, y la escribimos como \(-\lambda\); por tanto,
\
Esto equivale a
\
y
\
Dado que \(v(0,t)=X(0)T(t)=0\) y \(v(L,t)=X(L)T(t)=0\) y no queremos que \(T\) sea idénticamente cero, \(X(0)=0\) y \(X(L)=0\). Por lo tanto, \(\lambda\) debe ser un valor propio del problema de valor límite
\
y \(X\) debe ser una función propia de \(\lambda\). A partir del teorema 11.1.2, los valores propios de la ecuación \ref{req:12.1.3} son \(\lambda_n=n^2\pi^2/L^2\), con las funciones propias asociadas
\
Sustituyendo (\lambda=n^2\pi^2/L^2\) en la ecuación \ref{req:12.1.2} da como resultado que
tiene la solución
Ahora dejemos que
Dado que
(v_n\) satisface la ecuación \ref{ec:12.1.1} con \(f(x)=\Nsin n\pi x/L\). De forma más general, si \(\alpha_1,\dots,\alpha_m\) son constantes y
\
entonces \(u_m\) satisface la Ecuación \ref{eq:12.1.1} con
\dentro de
Esto motiva la siguiente definición.
Teorema \(\PageIndex{1})
La solución formal del problema de valor inicial-problema de valor límite
\Nde
es
\Ndonde
\Nde
es la serie sinusoidal de Fourier de \(f\) en \(\); es decir,
\
Empleamos el término «solución formal» en esta definición porque no es en general cierto que la serie infinita en la ecuación \ref{ec:12.1.5} realmente satisfaga todos los requisitos del problema de valor inicial-límite Ecuación \ref{eq:12.1.4} cuando lo hace, decimos que es una solución real de la Ecuación \ref{eq:12.1.4}.
Debido a las exponenciales negativas de la Ecuación \ref{ec:12.1.5}, \(u\) converge para todo \((x,t)\) con \(t>0\) (Ejercicio 12.1.54). Puesto que cada término de la ecuación \ref{c:12.1.5} satisface la ecuación del calor y las condiciones de contorno de la ecuación \ref{c:12.14}, \(u\) también tiene estas propiedades si \(u_t\) y \(u_{xx}\) pueden obtenerse diferenciando la serie en la Ecuación \ref{ec:12.1.5} término a término una vez con respecto a \(t\) y dos veces con respecto a \(x\), para \(t>0\). Sin embargo, no siempre es legítimo diferenciar una serie infinita término a término. El siguiente teorema da una condición suficiente útil para la legitimidad de la diferenciación término a término de una serie infinita. Omitimos la demostración.
Teorema \(\PageIndex{2})
Una serie infinita convergente
\
puede diferenciarse término a término en un intervalo cerrado \(\) para obtener
\
((\)donde las derivadas en \(z=z_1\) y \(z=z_2\) son unilateralessiempre que \(w_n’\) sea continua en \(\) y
\
donde \(M_1,\) \(M_2,\) …, \(M_n,\) …, son constantes tales que la serie \(\sum_{n=1}^\infty M_n\) converge.
El teorema \(\PageIndex{2}), aplicado dos veces con \(z=x\) y una vez con \(z=t\), muestra que \(u_{xx}\) y \(u_t\) pueden obtenerse diferenciando \(u\) término a término si \(t>0\) (Ejercicio 12.1.54). Por tanto, \(u\) satisface la ecuación del calor y las condiciones de contorno de la ecuación \ref{ec:12.1.4} para \(t>0\). Por lo tanto, dado que \(u(x,0)=S(x)\N para \N(0\le x\le L\), \N(u) es una solución real de la Ecuación \ref{ec:12.1.4} si y sólo si \(S(x)=f(x)\Npara \N(0\le x\le L\). A partir del Teorema 11.3.2, esto es cierto si \(f\) es continuo y suave a trozos en \(\), y \(f(0)=f(L)=0\).
En este capítulo definiremos soluciones formales de varios tipos de problemas. Cuando te pedimos que resuelvas este tipo de problemas, siempre nos referimos a que debes encontrar una solución formal.
Ejemplo \(\PageIndex{1})
Resuelve la ecuación \ref{{c:12.1.4} con \(f(x)=x(x^2-3Lx+2L^2)\N.)
Solución
Desde el ejemplo \) es
\
Por tanto
\
Si los dos extremos de la barra están aislados para que no pase el calor a través de ellos, entonces las condiciones de contorno son
\
Te dejamos (Ejercicio 12.1.1) utilizar el método de separación de variables y el Teorema 11.1.3 para motivar la siguiente definición.
Teorema \(\PageIndex{3}\)
La solución formal del problema de valor inicial-límite
\Nes
donde
\Nes la serie coseno de Fourier de \(f\) sobre \(;\) es decir,
\Nserá la serie del coseno de Fourier de
Ejemplo \N(\NIndex de página{2})
Resuelve la ecuación \Nref:12.1.6} con \(f(x)=x\).
Solución
Desde el ejemplo 11.3.1, la serie del coseno de Fourier de \(f\) sobre \(\) es
\Npor lo tanto
\Ndejaremos que (Ejercicio 12.1.2) utilizar el método de separación de variables y el Teorema 11.1.4 para motivar la siguiente definición.
Teorema \(\PageIndex{4}\)
La solución formal del problema de valor inicial-límite
\Nes
donde
\Nes la serie sinusoidal mixta de Fourier de \(f\) sobre \(;\), es decir,
\Nserá la serie del seno mixto de Fourier de \N(f) sobre \Nla página{3}\Nde
Resolver la ecuación \Nref:12.1.7} con \(f(x)=x\).
Solución
Del ejemplo 11.3.4, la serie sinusoidal mixta de Fourier de \(f\) en \(\) es
\
Por tanto
\
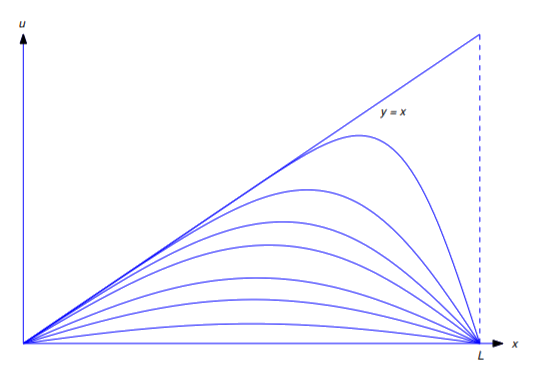
La figura \(\PageIndex{2}\) muestra una gráfica de (u=u(x,t)\) trazada con respecto a \(x\) para varios valores de \(t\). La línea \(y=x\) corresponde a \(t=0\). Las otras curvas corresponden a valores positivos de \(t\). A medida que \(t\) aumenta, las gráficas se aproximan a la recta \(u=0\).
Te dejamos (Ejercicio 12.1.3) que utilices el método de separación de variables y el Teorema 11.1.5 para motivar la siguiente definición.
Teorema \N(\PageIndex{5})
La solución formal del problema de valor inicial-problema de valor límite
\Nde
es
\Ndonde
\Nde
es la serie coseno de Fourier mixta de \N(f\) sobre \N(\); es decir,
\Nserá la serie del coseno de Fourier mixto de \N(f\N) en \N(\N).
Resuelve la ecuación \Nref:12.1.8} con \(f(x)=x-L\).
Solución
Del ejemplo 11.3.3, la serie mixta del coseno de Fourier de \(f\) en \(\) es
\Ndebido a ello
\Na que
\Nse trata de la solución de problemas de valor inicial-límite. En concreto, considere la solución formal
\
de la ecuación \ref{ec:12.1.4}, donde
\
es la serie sinusoidal de Fourier de \(f\) en \(\). Considere la \(m\)-ésima suma parcial
\
Para varios valores fijos de \(t\) (incluyendo \(t=0\)), grafique \(u_m(x,t)\) contra \(t\). En algunos casos puede ser útil graficar las curvas correspondientes a los distintos valores de \(t\) en los mismos ejes en otros casos puede querer graficar las distintas curvas sucesivamente (para valores crecientes de \(t\)), y crear una imagen de movimiento primitivo en su monitor. Repite este experimento para varios valores de \(m\), para comparar cómo dependen los resultados de \(m\) para valores pequeños y grandes de \(t\). Sin embargo, tenga en cuenta que los significados de «pequeño» y «grande» en este caso dependen de las constantes \(a^2\) y \(L^2\). Una buena manera de manejar esto es reescribir la ecuación \ref{eq:12.1.12} como
\
donde
\
y graficar \(u_m\) versus \(x\) para valores seleccionados de \tau\).
Estos comentarios también se aplican a las situaciones consideradas en los teoremas \(\PageIndex{3})-(\PageIndex{5}), excepto que la ecuación \ref{eq:12.1.13} debe ser sustituido por
\Nen los teoremas \N(\PageIndex{4}\N) y \N(\NPageIndex{5}\N).