Nous commençons l’étude des équations aux dérivées partielles par le problème du flux de chaleur dans une barre uniforme de longueur \(L\), située sur l’axe \(x\) avec une extrémité à l’origine et l’autre à \(x = L\) (figure \(\PageIndex{1}\)).
Nous supposons que la barre est parfaitement isolée, sauf éventuellement à ses extrémités, et que la température est constante sur chaque section transversale et ne dépend donc que de \(x\) et \(t\). Nous supposons également que les propriétés thermiques de la barre sont indépendantes de \(x\) et \(t\). Dans ce cas, on peut montrer que la température \(u = u(x, t)\) au temps \(t\) en un point \(x\) unités de l’origine satisfait l’équation différentielle partielle
\
où \(a\) est une constante positive déterminée par les propriétés thermiques. C’est l’équation de la chaleur.
Pour déterminer \(u\), nous devons spécifier la température en chaque point de la barre lorsque \(t=0\), disons
\
Nous appelons cela la condition initiale. Nous devons également spécifier les conditions aux limites que \(u\) doit satisfaire aux extrémités de la barre pour tout \(t>0\). Nous appellerons ce problème un problème initial-valeur limite.
Nous commençons par les conditions limites \(u(0,t)=u(L,t)=0\), et écrivons le problème initial-valeur limite comme
Notre méthode de résolution de ce problème est appelée séparation des variables (à ne pas confondre avec la méthode de séparation des variables utilisée dans la section 2.2 pour résoudre les équations différentielles ordinaires). Nous commençons par chercher des fonctions de la forme
\
qui ne sont pas identiquement nulles et satisfont
\
pour tout \((x,t)\). Puisque
\(v_t=a^2v_{xx}\) si et seulement si
que nous réécrivons comme
Puisque l’expression de gauche est indépendante de \(x\) alors que celle de droite est indépendante de \(t\), cette équation peut tenir pour tout \((x,t)\) seulement si les deux côtés sont égaux à la même constante, que nous appelons constante de séparation, et l’écrivons comme \(-\lambda\) ; ainsi,
Ceci est équivalent à
et
Puisque \(v(0,t)=X(0)T(t)=0\) et \(v(L,t)=X(L)T(t)=0\) et que nous ne voulons pas que \(T\) soit identiquement nul, \(X(0)=0\) et \(X(L)=0\). Par conséquent, \(\lambda\) doit être une valeur propre du problème de la valeur limite
\
et \(X\) doit être une fonction propre de \(\lambda\). D’après le théorème 11.1.2, les valeurs propres de l’équation \ref{eq:12.1.3} sont \(\lambda_n=n^2\pi^2/L^2\), avec les fonctions propres associées
\7816>
Substituant \(\lambda=n^2\pi^2/L^2\) dans l’équation \ref{eq:12.1.2} donne
qui a pour solution
Maintenant, laissons
Du fait que
\(v_n\) satisfait l’équation \ref{eq:12.1.1} avec \(f(x)=\sin n\pi x/L\). Plus généralement, si \(\alpha_1,\dots,\alpha_m\) sont des constantes et
\
alors \(u_m\) satisfait l’équation \ref{eq:12.1.1} avec
\
Cela motive la définition suivante.
Théorème \(\PageIndex{1}\)
La solution formelle du problème initial-initiale et limite
est
où
est la série sinusoïdale de Fourier de \(f\) sur \(\) ; c’est-à-dire,
\
Nous utilisons le terme « solution formelle » dans cette définition car il n’est pas en général vrai que la série infinie de l’équation \ref{eq :12.1.5} satisfasse effectivement toutes les exigences de l’équation \ref{eq:12.1.4} du problème de la valeur limite initiale lorsque c’est le cas, nous disons qu’il s’agit d’une solution réelle de l’équation \ref{eq:12.1.4}.
En raison des exponentielles négatives de l’équation \ref{eq:12.1.5}, \(u\) converge pour tous les \((x,t)\) avec \(t>0\) (Exercice 12.1.54). Puisque chaque terme de l’équation \ref{eq:12.1.5} satisfait l’équation de la chaleur et les conditions aux limites de l’équation \ref{eq:12.1.4}, \(u\) possède également ces propriétés si \(u_t\) et \(u_{xx}\) peuvent être obtenus en différenciant la série de l’équation \ref{eq:12.1.5} terme par terme une fois par rapport à \(t\) et deux fois par rapport à \(x\), pour \(t>0\). Cependant, il n’est pas toujours légitime de différencier une série infinie terme à terme. Le théorème suivant donne une condition suffisante utile pour la légitimité de la différenciation terme à terme d’une série infinie. Nous omettons la preuve.
Théorème \(\PageIndex{2}\)
Une série infinie convergente
\
peut être différenciée terme à terme sur un intervalle fermé \(\) pour obtenir
\((\)où les dérivées à \(z=z_1\) et \(z=z_2\) sont unilatérales.unilatérales\()\) à condition que \(w_n’\) soit continue sur \(\) et
\
où \(M_1,\) \(M_2,\) …, \(M_n,\) …, sont des constantes telles que la série \(\sum_{n=1}^\infty M_n\) converge.
Le théorème \(\PageIndex{2}\), appliqué deux fois avec \(z=x\) et une fois avec \(z=t\), montre que \(u_{xx}\) et \(u_t\) peuvent être obtenus en différenciant \(u\) terme à terme si \(t>0\) (Exercice 12.1.54). Par conséquent, \(u\) satisfait l’équation de la chaleur et les conditions aux limites de l’équation \ref{eq:12.1.4} pour \(t>0\). Par conséquent, puisque \(u(x,0)=S(x)\) pour \(0\le x\le L\), \(u\) est une solution réelle de l’équation \ref{eq:12.1.4} si et seulement si \(S(x)=f(x)\) pour \(0\le x\le L\). D’après le théorème 11.3.2, ceci est vrai si \(f\) est continue et lisse par morceaux sur \(\), et \(f(0)=f(L)=0\).
Dans ce chapitre, nous définirons les solutions formelles de plusieurs types de problèmes. Lorsque nous vous demandons de résoudre de tels problèmes, nous voulons toujours dire que vous devez trouver une solution formelle.
Exemple \(\PageIndex{1}\)
Résoudre l’équation \ref{eq:12.1.4} avec \(f(x)=x(x^2-3Lx+2L^2)\).
Solution
D’après l’exemple \) est
Donc
Si les deux extrémités de la barre sont isolées pour qu’aucune chaleur ne puisse les traverser, alors les conditions aux limites sont
Nous vous laissons le soin (exercice 12.1.1) d’utiliser la méthode de séparation des variables et le théorème 11.1.3 pour motiver la définition suivante.
Théorème \(\PageIndex{3}\)
La solution formelle du problème de valeur limite initiale
\
est
où
\
est la série cosinus de Fourier de \(f\) sur \( ;\) c’est-à-dire,
\
Exemple \(\PageIndex{2}\)
Solvons l’équation \ref{eq :12.1.6} avec \(f(x)=x\).
Solution
D’après l’exemple 11.3.1, la série cosinus de Fourier de \(f\) sur \(\) est
Donc
Nous vous laissons le soin (exercice 12.1.2) d’utiliser la méthode de séparation des variables et le théorème 11.1.4 pour motiver la définition suivante.
Théorème \(\PageIndex{4}\)
La solution formelle du problème de valeur limite initiale
\
est
où
\
est la série sinusoïdale de Fourier mixte de \(f\) sur \( ;\) c’est-à-dire,
Exemple \(\PageIndex{3}\)
Solvons l’équation \ref{eq :12.1.7} avec \(f(x)=x\).
Solution
D’après l’exemple 11.3.4, la série sinusoïdale de Fourier mixte de \(f\) sur \(\) est
\
Donc
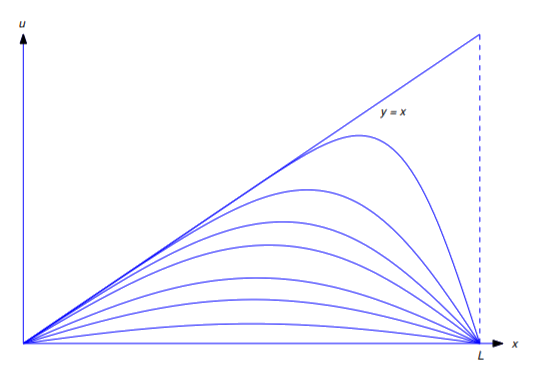
Figure \(\PageIndex{2}\) montre un graphique de \(u=u(x,t)\) tracé par rapport à \(x\) pour différentes valeurs de \(t\). La ligne \(y=x\) correspond à \(t=0\). Les autres courbes correspondent à des valeurs positives de \(t\). Lorsque \(t\) augmente, les graphes se rapprochent de la droite \(u=0\).
Nous vous laissons le soin (exercice 12.1.3) d’utiliser la méthode de séparation des variables et le théorème 11.1.5 pour motiver la définition suivante.
Théorème \(\PageIndex{5}\)
La solution formelle du problème des valeurs initiales-initiale et limite
est
où
est la série mixte de Fourier en cosinus de \(f\) sur \(\) ; c’est-à-dire,
Exemple \(\PageIndex{4}\)
Solvons l’équation \ref{eq :12.1.8} avec \(f(x)=x-L\).
Solution
D’après l’exemple 11.3.3, la série cosinus de Fourier mixte de \(f\) sur \(\) est
\
Therefore
\
Using Technology
Les expériences numériques peuvent améliorer votre compréhension des solutions des problèmes de valeurs limites initiales. Pour être spécifique, considérez la solution formelle
\
de l’équation \ref{eq:12.1.4}, où
\
est la série sinusoïdale de Fourier de \(f\) sur \(\). Considérez la \(m\)-ième somme partielle
Pour plusieurs valeurs fixes de \(t\) (y compris \(t=0\)), tracez le graphique \(u_m(x,t)\) en fonction de \(t\). Dans certains cas, il peut être utile de tracer les courbes correspondant aux différentes valeurs de \(t\) sur les mêmes axes ; dans d’autres cas, vous pouvez tracer les différentes courbes successivement (pour des valeurs croissantes de \(t\)), et créer une image animée primitive sur votre moniteur. Répétez cette expérience pour plusieurs valeurs de \(m\), afin de comparer la façon dont les résultats dépendent de \(m\) pour les petites et grandes valeurs de \(t\). Cependant, gardez à l’esprit que les significations de « petit » et « grand » dans ce cas dépendent des constantes \(a^2\) et \(L^2\). Une bonne façon de gérer cela est de réécrire l’équation \ref{eq:12.1.12} sous la forme
\
où
\
et de représenter graphiquement \(u_m\) en fonction de \(x\) pour des valeurs sélectionnées de \(\tau\).
Ces commentaires s’appliquent également aux situations considérées dans les théorèmes \(\PageIndex{3}\)-\(\PageIndex{5}\), sauf que l’équation \ref{eq:12.1.13} doit être remplacée par
\
dans les Théorèmes \(\PageIndex{4}\) et \(\PageIndex{5}\).