Il y a quelques mois, je suis allée à une session d’origami créatif à l’heure du déjeuner, organisée par des personnes adorables au $WORK. J’avais fait un peu d’origami quand j’étais plus jeune, mais surtout des grenouilles et des grues, qui m’ont depuis aidé à passer les heures quand je surveillais des examens. Cependant, lors de cette session de midi, on m’a montré comment faire de l’origami modulaire. Cela implique de faire beaucoup de pièces d’origami (généralement assez simples), puis de les emboîter pour faire des structures plus grandes.

Je suis rentré chez moi avec une simple boule Sonobe de 12 unités cet après-midi-là et j’étais très content de moi.

Origami modulaire d’entrée de gamme : la boule Sonobe de 12 unités. Mathématiquement, c’est un octaèdre cumulé ; pratiquement, c’est 12 feuilles de papier carré et environ 1 heure de votre temps.
Les choses se sont plutôt intensifiées à partir de là.

Entre l’exécution de certaines de ces sessions de midi moi-même maintenant, et être demandé à plusieurs reprises sur Twitter sur la façon dont je fais les jolies choses que je continue à tweeter, j’ai pensé qu’il serait utile de mettre en place un guide rapide (ou une ferme de liens, au moins).
Les unités Sonobe sont très faciles à plier, assez indulgentes, et peuvent être utilisées pour faire un cube (6 unités), un octaèdre cumulé (12 unités), un icosaèdre cumulé (30), et une sorte d’icosaèdre tronqué (90, en gros un ballon de football à pointes). Ils constituent une assez bonne introduction aux principes généraux :

Famille Sonobe : 90, 30, 12, 6 et 3 unités. Celui à 3 unités est une bipyramide trigonale mais compte à peine ! Elles ont toutes été réalisées avec l’unité légèrement modifiée mentionnée ci-dessous. Celui de 90 unités est le plus grand Sonobe qui vaut vraiment la peine d’être fabriqué IMHO : environ 3 heures de travail
La boule de 30 unités a les symétries d’un icosaèdre (ou dodécaèdre). Une fois que vous avez appris à construire cet objet en modules Sonobe, vous avez essentiellement appris à construire n’importe quelle boule d’origami modulaire de 30 unités : il s’agit surtout de fendre 30 unités d’arêtes en groupes de trois pour former les 12 faces pentagonales d’un dodécaèdre (ou de manière équivalente/alternative, de les fendre en groupes de cinq pour former les 20 faces triangulaires d’un icosaèdre – la différence est surtout une question de perspective).

Icosaèdre cumulé composé d’unités Sonobe : 30 feuilles de papier, et – si vous avez pris le coup de main avec la boule de 12 unités – encore seulement 1 heure de votre temps
Il y a beaucoup de variations sur l’unité Sonobe que vous pouvez (ré)inventer, en ajoutant des pliages arrière qui exposent l’autre côté du papier, ou qui rendent les onglets plus étroits que les poches, donnant un aspect plus complexe.

Icosaèdre cumulé fait d’unités Sonobe légèrement modifiées
Bien que la structure de 90 unités soit assez stable, la suivante (270 unités) a tendance à s’affaisser sous son propre poids avec le temps, mais à ce stade, cela semblait être un droit de passage d’en fabriquer une.

9 heures de construction, plus un peu de planification. Cela utilise du papier duo, qui est coloré sur les deux côtés, et une unité Sonobe modifiée qui a un pliage inversé pour exposer l’autre côté du papier dans chaque module.
Les unités Sonobe peuvent aussi être assemblées à l’envers pour faire des polyèdres cumulés vers l’intérieur…

Faire entrer les dernières unités sur la boule inversée (à gauche) est délicat.
…et elles peuvent aussi être assemblées par paires puis assemblées en un dodécaèdre pentakis à pointes….

Pentakis dodécaèdre, avec une unité Sonobe à pliage inversé qui montre l’autre côté du papier.
…et d’autres structures.

Le site ci-dessus décrit cela comme un triacontaèdre rhombique, mais je suis presque sûr que ce n’est pas le cas. Je ne suis pas sûr de ce que c’est réellement cependant. Possède à la fois un changement de couleur et les unités sont assemblées » à l’envers » pour le rendre cumulé vers l’intérieur.
L’unité suivante que j’ai essayée était l’unité du Penultimate edge (attribuée à Robert Neal), qui peut être utilisée pour faire un dodécaèdre filaire, comme l’a démontré Matt Parker, le mathématicien de stand-up. D’autres variations de cette sous-unité peuvent être utilisées pour faire à peu près n’importe quel autre polyèdre filaire.

Dodecahedron. J’essayais d’utiliser le papier coloré ennuyeux sur celui-ci, mais j’ai assez aimé le résultat à la fin !
L’unité de bord PhiZZ de Thomas Hull fait des structures filaires similaires, mais les modules s’emboîtent plus étroitement et les structures résultantes sont beaucoup plus robustes que ce que vous obtenez avec les avant-derniers modules.

Icosaèdre tronqué – c’est fondamentalement la forme d’un ballon de football (12 pentagones, entourés d’hexagones) et de certaines capsides virales aussi.
Vous pouvez également faire des variantes de changement de couleur en utilisant la technique montrée dans les boîtes de décoration de Lewis Simon.

Dodécaèdre réalisé à partir d’unités PHiZZ avec un changement de couleur.
Pour les structures basées sur des dodécaèdres/icosaèdres et réalisées à partir d’unités d’arêtes, vous pouvez toujours vous en sortir en utilisant seulement trois couleurs et ne jamais avoir deux pièces de la même couleur qui se touchent. En effet, vous pouvez dessiner un circuit hamiltonien sur un dodécaèdre : c’est un chemin de sommet à sommet qui ne visite chaque sommet qu’une seule fois et qui revient à son point de départ. On peut représenter cela en 2D sur un diagramme de Schlegel.
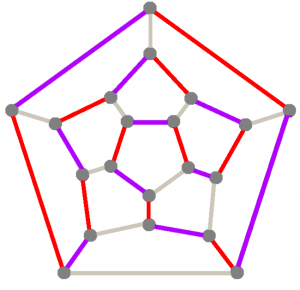
Circuit hamiltonien à travers le diagramme de Schlegel d’un dodécaèdre . Les arêtes rouges et violettes forment le circuit hamiltonien ; les arêtes grises sont ce qui reste. Vous remarquerez que chaque sommet possède une arête de chacune des trois couleurs. Le diagramme est une projection d’un dodécaèdre : imaginez que vous prenez une image filaire du dodécaèdre et que vous l’illuminez avec une torche : le diagramme de Schlegel est l’ombre 2D que ce polyèdre 3D projette sur le mur. Il est assez facile de déterminer quelle arête du diagramme 2D correspond à quelle arête de la chose que vous construisez.
Si vous coloriez les arêtes alternées du circuit hamiltonien dans deux des couleurs que vous avez choisies, et le reste des arêtes dans la troisième, alors vous éviterez tout conflit de couleurs. Je n’ai appris cela qu’après avoir commencé à réaliser ces structures, donc toutes n’ont pas cette coloration optimale ! La même règle des 3 couleurs est vraie pour les autres solides de Platon, et aussi pour l’icosaèdre tronqué.
Le kusudama des trous d’étoile de Francesco Mancini utilise un module similaire au PHiZZ, mais avec un petit coude arrière qui donne un bel effet d’étoile en 3D. Celui-ci est en forme de dodécaèdre (30 unités), mais un icosaèdre tronqué de 90 unités devrait également être possible.

Dodécaèdre à trous d’étoiles.
Mise à jour : oui, c’est possible 🙂

Icosaèdre tronqué à trous d’étoile
L’unité de bord de triangle de Lewis Simon et Bennett Arnstein peut être utilisée pour faire de très beaux tétraèdres, octaèdres et icosaèdres en patchwork.

Icosaèdre.
Ils sont un peu bricolés à assembler mais sont très robustes une fois construits. Un effet de patchwork similaire pour le dodécaèdre peut être obtenu avec le module parapluie de M. Mukhopadhyay ; les unités Sonobe peuvent être utilisées pour faire des cubes analogues de style gâteau de Battenberg.

Solides platoniques de type Battenberg-cake. Le dodécaèdre est fabriqué à partir d’unités parapluie ; le cube à partir de Sonobe. Le tétraèdre, l’octaèdre et l’icosaèdre sont tous réalisés à partir de modules d’arêtes de triangles.
L’unité simple de triangle isocèle (attribuée diversement à M. Mukhopadhyay, Jeannine Mosely et Roberto Morassi) peut être utilisée pour réaliser des petits et grands dodécaèdres stellaires.

Grand (à gauche) et petit (à droite) dodécaèdre stellaire.
Le petit dodécaèdre stellaire est particulièrement agréable et constitue une décoration assez robuste s’il est réalisé en papier pelliculé.

Décs de Noël
Le grand dodécaèdre étoilé peut être réalisé à partir de la même sous-unité, mais il est plus délicat à construire car une languette doit s’enrouler dans une poche qui se trouve en partie à l’intérieur de la languette ronde suivante. J’ai utilisé des pinces à bec d’aiguille pour le construire, et je ne suis toujours pas terriblement satisfait du résultat.
L’inverse est vrai pour le module étoile de Paolo Bascetta, qui fait un grand grand dodécaèdre stellaire, mais une petite stellation plutôt *eh*. Ce module a besoin de papier duo (c’est-à-dire de papier coloré des deux côtés) pour un meilleur effet.

Grand (à gauche) et petit (à droite) dodécaèdre stellaire.
Le module Electra de Dave Mitchell peut être utilisé pour faire un icosidodécaèdre : il est inhabituel en ce que chaque module correspond à un sommet de la structure : les unités d’arêtes décrites jusqu’à ce point se combinent ensemble pour faire chaque sommet.

Icosidodécaèdre réalisé à partir de modules Electra
Je ne suis pas très content de mon kusudama Void (Tadashi Mori) : J’aurais dû utiliser du papier duo, mais c’était vraiment délicat à assembler. Peut-être un jour. C’est l’une des rares structures ici qui est revenue à la structure originale octaédrique/cubique à 12 unités. Je ne suis pas sûr que la version à 30 unités serait stable.

Vide octaédrique
Mise à jour : Ouais, je ne pense pas que la version à 30 unités soit faisable. Je pense que les unités sont trop larges pour entrer réellement dans un icosaèdre : Je n’ai même pas pu le faire avec de la colle, donc je ne pense pas que ce soit juste un problème de stabilité. Cependant, j’ai fait une meilleure version à 12 unités, avec du papier duo et un petit pli inversé sur le bord extérieur pour exposer correctement la deuxième couleur, dont je suis assez satisfait :

Vide octaédrique (modifié)
Les petits modules tortue de Tomoko Fusè sont extrêmement flexibles : ils peuvent être utilisés pour faire à peu près n’importe quel polyèdre qui est fait de polygones réguliers. Cependant, comme les rabats n’ont qu’une seule couche de papier, ils ne s’emboîtent pas terriblement bien, et je ne les ai trouvés assez robustes que pour faire de petites structures sans l’aide de colle. Cependant, avec de la colle, j’ai fait un rhombicosidodécaèdre, qui est cool parce qu’il est construit de pentagones, de triangles et de carrés (tous les polygones que l’on trouve dans les solides de Platon)…

Le rhombicosidodécaèdre impossible à épeler.
…et aussi une paire de snub-cubes, qui sont encore plus intéressants car le snub-cube a deux images miroir non superposables, comme les mains, les acides aminés et les amphétamines.

Snubcubes : énatiomorphes gauchers et droitiers.
J’ai trouvé le kusudama Etna de Maria Sinayskaya dans le livre Exquisite Modular Origami de Meenakshi Mukerji. C’est un modèle vraiment joli, et robuste une fois assemblé, mais il peut être un peu félin pendant la construction : J’ai utilisé de très petites pinces à linge pour le maintenir ensemble au fur et à mesure que je le fabriquais.

Etna kusudama.
Le composé de cinq octaèdres de Meenakshi Mukerji (inspiré par Dennis Walker) est aussi un peu fally-aparty, mais je l’aime bien car – contrairement à beaucoup de ces modèles – c’est véritablement le polyèdre ainsi nommé, plutôt que quelque chose où vous devez loucher sur les trous dans le cadre filaire et y imaginer des faces.

Composé de cinq octaèdres. Vous pouvez facilement voir l’octaèdre jaune ici : le sixième pic est sous le modèle ; les quatre autres couleurs sont entrelacées de façon similaire.
Les cinq tétraèdres entrecroisés sont en fait beaucoup plus faciles à réaliser qu’il n’y paraît. Les modules à 6 degrés de Francis Ow eux-mêmes sont faciles à plier, et les sommets sont beaucoup plus robustes qu’il n’y paraît. Le plus difficile est de relier les modules entre eux de la bonne façon. J’y suis parvenu deux fois, mais seulement en regardant la vidéo YouTube et en effectuant des gymnastiques assorties « violet = vert » dans ma tête.

Composé de cinq tétraèdres – pièce de fête.
La page de Michał Kosmulski a beaucoup de belles illustrations, d’instructions et d’inspirations. J’y ai trouvé l’icosadodécaèdre blintz de Tung Ken Lam (également crédité comme le modèle de plans sécants UVWXYZ de Francesco Mancini). Il présente la même symétrie que l’icosadodécaèdre Electra ci-dessus, mais on peut voir plus clairement les six pentagones qui se croisent. Les deux ont la même structure sous-jacente que la sphère de Hoberman – cette chose modèle de bâton en plastique qui se dilate/contracte bien-aimée des foires scientifiques.

UVWXYZ intersecting plane icosadodecahedron
Ce dernier est un peu une tricherie car (en théorie, et surtout en pratique aussi) les structures ci-dessus ne sont maintenues ensemble que par la friction. Le kusudama étoilé de fleurs révélées de Valentina Gonchar doit être collé, ce qui est un peu de la triche, mais je n’ai pas pu résister car c’est deux structures en une :

Étoile florale révélée – fermée (à gauche) et ouverte par pression (à droite).
Ce que j’aimerais encore faire :
- Construire une boule PhiZZ beaucoup plus grande (270 unités) : ce serait utile pour démontrer les structures des capsides virales. MISE À JOUR : Fait!

Avant…

…Après
- Je n’ai pas encore trouvé un bon modèle de grand dodécaèdre : ils existent sur Pintrest, mais je n’ai pas encore trouvé d’instructions pour un modèle. UPDATE : C’est fait ! (Je n’ai pas réussi à trouver comment faire les 3 couleurs, mais le module est de Saku B, recommandé par Nick dans les commentaires ci-dessous)

Grand dodécaèdre
- J’ai perdu l’endroit où j’avais trouvé les instructions pour ce triacontaèdre rhombique cumulé vers l’intérieur : J’aimerais bien les redécouvrir pour pouvoir créditer l’inventeur ! MISE À JOUR : ce n’est pas là que je l’ai vu à l’origine, mais AresMares de Gewre a un tutoriel vidéo, et un aimable commentateur m’a fait savoir que le concepteur est Silvana Betti Mamino – merci !

Triacontaèdre rhombique de source inconnue.
- Inventer mon propre module 🙂
.