• Équation de la régression logistique
• Courbes d’exemple de régression logistique
• Régression logistique – coefficient B
• Régression logistique – taille de l’effet
• . Coefficients B
• Régression logistique – Taille de l’effet
• Hypothèses de la régression logistique

La régression logistique est une technique pour prédire une
variable de résultat dichotomique à partir de prédicteurs 1+.Exemple : quelle est la probabilité que des personnes meurent avant 2020, compte tenu de leur âge en 2015 ? Notez que « mourir » est une variable dichotomique car elle n’a que 2 issues possibles (oui ou non).
Cette analyse est également connue sous le nom de régression logistique binaire ou simplement « régression logistique ». Une technique connexe est la régression logistique multinomiale qui prédit les variables de résultat avec 3+ catégories.

Régression logistique – Exemple simple

Une maison de retraite dispose de données sur le sexe, l’âge au 1er janvier 2015 de N = 284 clients et si le client est décédé avant le 1er janvier 2020. Les données brutes se trouvent dans ce Googlesheet, partiellement présenté ci-dessous.

D’abord, concentrons-nous uniquement sur l’âge : peut-on prédire le décès avant 2020 à partir de l’âge en 2015 ? Et -si oui- précisément comment ? Et dans quelle mesure ? Une bonne première étape consiste à inspecter un nuage de points comme celui présenté ci-dessous.

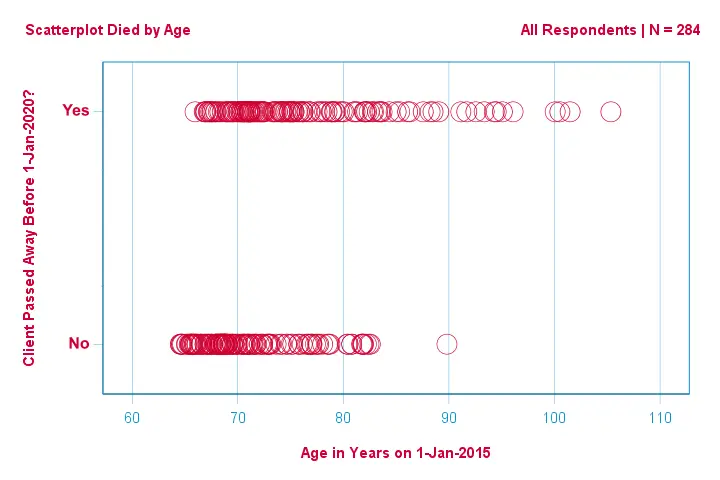
Les quelques éléments que nous voyons dans ce nuage de points sont les suivants

• tous les clients de plus de 83 ans, sauf un, sont décédés dans les 5 années suivantes;
• l’écart-type de l’âge est beaucoup plus important pour les clients qui sont décédés que pour les clients qui ont survécu;
• l’âge a une asymétrie positive considérable, en particulier pour les clients qui sont décédés.

Mais comment pouvons-nous prédire si un client est mort, étant donné son âge ? C’est ce que nous allons faire en ajustant une courbe logistique.

Équation de régression logistique simple

La régression logistique simple calcule la probabilité d’un certain résultat compte tenu d’une seule variable prédictive comme

$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}$

où

• \(P(Y_i)\) est la probabilité prédite que \(Y\) soit vrai pour le cas \(i\) 😉
• \(e\) est une constante mathématique d’environ 2.72;
• \(b_0\) est une constante estimée à partir des données;
• \(b_1\) est un coefficient b estimé à partir des données;
• \(X_i\) est le score observé sur la variable \(X\) pour le cas \(i\).

L’essence même de la régression logistique consiste à estimer \(b_0\) et \(b_1\). Ces 2 nombres nous permettent de calculer la probabilité de décès d’un client pour tout âge observé. Nous allons illustrer cela avec des exemples de courbes que nous avons ajoutées au nuage de points précédent.

Courbes d’exemple de régression logistique

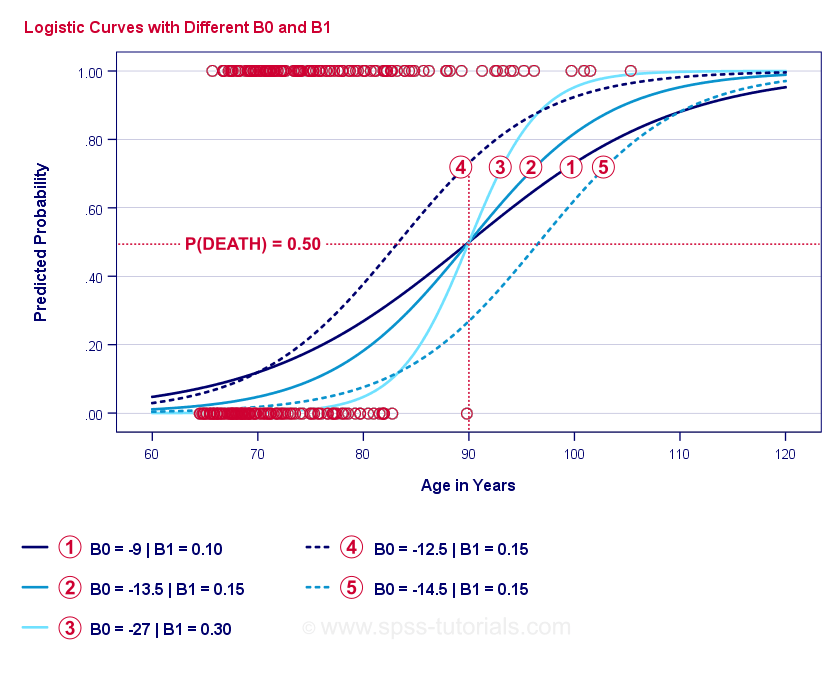
Si vous prenez une minute pour comparer ces courbes, vous pouvez constater ce qui suit :

• \(b_0\) détermine la position horizontale des courbes : lorsque \(b_0\) augmente, les courbes se déplacent vers la gauche mais leurs pentes ne sont pas affectées. C’est ce que l’on observe pour les courbes , et . Notez que \(b_0\) est différent mais \(b_1\) est égal pour ces courbes.
• A mesure que \(b_0\) augmente, les probabilités prédites augmentent également : étant donné l’âge = 90 ans, la courbe prédit une probabilité de décès d’environ 0,75. Les courbes et prédisent des probabilités de décès d’environ 0,50 et 0,25 pour un client de 90 ans.
• \(b_1\) détermine la pente des courbes : si \(b_1\) > 0, la probabilité de décès augmente avec l’âge. Cette relation devient plus forte lorsque \(b_1\) devient plus grand. Les courbes , et illustrent ce point : lorsque \(b_1\) devient plus grand, les courbes deviennent plus raides, donc la probabilité de mourir augmente plus rapidement avec l’âge.

Pour l’instant, il nous reste une question : comment trouver les  » meilleures  » \(b_0\) et \(b_1\) ?

Régression logistique – Probabilité logarithmique

Pour chaque répondant, un modèle de régression logistique estime la probabilité qu’un certain événement \(Y_i\) se soit produit. Évidemment, ces probabilités devraient être élevées si l’événement s’est effectivement produit et inversement. Une façon de résumer la performance d’un certain modèle pour tous les répondants est la log-vraisemblance \(LL\):

$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

où

• \(Y_i\) vaut 1 si l’événement s’est produit et 0 s’il ne s’est pas produit ;
• \(ln\) désigne le logarithme naturel : à quelle puissance doit-on élever \(e\) pour obtenir un nombre donné ?

\(LL\) est une mesure de la qualité de l’ajustement : toutes choses égales par ailleurs, un modèle de régression logistique s’ajuste mieux aux données dans la mesure où \(LL\) est plus grand. De manière assez déroutante, \(LL\) est toujours négatif. Nous voulons donc trouver les \(b_0\) et \(b_1\) pour lesquels
\(LL\) est aussi proche de zéro que possible.

Estimation du maximum de vraisemblance

Contrairement à la régression linéaire, la régression logistique ne peut pas facilement calculer les valeurs optimales de \(b_0\) et \(b_1\). Au lieu de cela, nous devons essayer différents nombres jusqu’à ce que \(LL\) n’augmente plus. Chacune de ces tentatives est appelée une itération. Le processus de recherche des valeurs optimales par le biais de telles itérations est connu sous le nom d’estimation du maximum de vraisemblance.

C’est donc essentiellement de cette manière que les logiciels statistiques -tels que SPSS, Stata ou SAS- obtiennent les résultats de la régression logistique. Heureusement, ils sont étonnamment bons dans ce domaine. Mais au lieu d’indiquer \(LL\), ces logiciels indiquent \(-2LL\).\NL’\(-2LL\) est une mesure de « mauvais ajustement » qui suit une distribution
chi-carré.\NCe qui rend \(-2LL\) utile pour comparer différents modèles comme nous le verrons bientôt. \(-2LL\) est désigné par -2 Log-vraisemblance dans le résultat présenté ci-dessous.

La note de bas de page ici nous indique que l’estimation du maximum de vraisemblance a nécessité seulement 5 itérations pour trouver les b-coefficients optimaux \(b_0\) et \(b_1\). Examinons donc ceux-ci maintenant.

Régression logistique – Coefficients B

La sortie la plus importante pour toute analyse de régression logistique sont les coefficients b. La figure ci-dessous les montre pour nos données d’exemple.

Avant d’entrer dans les détails, cette sortie montre brièvement

les b-coefficients qui composent notre modèle;
les erreurs standard pour ces b-coefficients;
la statistique de Wald -calculée comme \((\frac{B}{SE})^2\)- qui suit une distribution chi-carré ;
les degrés de liberté pour la statistique de Wald;
les niveaux de signification pour les b-coefficients;
les b-coefficients exponentiés ou \(e^B\) sont les odds ratios associés aux changements des scores des prédicteurs;
l’intervalle de confiance à 95% pour les b-coefficients exponentiés.

Les coefficients b complètent notre modèle de régression logistique, qui est maintenant

$P(décès_i) = \frac{1}{1 + e^{\,-\,(-9,079\,+\,0.124\, \cdot\, âge_i)}}$$

Pour un client de 75 ans, la probabilité de décéder dans les 5 ans est

$P(décès_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}=$$

$P(death_i) = \frac{1}{1 + e^{\,-\,0.249}}=$

$P(death_i) = \frac{1}{1 + 0.780}=$

$P(mort_i) \approximativement 0,562$

Donc maintenant nous savons comment prédire la mort dans les 5 ans étant donné l’âge de quelqu’un. Mais quelle est la qualité de cette prédiction ? Il y a plusieurs approches. Commençons par des comparaisons de modèles.

Régression logistique – Modèle de base

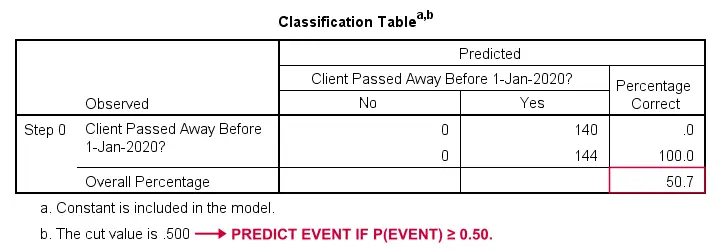
Comment pourrions-nous prédire qui est décédé si nous n’avions pas d’autres informations ? Eh bien, 50,7% de notre échantillon est décédé. Donc la probabilité prédite serait simplement de 0,507 pour tout le monde.

À des fins de classification, nous prédisons généralement qu’un événement se produit si p(événement) ≥ 0,50. Puisque p(mort) = 0,507 pour tout le monde, nous prédisons simplement que tout le monde est décédé. Cette prédiction est correcte pour les 50,7% de notre échantillon qui sont décédés.

Régression logistique – Rapport de vraisemblance

Maintenant, à partir de ces probabilités prédites et des résultats observés, nous pouvons calculer notre mesure de mauvais ajustement : -2LL = 393,65. Notre modèle réel – prédisant la mort par l’âge – donne -2LL = 354,20. La différence entre ces chiffres est connue comme le rapport de vraisemblance \(LR\) :

$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Important, \(LR\) suit une distribution chi-carré avec \(df\) degrés de liberté, calculée comme suit

$df = k_{model} – k_{baseline}$$

où \(k\) désigne le nombre de paramètres estimés par les modèles. Comme le montre ce Googlesheet, \(LR\) et \(df\) donnent un niveau de signification pour l’ensemble du modèle.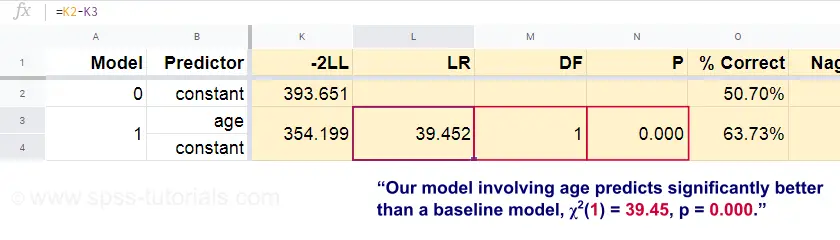

L’hypothèse nulle ici est qu’un modèle prédit aussi mal que le modèle de base dans une certaine population. Puisque p = 0,000, nous la rejetons : notre modèle (prédisant la mort à partir de l’âge) est significativement plus performant qu’un modèle de base sans aucun prédicteur.
Mais précisément combien meilleur ? On y répond par sa taille d’effet.

Régression logistique – Taille d’effet du modèle

Une bonne façon d’évaluer la performance de notre modèle est à partir d’une mesure de taille d’effet. Une option est le R2 de Cox & Snell ou \(R^2_{CS}\) calculé comme

$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-\,(-2LL_{baseline})}{n}}$

Malheureusement, \(R^2_{CS}\) n’atteint jamais son maximum théorique de 1. Par conséquent, une version ajustée connue sous le nom de Nagelkerke R2 ou \(R^2_{N}\) est souvent préférée :

$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}$

Pour les données de notre exemple, \(R^2_{CS}\) = 0,130 ce qui indique une taille d’effet moyenne. \(R^2_{N}\) = 0,173, ce qui est légèrement supérieur à la taille moyenne.

Enfin, \(R^2_{CS}\) et \(R^2_{N}\) sont techniquement complètement différents du carré r tel qu’il est calculé dans la régression linéaire. Cependant, elles tentent de remplir le même rôle. Les deux mesures sont donc connues comme des mesures de pseudo-carré r.

Régression logistique – Taille d’effet des prédicteurs

Oddinairement, très peu de manuels mentionnent une taille d’effet pour les prédicteurs individuels. C’est peut-être parce que ceux-ci sont complètement absents de SPSS. La raison pour laquelle nous en avons besoin est que les b-coefficients dépendent des échelles (arbitraires) de nos prédicteurs : si nous entrions l’âge en jours au lieu d’années, son b-coefficient diminuerait énormément. Cela rend évidemment les b-coefficients impropres à la comparaison des prédicteurs au sein ou entre différents modèles.
JASP inclut des b-coefficients partiellement normalisés : les prédicteurs quantitatifs -mais pas la variable de résultat- sont entrés comme des z-scores comme indiqué ci-dessous.

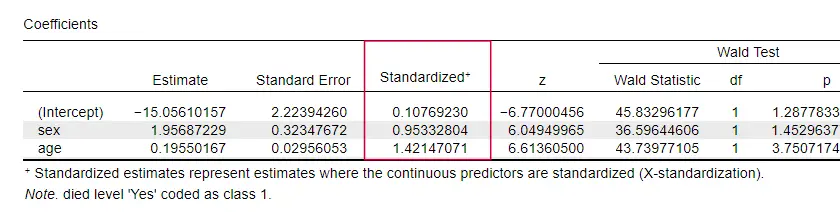
Hypothèses de régression logistique

L’analyse de régression logistique nécessite les hypothèses suivantes :

1. observations indépendantes ;
2. spécification correcte du modèle ;
3. mesure sans erreur de la variable de résultat et de tous les prédicteurs ;
4. linéarité : chaque prédicteur est lié linéairement à \(e^B\) (le rapport de cotes).

L’hypothèse 4 est quelque peu contestable et omise par de nombreux manuels1,6. Elle peut être évaluée avec le test de Box-Tidwell tel que discuté par Field4. Cela revient essentiellement à tester s’il y a des effets d’interaction entre chaque prédicteur et son logarithme naturel ou \(LN\).

Régression logistique multiple

Jusqu’ici, notre discussion s’est limitée à la régression logistique simple qui utilise un seul prédicteur. Le modèle est facilement étendu avec des prédicteurs supplémentaires, ce qui donne la régression logistique multiple :

$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,….+\,b_kX_{ki})}}$$

où

• \(P(Y_i)\) est la probabilité prédite que \(Y\) est vrai pour le cas \(i\);
• \(e\) est une constante mathématique d’environ 2.72;
• \(b_0\) est une constante estimée à partir des données;
• \(b_1\), \(b_2\), …. ,\(b_k\) sont les coefficients b pour les prédicteurs 1, 2, …. ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) sont les scores observés sur les prédicteurs \(X_1\), \(X_2\), … ,\(X_k\) pour le cas \(i\).

La régression logistique multiple implique souvent la sélection de modèles et la vérification de la multicollinéarité. À part cela, c’est une extension assez simple de la régression logistique simple.

Cette introduction de base était limitée aux éléments essentiels de la régression logistique. Si vous souhaitez en savoir plus, vous pouvez vous documenter sur certains des sujets que nous avons omis :

1. les rapports de cotes -calculés comme \(e^B\) dans la régression logistique- expriment la façon dont les probabilités changent en fonction des scores des prédicteurs ;
2. le test de Box-Tidwell examine si les relations entre les rapports de cotes susmentionnés et les scores des prédicteurs sont linéaires ;
3. le test de Hosmer et Lemeshow est un test alternatif de qualité d’ajustement pour un modèle de régression logistique entier.

Merci de lire!

1. Warner, R.M. (2013). La statistique appliquée (2e édition). Thousand Oaks, CA : SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistics. L’art &la science de l’apprentissage à partir des données. Essex : Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Analyse de données multivariées. New Jersey : Pearson Prentice Hall.
4. Field, A. (2013). Découvrir les statistiques avec IBM SPSS Statistics. Newbury Park, CA : Sage.
5. Howell, D.C. (2002). Méthodes statistiques pour la psychologie (5e éd.). Pacific Grove CA : Duxbury.
6. Pituch, K.A. &Stevens, J.P. (2016). Statistiques multivariées appliquées pour les sciences sociales (6e. édition). New York : Routledge.

.