• Ecuación de regresión logística
• Curvas de ejemplo de regresión logística
• Regresión logística – Coeficientes B
• Regresión logística – Tamaño del efecto
• Supuestos de la regresión logística

La regresión logística es una técnica para predecir una
variable de resultado dicotómica a partir de 1+ predictores.Ejemplo: ¿qué probabilidad tienen las personas de morir antes de 2020, dada su edad en 2015? Tenga en cuenta que «morir» es una variable dicotómica porque sólo tiene dos resultados posibles (sí o no).
Este análisis también se conoce como regresión logística binaria o simplemente «regresión logística». Una técnica relacionada es la regresión logística multinomial que predice variables de resultado con 3+ categorías.

Regresión logística – Ejemplo sencillo

Una residencia de ancianos tiene datos sobre el sexo de N = 284 clientes, la edad a 1 de enero de 2015 y si el cliente falleció antes del 1 de enero de 2020. Los datos en bruto se encuentran en esta hoja de Google, que se muestra parcialmente a continuación.

Centrémonos primero sólo en la edad:¿podemos predecir la muerte antes de 2020 a partir de la edad en 2015?Y -si es así- precisamente cómo? ¿Y en qué medida? Un buen primer paso es inspeccionar un gráfico de dispersión como el que se muestra a continuación.

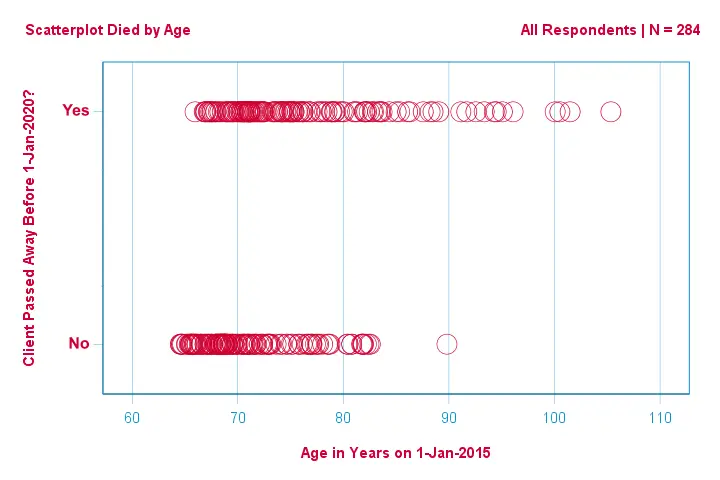
Algunas cosas que vemos en este gráfico de dispersión son que

• todos los clientes mayores de 83 años, excepto uno, murieron en los siguientes 5 años;
• la desviación estándar de la edad es mucho mayor para los clientes que murieron que para los que sobrevivieron;
• la edad tiene una asimetría positiva considerable, especialmente para los clientes que murieron.

¿Pero cómo podemos predecir si un cliente murió, dada su edad? Lo haremos ajustando una curva logística.

Ecuación de regresión logística simple

La regresión logística simple calcula la probabilidad de algún resultado dada una única variable de predicción como

$$P(Y_i) = \frac{1}{1 + e^{\},-\,(b_0\,+\,b_1X_{1i})}}$

donde

• (P(Y_i)\} es la probabilidad predicha de que \(Y\) sea verdadera para el caso \(i\);
• (e\) es una constante matemática de aproximadamente 2.72;
• (b_0\) es una constante estimada a partir de los datos;
• (b_1\) es un coeficiente b estimado a partir de los datos;
• (X_i\) es la puntuación observada en la variable \(X\) para el caso \(i\).

La esencia misma de la regresión logística es estimar \(b_0\) y \(b_1\). Estos dos números nos permiten calcular la probabilidad de que un cliente muera dada cualquier edad observada. Lo ilustraremos con algunas curvas de ejemplo que añadimos al gráfico de dispersión anterior.

Curvas de ejemplo de regresión logística

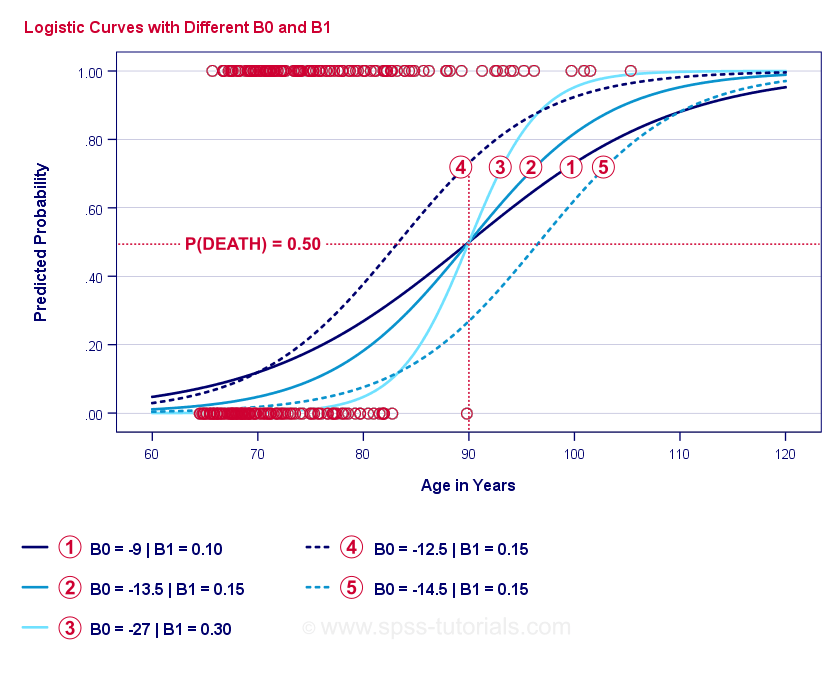
Si se toma un minuto para comparar estas curvas, puede ver lo siguiente:

• \(b_0\) determina la posición horizontal de las curvas: a medida que \(b_0\) aumenta, las curvas se desplazan hacia la izquierda, pero su inclinación no se ve afectada. Esto se observa en las curvas , y . Nótese que \(b_0\) es diferente pero \(b_1\) es igual para estas curvas.
• A medida que aumenta \(b_0\), las probabilidades predichas también aumentan: dada la edad = 90 años, la curva predice una probabilidad de morir de aproximadamente 0,75. Las curvas y predicen aproximadamente 0,50 y 0,25 probabilidades de morir para un cliente de 90 años.
• \(b_1\) determina la inclinación de las curvas: si \(b_1\) > 0, la probabilidad de morir aumenta con la edad. Esta relación se hace más fuerte a medida que \(b_1\) es mayor. Las curvas , y ilustran este punto: a medida que \(b_1\) se hace más grande, las curvas se hacen más pronunciadas por lo que la probabilidad de morir aumenta más rápido con el aumento de la edad.

Por ahora, nos queda una pregunta: ¿cómo encontramos el «mejor» \(b_0\) y \(b_1\)?

Regresión logística – Log Likelihood

Para cada encuestado, un modelo de regresión logística estima la probabilidad de que ocurra algún evento \(Y_i\). Evidentemente, estas probabilidades deben ser altas si el suceso ocurrió realmente y al revés. Una forma de resumir el rendimiento de un modelo para todos los encuestados es la probabilidad logarítmica (LL):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

donde

• \cdot(Y_i\) es 1 si el suceso ocurrió y 0 si no ocurrió;
• \cdot(ln\) denota el logaritmo natural: ¿a qué potencia hay que elevar \cdot(e\c) para obtener un número dado?

(LL\) es una medida de bondad de ajuste: en igualdad de condiciones, un modelo de regresión logística se ajusta mejor a los datos en la medida en que \(LL\) es mayor. De forma un tanto confusa, \(LL\) es siempre negativo. Por lo tanto, queremos encontrar el \(b_0\) y \(b_1\) para el cual
(LL\) es lo más cercano a cero como sea posible.

Estimación de Máxima Verosimilitud

En contraste con la regresión lineal, la regresión logística no puede calcular fácilmente los valores óptimos para \(b_0\) y \(b_1\). En su lugar, tenemos que probar diferentes números hasta que \(LL\) no aumente más. Cada intento de este tipo se conoce como una iteración. El proceso de encontrar los valores óptimos a través de tales iteraciones se conoce como estimación de máxima verosimilitud.

Así es como básicamente los programas estadísticos -como SPSS, Stata o SAS- obtienen los resultados de la regresión logística. Afortunadamente, son sorprendentemente buenos en ello. Pero en lugar de informar de \(LL\), estos paquetes informan de \(-2LL\). \(-2LL\) es una medida de «mal ajuste» que sigue una distribución
chi-cuadrado.Esto hace que \(-2LL\) sea útil para comparar diferentes modelos, como veremos en breve. \(-2LL\) se denota como -2 Log likelihood en la salida que se muestra a continuación.

La nota a pie de página aquí nos dice que la estimación de máxima verosimilitud necesitó sólo 5 iteraciones para encontrar los coeficientes b óptimos \(b_0\) y \(b_1\). Así que vamos a ver esos ahora.

Regresión Logística – Coeficientes B

La salida más importante para cualquier análisis de regresión logística son los coeficientes b. La figura siguiente los muestra para nuestros datos de ejemplo.

Antes de entrar en detalles, esta salida muestra brevemente

los coeficientes b que componen nuestro modelo;
los errores estándar de estos coeficientes b;
el estadístico Wald -calculado como \((\frac{B}{SE})^2\)- que sigue una distribución chi-cuadrado;
los grados de libertad para el estadístico Wald;
los niveles de significación para los coeficientes b;
los coeficientes b exponenciados o \(e^B\) son las odds ratios asociadas a los cambios en las puntuaciones de los predictores;
el intervalo de confianza del 95% para los coeficientes b exponenciados.

Los coeficientes b completan nuestro modelo de regresión logística, que ahora es

$$P(muerte_i) = \frac{1}{1 + e^{\},-\}(-9,079\},+\},0.124, \cdot\, edad_i)}}$$

Para un cliente de 75 años, la probabilidad de fallecer en un plazo de 5 años es

$P(muerte_i) = \frac{1}{1 + e^{,-\,(-9.079, +, 0,124, \cdot, 75)}=$

$P(muerte_i) = \frac{1}{1 + e^{, -, 0,249}=$

$P(muerte_i) = \frac{1}{1 + 0.780}=$$

$P(muerte_i) \aaproximadamente 0,562$

Así que ahora sabemos cómo predecir la muerte en 5 años dada la edad de alguien. ¿Pero cómo de buena es esta predicción? Hay varios enfoques. Empecemos con la comparación de modelos.

Regresión logística – Modelo de referencia

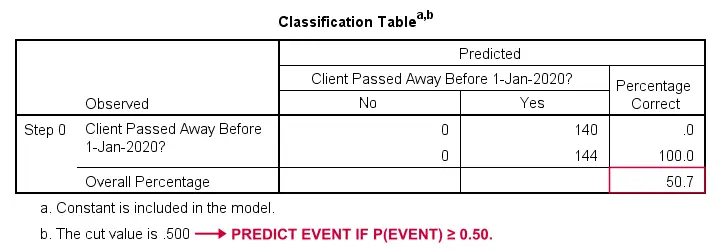
¿Cómo podríamos predecir quién falleció si no tuviéramos ninguna otra información? Bueno, el 50,7% de nuestra muestra falleció. Así que la probabilidad predicha sería simplemente 0,507 para todos.

Para fines de clasificación, solemos predecir que un evento ocurre si p(evento) ≥ 0,50. Como p(fallecido) = 0,507 para todos, simplemente predecimos que todos fallecieron. Esta predicción es correcta para el 50,7% de nuestra muestra que murió.

Regresión logística – Relación de verosimilitud

Ahora, a partir de estas probabilidades predichas y de los resultados observados, podemos calcular nuestra medida de mal ajuste: -2LL = 393,65. Nuestro modelo real -que predice la muerte por edad- da como resultado -2LL = 354,20. La diferencia entre estos números se conoce como ratio de probabilidad (LR):

$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Importantemente, \(LR\) sigue una distribución chi-cuadrado con \(df\) grados de libertad, calculado como

$$df = k_{model} – k_{baseline}$

donde \(k\) denota el número de parámetros estimados por los modelos. Como se muestra en esta Googlesheet, \(LR\) y \(df\) dan como resultado un nivel de significación para todo el modelo.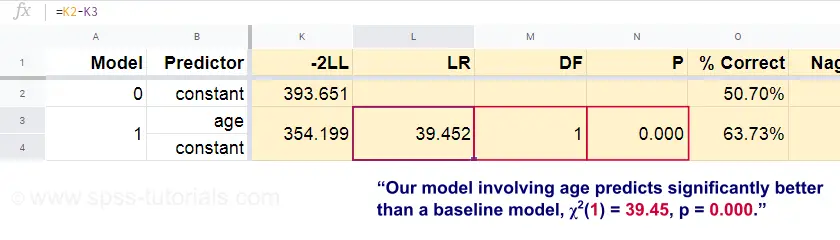

La hipótesis nula aquí es que algún modelo predice igual de mal que el modelo de referencia en alguna población. Dado que p = 0,000, rechazamos esto: nuestro modelo (que predice la muerte por edad) funciona significativamente mejor que un modelo de referencia sin ningún predictor.
¿Pero exactamente cuánto mejor? Esto se responde con su tamaño del efecto.

Regresión logística – Tamaño del efecto del modelo

Una buena manera de evaluar lo bien que funciona nuestro modelo es a partir de una medida del tamaño del efecto. Una opción es el Cox & Snell R2 o \(R^2_{CS}\) calculado como

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\\}(-2LL_{baseline})}{n}$

Lamentablemente, \(R^2_{CS}\}nunca alcanza su máximo teórico de 1. Por lo tanto, a menudo se prefiere una versión ajustada conocida como R2 de Nagelkerke o \(R^2_{N}):

$$R^2_{N} = \frac{R^2_{CS}{1 – e^{-\frac{-2LL_{baseline}}{n}$

Para los datos de nuestro ejemplo, \(R^2_{CS}} = 0,130, lo que indica un tamaño del efecto medio. \(R^2_{N}} = 0,173, un poco más grande que medio.

Por último, \(R^2_{CS}}) y \(R^2_{N}} son técnicamente diferentes de r-cuadrado como se calcula en la regresión lineal. Sin embargo, intentan cumplir la misma función. Por lo tanto, ambas medidas se conocen como medidas de pseudo r-cuadrado.

Regresión logística – Tamaño del efecto del predictor

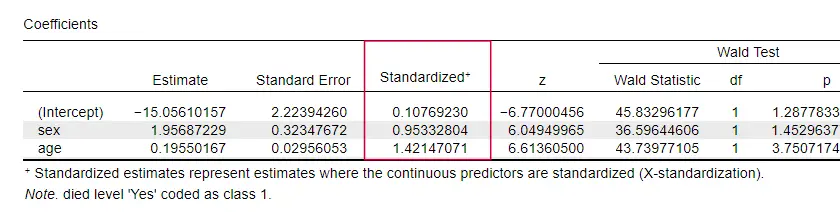
Extrañamente, muy pocos libros de texto mencionan cualquier tamaño del efecto para los predictores individuales. Tal vez sea porque éstos están completamente ausentes en SPSS. La razón por la que los necesitamos es que los coeficientes b dependen de las escalas (arbitrarias) de nuestros predictores: si introdujéramos la edad en días en lugar de en años, su coeficiente b se reduciría enormemente. Obviamente, esto hace que los coeficientes b sean inadecuados para comparar predictores dentro de un mismo modelo o entre diferentes modelos.
JASP incluye coeficientes b parcialmente estandarizados: los predictores cuantitativos -pero no la variable de resultado- se introducen como puntuaciones z, como se muestra a continuación.

Supuestos de la regresión logística

El análisis de la regresión logística requiere los siguientes supuestos:

1. observaciones independientes;
2. especificación correcta del modelo;
3. medición sin errores de la variable de resultado y de todos los predictores;
4. linealidad: cada predictor está relacionado linealmente con \(e^B\) (la razón de momios).

La hipótesis 4 es algo discutible y se omite en muchos libros de texto1,6. Puede evaluarse con la prueba de Box-Tidwell, tal como la discute Field4. Esto básicamente se reduce a probar si hay algún efecto de interacción entre cada predictor y su logaritmo natural o \ (LN\).

Regresión logística múltiple

Hasta ahora, nuestra discusión se ha limitado a la regresión logística simple que utiliza sólo un predictor. El modelo se amplía fácilmente con predictores adicionales, lo que da lugar a la regresión logística múltiple:

$$P(Y_i) = \frac{1}{1 + e^{\},(b_0,+\,b_1X_{1i}+,b_2X_{2}+,…+\\N,b_kX_{ki})}$$

donde

(P(Y_i)\N) es la probabilidad predicha de que \N(Y\N) sea cierta para el caso \N(i\N);
• (e\N) es una constante matemática de aproximadamente 2.72;
• (b_0\) es una constante estimada a partir de los datos;
• (b_1\), \(b_2\), … ,\(b_k\) son los coeficientes b de los predictores 1, 2, … |(k\\);
• (X_{1i}\), \(X_{2i}\), … \(X_{ki}) son las puntuaciones observadas en los predictores \(X_1\), \(X_2\), … ,\(X_k\) para el caso \(i\).

La regresión logística múltiple a menudo implica la selección del modelo y la comprobación de la multicolinealidad. Aparte de eso, es una extensión bastante sencilla de la regresión logística simple.

Esta introducción básica se limitó a lo esencial de la regresión logística. Si quiere aprender más, tal vez quiera leer algunos de los temas que hemos omitido:

1. las odds ratios -calculadas como \(e^B\) en la regresión logística- expresan cómo cambian las probabilidades en función de las puntuaciones de los predictores ;
2. la prueba de Box-Tidwell examina si las relaciones entre las odds ratios mencionadas y las puntuaciones de los predictores son lineales;
3. la prueba de Hosmer y Lemeshow es una prueba alternativa de bondad de ajuste para un modelo de regresión logística completo.

¡Gracias por leer!

1. Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Análisis de datos multivariantes. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statistical Methods for Psychology (5ª ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6ª. Edición). Nueva York: Routledge.