• Logistisk regression – ekvation
• Logistisk regression – exempel på kurvor
• Logistisk regression – B-koefficienter
• Logistisk regression – effektstorlek
• Logistisk regression Antaganden

Logistisk regression är en teknik för att förutsäga en
dichotom utfallsvariabel från 1+ prediktorer.Exempel: Hur sannolikt är det att människor kommer att dö före 2020, med tanke på deras ålder 2015? Observera att ”dö” är en dikotom variabel eftersom den endast har två möjliga utfall (ja eller nej).
Denna analys kallas också binär logistisk regression eller helt enkelt ”logistisk regression”. En besläktad teknik är multinomial logistisk regression som förutsäger utfallsvariabler med 3 eller fler kategorier.

Logistisk regression – enkelt exempel

Ett vårdhem har uppgifter om N = 284 klienters kön, ålder den 1 januari 2015 och huruvida klienten avled före den 1 januari 2020. Rådata finns i detta Googlesheet, som delvis visas nedan.

Låt oss först bara fokusera på åldern: kan vi förutsäga dödsfall före 2020 utifrån åldern 2015?Och i så fall exakt hur? Och i vilken utsträckning? Ett bra första steg är att inspektera ett spridningsdiagram som det som visas nedan.

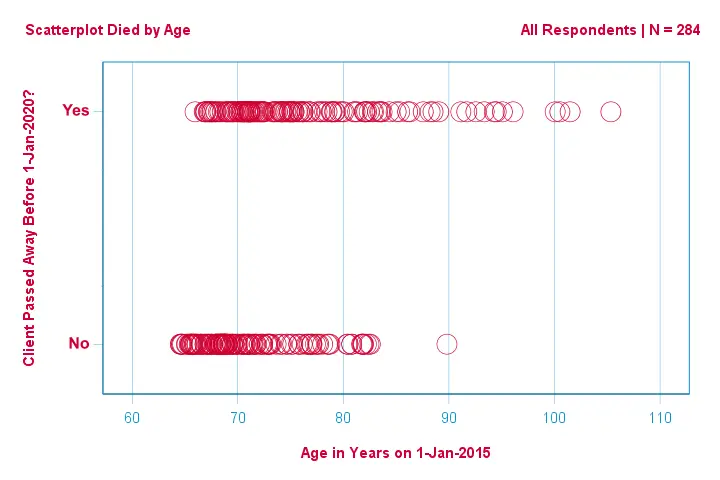Några saker vi ser i detta spridningsdiagram är att

• alla utom en klient över 83 år dog inom de kommande fem åren;
• standardavvikelsen för åldern är mycket större för klienter som dog än för klienter som överlevde;
• åldern har en avsevärd positiv skevhet, särskilt för de klienter som dog.

Men hur kan vi förutsäga om en klient har dött, med tanke på hans ålder? Vi gör just det genom att anpassa en logistisk kurva.

Enklare logistisk regressionsekvation

Enklare logistisk regression beräknar sannolikheten för ett visst utfall givet en enda prediktorvariabel som

$$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}$$$

där

• \(P(Y_i)\) är den förutsagda sannolikheten för att \(Y\) är sant för fallet \(i\);
• \(e\) är en matematisk konstant på ungefär 2.72;
• \(b_0\) är en konstant som uppskattas från data;
• \(b_1\) är en b-koefficient som uppskattas från data;
• \(X_i\) är den observerade poängen på variabeln \(X\) för fall \(i\).

Den logistiska regressionens själva kärna är att skatta \(b_0\) och \(b_1\). Dessa 2 tal gör det möjligt för oss att beräkna sannolikheten för att en klient ska dö med tanke på vilken observerad ålder som helst. Vi illustrerar detta med några exempelkurvor som vi lade till i det tidigare spridningsdiagrammet.

Exempelkurvor för logistisk regression

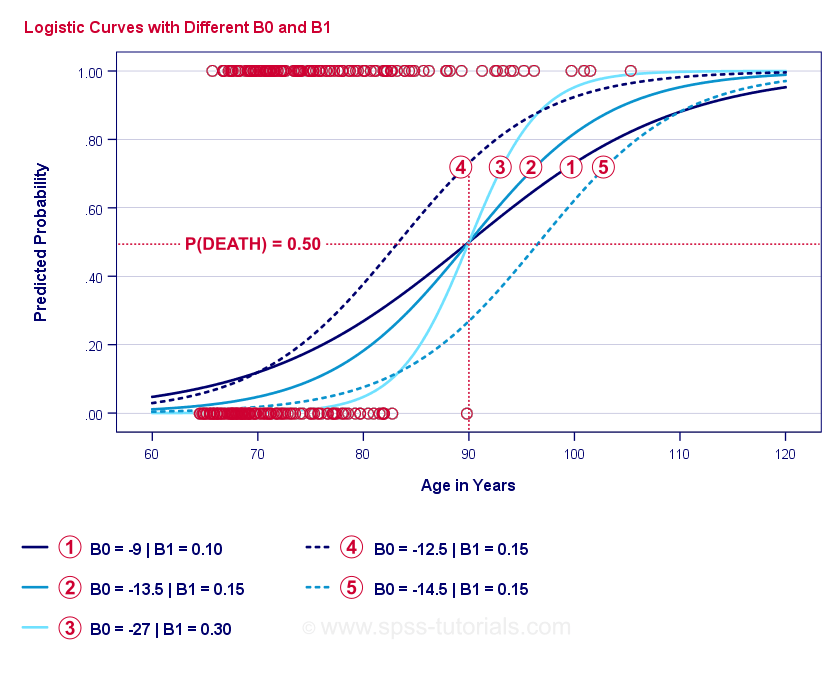
Om du tar dig en minut för att jämföra dessa kurvor kan du se följande:

• \(b_0\) bestämmer kurvernas horisontella läge: när \(b_0\) ökar förskjuts kurvorna åt vänster men deras branthet påverkas inte. Detta ses för kurvorna , och . Observera att \(b_0\) är olika men \(b_1\) är lika för dessa kurvor.
• Med ökande \(b_0\) ökar också de förutspådda sannolikheterna: givet ålder = 90 år förutspår kurva en sannolikhet på ungefär 0,75 att dö. Kurvorna och förutsäger ungefär 0,50 och 0,25 sannolikhet att dö för en 90-årig kund.
• \(b_1\) bestämmer kurvornas branthet: om \(b_1\) > 0, ökar sannolikheten att dö med stigande ålder. Detta förhållande blir starkare när \(b_1\) blir större. Kurvorna , och illustrerar detta: när \(b_1\) blir större blir kurvorna brantare så att sannolikheten att dö ökar snabbare med stigande ålder.

För nu har vi en fråga kvar: hur hittar vi de ”bästa” \(b_0\) och \(b_1\)?

Logistisk regression – log sannolikhet

För varje respondent uppskattar en logistisk regressionsmodell sannolikheten för att en viss händelse \(Y_i\) inträffade. Naturligtvis bör dessa sannolikheter vara höga om händelsen faktiskt inträffade och tvärtom. Ett sätt att sammanfatta hur väl en modell fungerar för alla respondenter är log-likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$$ där

• \(Y_i\) är 1 om händelsen inträffade och 0 om den inte inträffade;
• \(ln\) betecknar den naturliga logaritmen: med vilken potens måste man höja \(e\) för att få ett givet tal?

\(LL\\) är ett mått på god överensstämmelse: allt annat lika passar en logistisk regressionsmodell bättre in på data om \(LL\) är större. Något förvirrande är att \(LL\) alltid är negativ. Så vi vill hitta \(b_0\) och \(b_1\) för vilka
\(LL\) är så nära noll som möjligt.

Maximum Likelihood Estimation

I motsats till linjär regression kan logistisk regression inte utan vidare beräkna de optimala värdena för \(b_0\) och \(b_1\). Istället måste vi pröva olika tal tills \(LL\) inte ökar ytterligare. Varje sådant försök kallas för en iteration. Processen att hitta optimala värden genom sådana iterationer kallas maximum likelihood estimation.

Det är alltså i princip så statistiska program – såsom SPSS, Stata eller SAS – får fram logistiska regressionsresultat. Lyckligtvis är de otroligt bra på det. Men i stället för att rapportera \(LL\) rapporterar dessa paket \(-2LL\). \(-2LL\) är ett ”badness-of-fit”-mått som följer en
chi-square-fördelning. \(-2LL\) är därför användbart för att jämföra olika modeller, vilket vi kommer att se inom kort. \(-2LL\) betecknas som -2 Log likelihood i resultatet nedan.

Fotnoten här talar om att maximum likelihood-skattningen endast behövde 5 iterationer för att hitta de optimala b-koefficienterna \(b_0\) och \(b_1\). Så låt oss titta på dessa nu.

Logistisk regression – B-koefficienter

Det viktigaste resultatet för en logistisk regressionsanalys är b-koefficienterna. Figuren nedan visar dem för våra exempeldata.

För att gå in på detaljer visar denna utdata kortfattat

de b-koefficienter som ingår i vår modell;
standardfelen för dessa b-koefficienter;
Wald-statistiken -beräknad som \((\frac{B}{SE})^2\)- som följer en chi-kvadratfördelning;
frihetsgrader för Wald-statistiken;
signifikansnivåer för b-koefficienterna;
exponerade b-koefficienter eller \(e^B\) är de oddskvoter som är förknippade med förändringar i prediktorvärden;
95-procentigt konfidensintervall för de exponerade b-koefficienterna.

B-koefficienterna kompletterar vår logistiska regressionsmodell, som nu är

$$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9,079\,+\,0.124\, \cdot\, age_i)}}}$$$

För en 75-årig kund är sannolikheten att avlida inom 5 år

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}}=$$$

$$P(death_i) = \frac{1}{1 + e^{\,-\,0.249}}=$$$

$$P(death_i) = \frac{1}{1 + 0.780}=$$$

$$$P(death_i) \approx 0.562$$$

Så nu vet vi hur man kan förutsäga döden inom 5 år givet någons ålder. Men hur bra är denna förutsägelse? Det finns flera olika tillvägagångssätt. Låt oss börja med modelljämförelser.

Logistisk regression – grundmodell

Hur skulle vi kunna förutsäga vem som avled om vi inte hade någon annan information? Jo, 50,7 % av vårt urval avled. Så den förutspådda sannolikheten skulle helt enkelt vara 0,507 för alla.

För klassificeringssyften förutspår vi vanligtvis att en händelse inträffar om p(händelse) ≥ 0,50. Eftersom p(dog) = 0,507 för alla, förutsäger vi helt enkelt att alla har avlidit. Denna förutsägelse är korrekt för de 50,7 % av vårt urval som dog.

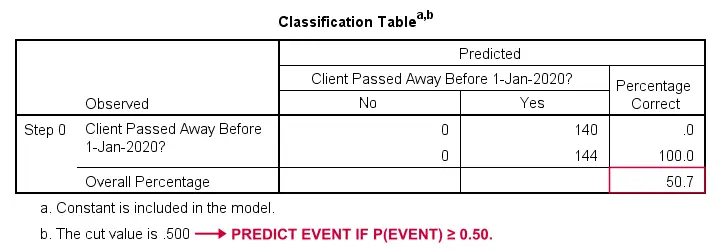
Logistisk regression – sannolikhetsförhållande

Nu kan vi från dessa förutsagda sannolikheter och de observerade utfallen beräkna vårt mått på dålig anpassning: -2LL = 393,65. Vår faktiska modell – som förutsäger död på grund av ålder – ger -2LL = 354,20. Skillnaden mellan dessa siffror kallas sannolikhetskvoten \(LR\):

$$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Väsentligt är att \(LR\) följer en chi-square-fördelning med \(df\) frihetsgrader, beräknad som

$$$df = k_{model} – k_{baseline}}$$$

där \(k\) anger antalet parametrar som uppskattas av modellerna. Som framgår av detta Googlesheet resulterar \(LR\) och \(df\) i en signifikansnivå för hela modellen.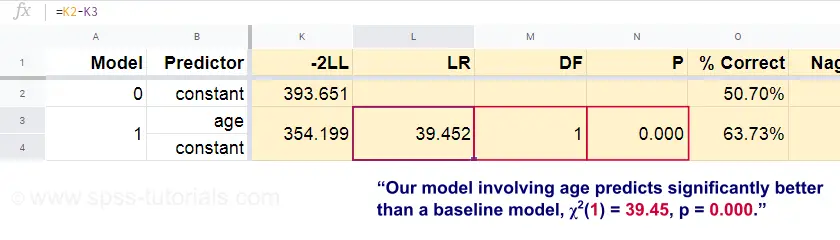

Nollhypotesen här är att någon modell förutsäger lika dåligt som grundmodellen i någon population. Eftersom p = 0,000 förkastar vi detta: vår modell (som förutsäger dödsfall på grund av ålder) presterar signifikant bättre än en grundmodell utan några prediktorer.
Men exakt hur mycket bättre? Detta besvaras av dess effektstorlek.

Logistisk regression – modellens effektstorlek

Ett bra sätt att utvärdera hur bra vår modell presterar är utifrån ett mått på effektstorlek. Ett alternativ är Cox & Snell R2 eller \(R^2_{CS}\) som beräknas som

$$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-\,(-2LL_{baseline})}{n}}$$$

Tråkigt nog når \(R^2_{CS}\) aldrig sin teoretiska maximala nivå på 1. Därför föredras ofta en justerad version som kallas Nagelkerke R2 eller \(R^2_{N}\):

$$$R^2_{N}} = \frac{R^2_{CS}}}{1 – e^{-\frac{-2LL_{baseline}}{n}}}$$

För våra exempeldata är \(R^2_{CS}\) = 0,130, vilket indikerar en medelstor effektstorlek. \(R^2_{N}\) = 0,173, vilket är något större än medium.

Sist \(R^2_{CS}\) och \(R^2_{N}\) är tekniskt sett helt annorlunda än r-kvadrat som beräknas vid linjär regression. De försöker dock fylla samma funktion. Båda måtten kallas därför pseudo r-kvadratmått.

Logistisk regression – prediktorernas effektstorlek

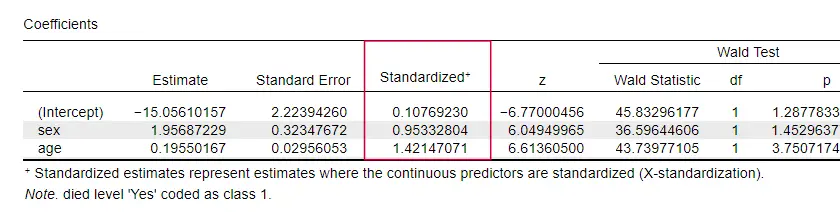
Oddartat nog är det mycket få läroböcker som nämner någon effektstorlek för enskilda prediktorer. Kanske beror det på att dessa är helt frånvarande i SPSS. Anledningen till att vi behöver dem är att b-koefficienter beror på (godtyckliga) skalor för våra prediktorer: om vi hade angett ålder i dagar i stället för år skulle dess b-koefficient krympa enormt. Detta gör naturligtvis b-koefficienter olämpliga för att jämföra prediktorer inom eller mellan olika modeller.
JASP innehåller delvis standardiserade b-koefficienter: kvantitativa prediktorer – men inte utfallsvariabeln – anges som z-poäng som visas nedan.

Antaganden för logistisk regression

Logistisk regressionsanalys kräver följande antaganden:

1. oberoende observationer;
2. korrekt modellspecifikation;
3. felfri mätning av utfallsvariabeln och alla prediktorer;
4. linjäritet: varje prediktor har ett linjärt samband med \(e^B\) (oddskvoten).

Förutsättning 4 är något omtvistad och utelämnas i många läroböcker1,6. Den kan utvärderas med Box-Tidwell-testet som diskuteras av Field4. Detta går i princip ut på att testa om det finns några interaktionseffekter mellan varje prediktor och dess naturliga logaritm eller \(LN\).

Multipel logistisk regression

Därför har vår diskussion hittills begränsats till enkel logistisk regression som endast använder en prediktor. Modellen kan lätt utökas med ytterligare prediktorer, vilket resulterar i multipel logistisk regression:

$$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,….+\,b_kX_{ki})}}}$$$

varvid

• \(P(Y_i)\) är den förutspådda sannolikheten för att \(Y\) är sant för fallet \(i\);
• (e\) är en matematisk konstant på ungefär 2.72;
• \(b_0\) är en konstant som uppskattas från data;
• \(b_1\), \(b_2\), … , \(b_k\) är b-koefficienten för prediktorerna 1, 2, …. ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) är observerade resultat för prediktorerna \(X_1\), \(X_2\), … ,\(X_k\) för fall \(i\).

Multipel logistisk regression innebär ofta modellval och kontroll av multikollinearitet. I övrigt är det en ganska okomplicerad utvidgning av enkel logistisk regression.

Denna grundläggande introduktion var begränsad till det väsentliga i logistisk regression. Om du vill lära dig mer kanske du vill läsa upp några av de ämnen som vi utelämnade:

1. Oddskvoter – som beräknas som \(e^B\) i logistisk regression – uttrycker hur sannolikheterna förändras beroende på prediktorpoäng;
2. Box-Tidwell-testet undersöker om sambanden mellan ovannämnda oddskvoter och prediktorpoäng är linjära;
3. Hosmer- och Lemeshow-testet är ett alternativt test för att bedöma om en hel logistisk regressionsmodell är välanpassad.

Tack för att du läste!

1. Warner, R.M. (2013). Tillämpad statistik (2:a upplagan). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariat dataanalys. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics (Upptäck statistik med IBM SPSS Statistics). Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.