För några månader sedan gick jag på ett kreativt origami-lunchmöte som anordnades av några underbara människor på $WORK. Jag hade gjort origami lite när jag var yngre, men mest bara grodor och tranor, som sedan dess har hjälpt mig att fördriva timmarna när jag övervakar tentor. Vid det här lunchtillfället fick jag dock lära mig hur man gör modulär origami. Detta innebär att man gör många (i allmänhet ganska enkla) origamidelar och sedan sätter ihop dem till större strukturer.

Jag gick hem med en enkel Sonobe-boll i 12 enheter den eftermiddagen och var mycket nöjd med mig själv.

Modulär origami på grundnivå: Sonobe-bollen i 12 enheter. Matematiskt sett är det en kumulerad oktaeder, praktiskt sett är det 12 ark kvadratiskt papper och ungefär en timme av din tid.
Det hela har eskalerat därifrån.

Mellan att jag själv driver några av dessa lunchsessioner nu, och att jag vid flera tillfällen har fått frågor på Twitter om hur jag gör de vackra sakerna som jag hela tiden twittrar om, tänkte jag att det skulle vara användbart att sammanställa en snabbguide (eller en länkfarm, i alla fall)..
Sonobe-enheter är mycket lätta att vika, ganska förlåtande, och kan användas för att göra en kub (6 enheter), en ackumulerad oktaeder (12 enheter), en ackumulerad isosaeder (30) och en slags avtrubbad isosaeder (90, i stort sett en taggig fotboll). De är en ganska bra introduktion till de allmänna principerna:

Sonobe-familjen: 90, 30, 12, 6 och 3 enheter. Den med 3 enheter är en trigonal bipyramid men räknas knappt! Dessa har alla tillverkats med den något modifierade enheten som nämns nedan. Den med 90 enheter är den största Sonobe som verkligen är värd att göra IMHO: ca 3 timmars arbete
Den med 30 enheter har symmetrierna hos en isosaeder (eller dodekaeder). När man väl har lärt sig hur man konstruerar det objektet i Sonobe-moduler har man i princip lärt sig hur man konstruerar vilken 30-modulig origamiboll som helst: det handlar oftast om att dela in 30 kantenheter i grupper om tre för att bilda de 12 femkantiga ytorna i en dodekaeder (eller motsvarande/alternativt att dela in dem i grupper om fem för att bilda de 20 triangulära ytorna i en isosaeder – skillnaden är mest en fråga om perspektiv).

Kumulerad icosaeder bestående av Sonobe-enheter: 30 pappersark och – om du har fått grepp om bollen med 12 enheter – fortfarande bara en timme av din tid
Det finns många variationer på Sonobe-enheten som du kan (åter)uppfinna, genom att lägga till bakåtvikningar som blottar den andra sidan av pappret, eller genom att göra flikarna smalare än fickorna, vilket ger ett mer intrikat utseende.

Kumulerad icosaeder gjord av något modifierade Sonobe-enheter
Och även om strukturen med 90 enheter är ganska stabil, tenderar nästa enhet (270 enheter) att hänga ihop under sin egen vikt med tiden, men vid det laget kändes det som en självklarhet att göra en sådan.

9 timmars byggande, plus lite planering. Här används duopapper, som är färgat på båda sidor, och en modifierad Sonobe-enhet som har ett omvänt veck för att exponera den andra sidan av pappret i varje modul.
Sonobe-enheterna kan också sättas ihop inifrån och ut för att göra inåtriktade polyeder…

Att få in de sista enheterna på den omvända bollen (till vänster) är knepigt.
…och de kan också sättas ihop i par och sedan sättas ihop till en spetsig pentakis-dodekaeder…

Pentakis dodekahedron, med en omvänd Sonobe-enhet som visar den andra sidan av pappret.
…och andra strukturer.

Sajten ovan beskriver detta som en rombisk triakontaedron, men jag är ganska säker på att det inte är det. Jag är dock inte säker på vad det faktiskt är. Har både färgbyte och enheterna är sammansatta ”inifrån och ut” för att göra den inåtriktad kumulativ.
Nästa enhet som jag provade var Penultimate edge unit (tillskriven Robert Neal), som kan användas för att göra en trådformad dodekaeder, vilket demonstreras av Matt Parker, stand-up-matematikern. Andra varianter av denna underenhet kan användas för att göra i stort sett vilken annan trådformad polyeder som helst.

Dodecahedron. Jag försökte använda det tråkiga färgade pappret på den här, men jag gillade resultatet i slutändan!
Thomas Hulls enhet PhiZZ edge gör liknande trådramsstrukturer, men modulerna passar bättre ihop och de resulterande strukturerna är mycket mer robusta än vad man får med de näst sista modulerna.

Truncated icosahedron – detta är i princip formen på en fotboll (12 femhörningar, omgivna av sexhörningar) och på vissa viruskapsider också.
Du kan också göra varianter med färgbyte med hjälp av den teknik som visas i Lewis Simons dekorationslådor.

Dodekaeder tillverkad av PHiZZ-enheter med färgbyte.
För strukturer baserade på dodekaeder/icosaeder och tillverkade av kant-enheter kan man alltid komma undan med att bara använda tre färger och aldrig ha två stycken av samma färg som rör varandra. Detta beror på att man kan rita en Hamiltons krets på en dodekaeder: det är en väg från hörn till hörn som bara besöker varje hörn en gång, och som kommer tillbaka till där den började. Du kan representera detta i 2D på ett Schlegeldiagram.
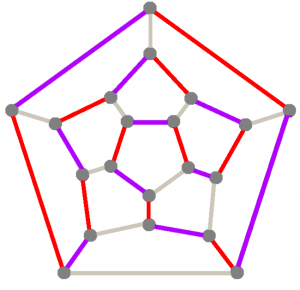
Hamiltonsk krets genom Schlegeldiagrammet av en dodekaeder . De röda och lila kanterna bildar den hamiltoniska kretsen; de grå kanterna är det som är kvar. Du kommer att märka att varje hörn har en av var och en av de tre färgade kanterna. Diagrammet är en projektion av en dodekaeder: tänk dig att du tar en trådmodell av dodekaedern och lyser med en ficklampa genom den: Schlegeldiagrammet är den 2D-skugga som denna 3D-polyeder kastar på väggen. Det är ganska enkelt att räkna ut vilken kant i 2D-diagrammet som motsvarar vilken kant i det du bygger.
Om du färgar alternerande kanter i Hamiltons krets i två av dina valda färger, och resten av kanterna i den tredje, så undviker du att få färgkollisioner. Jag lärde mig detta först efter att jag började göra dessa strukturer, så alla har inte denna optimala färgning! Samma 3-färgsregel gäller för de andra platonska soliderna, och även för den trunkerade ikosaedern.
Francesco Mancinis star-holes kusudama använder en liknande modul som PHiZZ, men med en liten bakåtböjning som ger en snygg 3D-stjärnverkan. Den här är dodekaederformad (30 enheter), men en trunkerad icosaeder med 90 enheter borde också vara möjlig.

Stjärnhål dodekaeder.
UPPDATERING: ja, det är möjligt 🙂

Star-holes truncated icosahedron
Lewis Simon och Bennett Arnsteins triangelns kantenhet kan användas för att göra mycket fina patchtwork-tetraeder, oktaeder och icosaeder.

Icosahedron.
De är lite krångliga att sätta ihop men är mycket robusta när de väl är konstruerade. En liknande lappverkseffekt för dodekaedern kan åstadkommas med M. Mukhopadhyays paraplymodul; Sonobe-enheter kan användas för att göra analoga kuber i stil med Battenbergkakor.

Battenberg-kake platoniska solider. Dodekaedern tillverkas av paraplyenheter, kuben av Sonobe. Tetraedern, oktaedern och isosaedern är alla gjorda av triangelkantmoduler.
Den enkla isoccelesiska triangelenheten (som på olika sätt tillskrivs M. Mukhopadhyay, Jeannine Mosely och Roberto Morassi) kan användas för att göra små och stora stjärnformade dodekaedrar.

Stora (till vänster) och små (till höger) stjärnformade dodokaedrar.
Den lilla stjärnformade dodokaedern är särskilt tilltalande och utgör en ganska robust dekoration om den tillverkas av folierat papper.

Juldekor
Den stora stellated dodekaedern kan tillverkas av samma underenhet, men är knepigare att konstruera eftersom en flik måste ringla runt till en ficka som delvis ligger inuti nästa flikrunda. Jag använde en nåltång för att konstruera denna, och jag är fortfarande inte särskilt nöjd med resultatet.
Det motsatta gäller för Paolo Bascettas stjärnmodul, som gör en stor stor stellated dodekahedron, men en ganska *eh* liten stellation. Denna modul behöver duopapper (dvs. papper som är färgat på båda sidor) för bästa effekt.

Stor (vänster) och liten (höger) stellated dodekahedra.
Dave Mitchells Electra-modul kan användas för att göra en icosidodekahedron: den är ovanlig i det avseendet att varje modul motsvarar en hörnpunkt i strukturen: de kantenheter som beskrivits hittills kombineras tillsammans för att skapa varje hörnpunkt.

Icosidodekaeder gjord av Electra-moduler
Jag är inte så nöjd med min Void kusudama (Tadashi Mori): Jag borde ha använt duopapper, men det var verkligen knepigt att sätta ihop den. Kanske en dag. Det är en av de få strukturer här som är tillbaka till den ursprungliga oktaedriska/kubiska 12-enhetsstrukturen. Jag är inte säker på att 30-enhetsversionen skulle vara stabil.

Octaedral void
UPPDATERING: Ja, jag tror inte att versionen med 30 enheter är genomförbar. Jag tror att enheterna är för breda för att faktiskt passa in i en icosaeder: Jag kunde inte ens klara det med lim, så jag tror inte att det bara är ett stabilitetsproblem. Jag gjorde dock en bättre version med 12 enheter, med duopapper och ett litet omvänt veck på ytterkanten för att exponera den andra färgen ordentligt, som jag är ganska nöjd med:

Octahedral void (modified)
Tomoko Fusés små sköldpaddsmoduler är extremt flexibla: de kan användas för att göra i stort sett vilken polyeder som helst som består av regelbundna polygoner. Eftersom klapparna bara är ett papperslager tjocka passar de dock inte ihop fruktansvärt tätt, så jag har bara funnit dem tillräckligt robusta för att göra mindre strukturer utan hjälp av lim. Med hjälp av lim har jag dock gjort en rombikosidodekaeder, som är häftig eftersom den är uppbyggd av femhörningar, trianglar och kvadrater (alla polygoner som finns i de platonska soliderna)…

Den omöjliga rombikosidodekaedern att stava till.
…och även ett par snub-kuber, som är ännu mer intressanta eftersom snub-kuben har två icke-superimponerbara spegelbilder, som händer, aminosyror och amfetamin.

Snubcubes: vänster- och högerhänta enatiomorfer.
Jag hittade Maria Sinayskaya Etna kusudama i Meenakshi Mukerjis bok Exquisite Modular Origami. Det är en riktigt vacker modell, och robust när den väl är monterad, men den kan vara lite fally-aparty under byggandet: Jag använde mycket små klädnypor för att hålla ihop den när jag gjorde den.

Etna kusudama.
Meenakshi Mukerjis sammansättning av fem oktaeder (inspirerad av Dennis Walker) är också lite fally-aparty, men jag gillar den eftersom den – till skillnad från många av dessa modeller – verkligen är en polyeder med samma namn, snarare än något där man måste blinka på hålen i stålramen och föreställa sig ansikten där.

Sammansättning av fem oktaeder. Du kan lätt se den gula oktaedern här: den sjätte spiken är under modellen; de andra fyra färgerna är på liknande sätt sammanflätade.
De fem korsande tetraederna är faktiskt mycket lättare att göra än de ser ut. Francis Ows 6 graders moduler i sig är lätta att vika, och topparna är mycket mer robusta än de kan verka. Det svåraste är att få modulerna sammanlänkade på rätt sätt. Jag har lyckats två gånger, men bara medan jag stirrade på YouTube-videon och utförde diverse ”lila = grön” gymnastik i mitt huvud.

Sammansättning av fem tetraedrar – party piece.
Michał Kosmulskis sida har många fina illustrationer, instruktioner och inspiration. Jag hittade Tung Ken Lams blintz icosadodekahedron (även krediterad som Francesco Mancinis UVWXYZ intersecting planes model) där. Den har samma symmetri som Electra-ikosadodekaedern ovan, men man kan se de sex korsande femkanterna tydligare. Båda har samma underliggande struktur som Hoberman-sfären – den där expanderande/kontraherande plastpinne-modellen som är älskad på vetenskapsmässor.

UVWXYZ skärande plan icosadodekaeder
Detta sista är lite av ett fusk eftersom (i teorin, och för det mesta också i praktiken) strukturerna ovan inte hålls samman av något annat än friktion. Valentina Gonchars avslöjade flower star kusudama måste limmas, vilket är lite fusk, men jag kunde inte låta bli eftersom det är två strukturer i en:

Revealed flower star – closed (left) and popped open (right).
Saker som jag fortfarande skulle vilja göra:
- Bygg en mycket större PhiZZ-boll (270 enheter): detta skulle vara användbart för att demonstrera strukturerna hos viruskapsider. UPDATE: Klart!

För…

…Efter
- Jag har ännu inte hittat någon bra modell av en stor dodekaedermodell: de finns på Pintrest, men jag har ännu inte hittat några instruktioner för en. UPDATE: Klart! (Kunde inte för mitt liv räkna ut hur man gör 3-färgning, men modulen är från Saku B, rekommenderad av Nick i kommentarerna nedan)

Great dodecahedron
- Jag har tappat bort var det nu var jag hittade instruktionerna för denna inåt kumulativa rombiska triacontahedron: Jag skulle gärna vilja återupptäcka dem så att jag kan skriva under på uppfinnaren! UPDATE: Det var inte här jag ursprungligen såg den, men AresMares by Gewre har en videohandledning, och en vänlig kommentator har låtit mig veta att konstruktören är Silvana Betti Mamino – tack!

Rombisk triacontahedron av okänd källa.
- Uppfinna min egen modul 🙂