Radioaktív bomlási törvény
Amikor egy egyedi atommag sugárzás kibocsátásával egy másik atommaggá alakul át, azt mondjuk, hogy az atommag bomlik. A radioaktív bomlás minden \(Z > 82\) atommag esetében, valamint néhány \(Z < 83\) instabil izotóp esetében is bekövetkezik. A bomlási sebesség arányos az anyagban lévő eredeti (nem bomlott) atommagok N számával. A bomlással elveszett atommagok számát, \(-dN\) dt időintervallumban,
\
írjuk fel, ahol \(\lambda\) a bomlási állandó. (A mínusz jel azt jelzi, hogy az eredeti atommagok száma az idő múlásával csökken.) Más szóval, minél több atommag áll rendelkezésre a bomláshoz, annál több bomlik el (dt idő alatt). Az \ref{eq2} egyenlet átírható a következőképpen:
\
Az egyenlet mindkét oldalát integráljuk, és \(N_0\) az \(t = 0\) időpontban lévő atommagok száma, megkapjuk
\
Az egyenlet bal és jobb oldalát \ref{eq4} \(e\) hatványaként véve, megkapjuk a radioaktív bomlási törvényt.
Radioaktív bomlási törvény
Az \(t\) idő után megmaradó radioaktív atommagok teljes száma \(N\)
\
ahol \(\lambda\) az adott atommag bomlási állandója.
A magok teljes száma először nagyon gyorsan, majd lassabban csökken (\(\PageIndex{2}\) ábra).
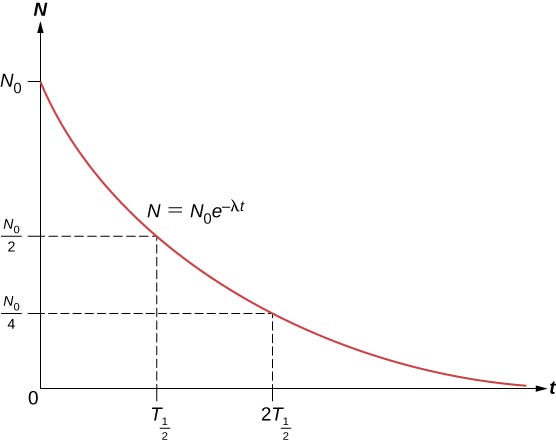
A radioaktív anyag \((T_{1/2})\) felezési ideje az az idő, amíg az eredeti atommagok fele bomlik (vagy az az idő, amikor az eredeti atommagok fele marad). Az instabil izotópok felezési idejét a nuklidok táblázata mutatja. Az egész számú (n) felezési idő után megmaradó radioaktív atommagok száma tehát
\
Ha a bomlási állandó \((\lambda)\) nagy, a felezési idő kicsi, és fordítva. E mennyiségek közötti kapcsolat meghatározásához vegyük észre, hogy ha \(t = T_{1/2}\), akkor \(N = N_0/2\).
Ezért az \ref{eq5} egyenlet átírható
\
Mindkét oldalt \(N_0\)-vel osztva és a természetes logaritmust véve megkapjuk
\
, ami
\
re csökken, ha ismerjük egy radioaktív anyag T1/2 felezési idejét, meg tudjuk találni a bomlási állandóját. Egy radioaktív anyag \(\overline{T}\) élettartamát úgy határozzuk meg, mint azt az átlagos időtartamot, amely alatt egy atommag bomlás előtt létezik. Az anyag élettartama nem más, mint a bomlási állandó reciproka, amit így írunk fel:
\\
Az A aktivitást a bomlási sebesség nagyságaként határozzuk meg, vagy
\
A dt időintervallumban bekövetkező dN végtelenül kicsi változás negatív, mert az anyarészecskék (nem bomlott) száma csökken, így az aktivitás (A) pozitív. Ha a kezdeti aktivitást \(A_0 = \lambda N_0\)-ként határozzuk meg, akkor
\
A radioaktív anyag A aktivitása tehát exponenciálisan csökken az idővel (\(\PageIndex{3}\) ábra).
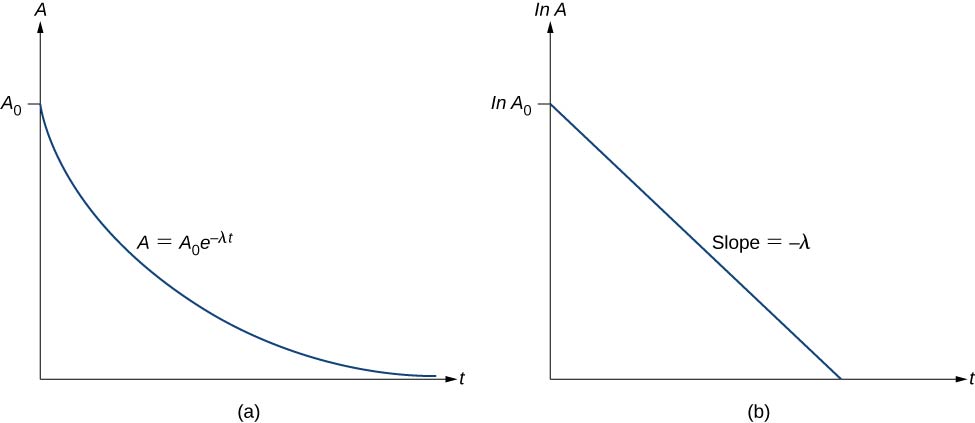
Példa \(\PageIndex{1}\): A stroncium-90 felezési ideje \(\ce{_{38}^{90}Sr}\) 28,8 y. Keressük meg (a) a bomlási állandóját és (b) 1,00 g anyag kezdeti aktivitását.
Stratégia
A bomlási állandót közvetlenül az \ref{eq8} egyenletből találhatjuk meg. Az aktivitás meghatározásához először meg kell találnunk a jelen lévő atommagok számát.
Megoldás
a. Megállapítjuk, hogy a bomlási állandó
\
b. A \(_{38}^{90}Sr\) atomtömege 89,91 g. Az Avogadro-szám \(N_A = 6,022 \szer 10^{23}\) atom/mol segítségével megtaláljuk az 1,00 g anyagban lévő atommagok kezdeti számát:
\
Ebből megállapíthatjuk, hogy az aktivitás \(A_0\) \(t = 0\) esetén 1 \(t = 0\).00 g stroncium-90 esetében
\
Az \(\lambda\) értékét az anyag felezési idejével kifejezve megkapjuk
\
Az aktivitás tehát egy felezési idő után a felére csökken. Az \(\lambda\) bomlási állandóját az aktivitás idő függvényében történő mérésével határozhatjuk meg. Az \ref{eq11} egyenlet bal és jobb oldalának természetes logaritmusát véve megkapjuk
\
Ez az egyenlet a lineáris \(y = mx + b\) formát követi. Ha \ln A-t ábrázoljuk t függvényében, egyenes egyenest várunk, amelynek meredeksége \(-\lambda\) és y-interceptusa \(\ln \, A_0\) (\(\(\PageIndex{3b}\) ábra). Az A aktivitást becquerel (Bq) egységben fejezzük ki, ahol egy \(1 \, Bq = 1 \, bomlás \, per \, másodperc\). Ez a mennyiség percenkénti bomlásokban vagy évenkénti bomlásokban is kifejezhető. Az aktivitás egyik legelterjedtebb mértékegysége a curie (Ci), amelyet 1 g \(^{226}Ra\) aktivitásaként határoznak meg. A Bq és a Ci közötti kapcsolat
\
Példa \(\PageIndex{2}\):
Az emberi test tömegének körülbelül \(20\%\) része szén. Számítsa ki az \(^{14}C\) aktivitását 1,00 kg élő szervezetben található szénben. Fejezze ki az aktivitást Bq és Ci egységekben.
Stratégia
Az \(^{14}C\) aktivitását a \(A_0 = \lambda N_0\) egyenlet segítségével határozzuk meg, ahol λ a bomlási állandó és \(N_0\) a radioaktív atommagok száma. Az 1,00 kg-os mintában lévő \(^{14}C\) atommagok számát két lépésben határozzuk meg. Először meghatározzuk az \(^{12}C\) atommagok számát a mól fogalmának segítségével. Másodszor megszorozzuk ezt az értéket \(1,3 \szor 10^{12}\) (az \(^{14}C\) ismert gyakorisága egy élő szervezetből származó szénmintában), hogy meghatározzuk az \(^{14}C\) atommagok számát egy élő szervezetben. A bomlási állandót az \(^{14}C\) ismert felezési idejéből határozzuk meg (elérhető a ).
Solution
Egy mol szén tömege 12,0 g, mivel közel tiszta \(^{12}C\). Így a szén atommagok száma egy kilogrammban
\
Az \(^{14}C\) atommagok száma 1 kg szénben tehát
\
Most az \ref{eq11} egyenlet segítségével meg tudjuk találni az \(A\) aktivitást. Ismert értékek megadásával megkapjuk
\
vagy \(7,89 \szer 10^9\) bomlást évente. Ahhoz, hogy ezt átkonvertáljuk a Bq egységre, egyszerűen alakítsuk át az éveket másodpercekre. Így
\
vagy 250 bomlás másodpercenként. Ahhoz, hogy A-t curie-ben fejezzük ki, használjuk a curie definícióját,
\
Így,
\
jelentősége
Az emberi test tömegének körülbelül \(20\%\) része szén. Az emberi szervezetben másodpercenként több száz \(^{14}C\) bomlás megy végbe. A szén-14 és más, a szervezetben természetesen előforduló radioaktív anyagok alkotják az ember nukleáris sugárzásnak való háttérkitettségét. Amint azt a fejezet későbbi részében látni fogjuk, ez az aktivitási szint jóval a maximálisan ajánlott dózisok alatt van.