Bevezetés

A döntési fa egyfajta felügyelt tanulási algoritmus, amely egyaránt használható regressziós és osztályozási problémákra. Kategorikus és folytonos bemeneti és kimeneti változók esetén egyaránt működik.

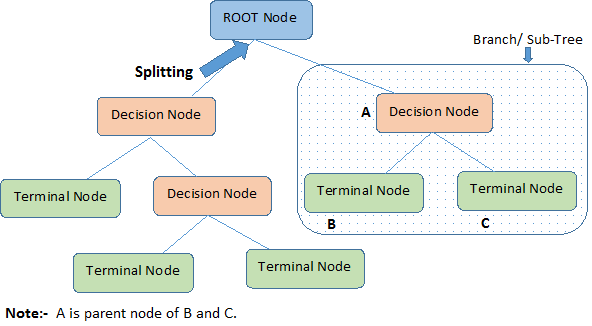
A fenti képet nézve azonosítsuk a döntési fával kapcsolatos fontos fogalmakat:

• A gyökércsomópont a teljes populációt vagy mintát képviseli. Ez a továbbiakban két vagy több homogén halmazra oszlik.

• A felosztás egy csomópont két vagy több alcsomópontra történő felosztása.

• Amikor egy alcsomópont további alcsomópontokra oszlik, azt döntési csomópontnak nevezzük.

• Azokat a csomópontokat, amelyek nem osztódnak szét, végcsomópontnak vagy levélnek nevezzük.

• Ha egy döntési csomópont alcsomópontjait eltávolítjuk, ezt a folyamatot metszésnek nevezzük. A metszés ellentéte a Felosztás.

• A teljes fa egy alrészletét ágnak nevezzük.

• Az alcsomópontokra osztott csomópontot az alcsomópontok szülőcsomópontjának nevezzük; míg az alcsomópontokat a szülőcsomópont gyermekének.

A döntési fák típusai

Regressziós fák

Nézzük meg az alábbi képet, amely segít szemléltetni a regressziós fa által végzett felosztás jellegét. Ez egy metszetlen fát és egy véletlenszerű adathalmazra illesztett regressziós fát mutat. Mindkét ábrázolás a fa tetején kezdődő felosztási szabályok sorozatát mutatja. Vegyük észre, hogy a tartomány minden felosztása az egyik jellemzőtengelyhez igazodik. A tengellyel párhuzamos felosztás koncepciója egyszerűen általánosítható kettőnél nagyobb dimenziókra. Egy $p$ méretű jellemzőtér esetében, amely a $\mathbb{R}^p$ részhalmaza, a teret $M$ régióra, $R_{m}$-ra osztjuk, amelyek mindegyike egy $p$ dimenziós “hiperblokk”.

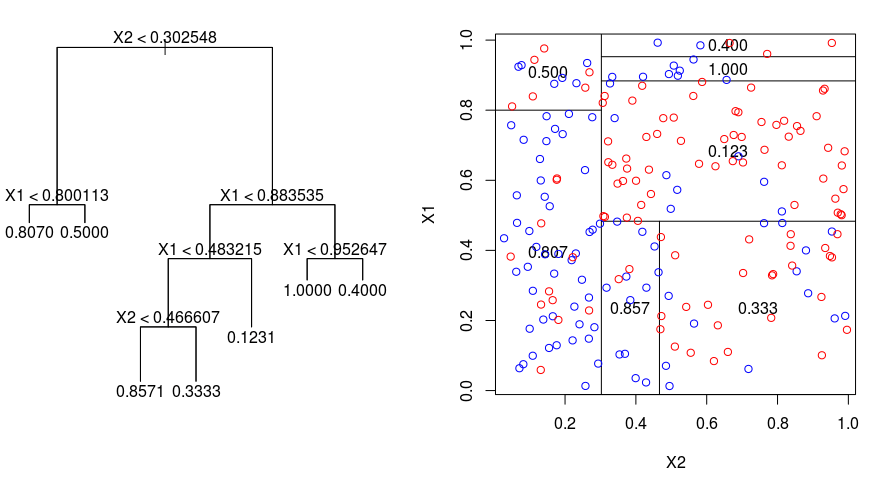
A regressziós fa felépítéséhez először rekurzív bináris osztás segítségével egy nagy fát növesztünk a képzési adatokon, és csak akkor állunk meg, ha minden végponton kevesebb megfigyelés van, mint bizonyos minimális számú. A rekurzív bináris osztás egy mohó és felülről lefelé irányuló algoritmus, amelyet a lineáris regressziós beállításokban is használt hibamérték, a maradék négyzetek összegének (RSS) minimalizálására használnak. Az RSS egy M partícióval rendelkező partícionált jellemzőtér esetén a következőképpen adódik:

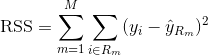
A fa tetejéről kiindulva 2 ágra osztjuk, 2 tér partícióját létrehozva. Ezután ezt az adott felosztást a fa tetején többször is elvégezzük, és kiválasztjuk a jellemzőknek azt a felosztását, amelyik minimalizálja az (aktuális) RSS-t.

A következőkben a nagy fára költségbonyolultsági metszést alkalmazunk, hogy a $\alpha$ függvényében megkapjuk a legjobb részfák sorozatát. Az alapötlet itt az, hogy bevezetünk egy további, $\alpha$-val jelölt hangolási paramétert, amely kiegyensúlyozza a fa mélységét és a képzési adatokhoz való illeszkedésének jóságát.

A $\alpha$ kiválasztásához használhatunk K-szoros keresztvalidálást. Ez a technika egyszerűen azt jelenti, hogy a képzési megfigyeléseket K hajtogatásra osztjuk, hogy megbecsüljük a részfák tesztelési hibaarányát. A cél az, hogy kiválassza azt, amelyik a legkisebb hibaarányhoz vezet.

Klasszifikációs fák

Az osztályozási fa nagyon hasonlít a regressziós fához, azzal a különbséggel, hogy nem mennyiségi, hanem minőségi válasz előrejelzésére szolgál.

Memlékezzünk arra, hogy egy regressziós fa esetében egy megfigyelésre adott előrejelzett választ az azonos végcsomóponthoz tartozó képzési megfigyelések átlagos válasza adja. Ezzel szemben egy osztályozási fa esetében azt jósoljuk meg, hogy minden megfigyelés a gyakorló megfigyelések azon régiójában leggyakrabban előforduló osztályba tartozik, amelyhez tartozik.

Az osztályozási fa eredményeinek értelmezésekor gyakran nemcsak az adott végcsomópont régiójának megfelelő osztályjóslás érdekli, hanem az adott régióba tartozó gyakorló megfigyelések közötti osztályarányok is.

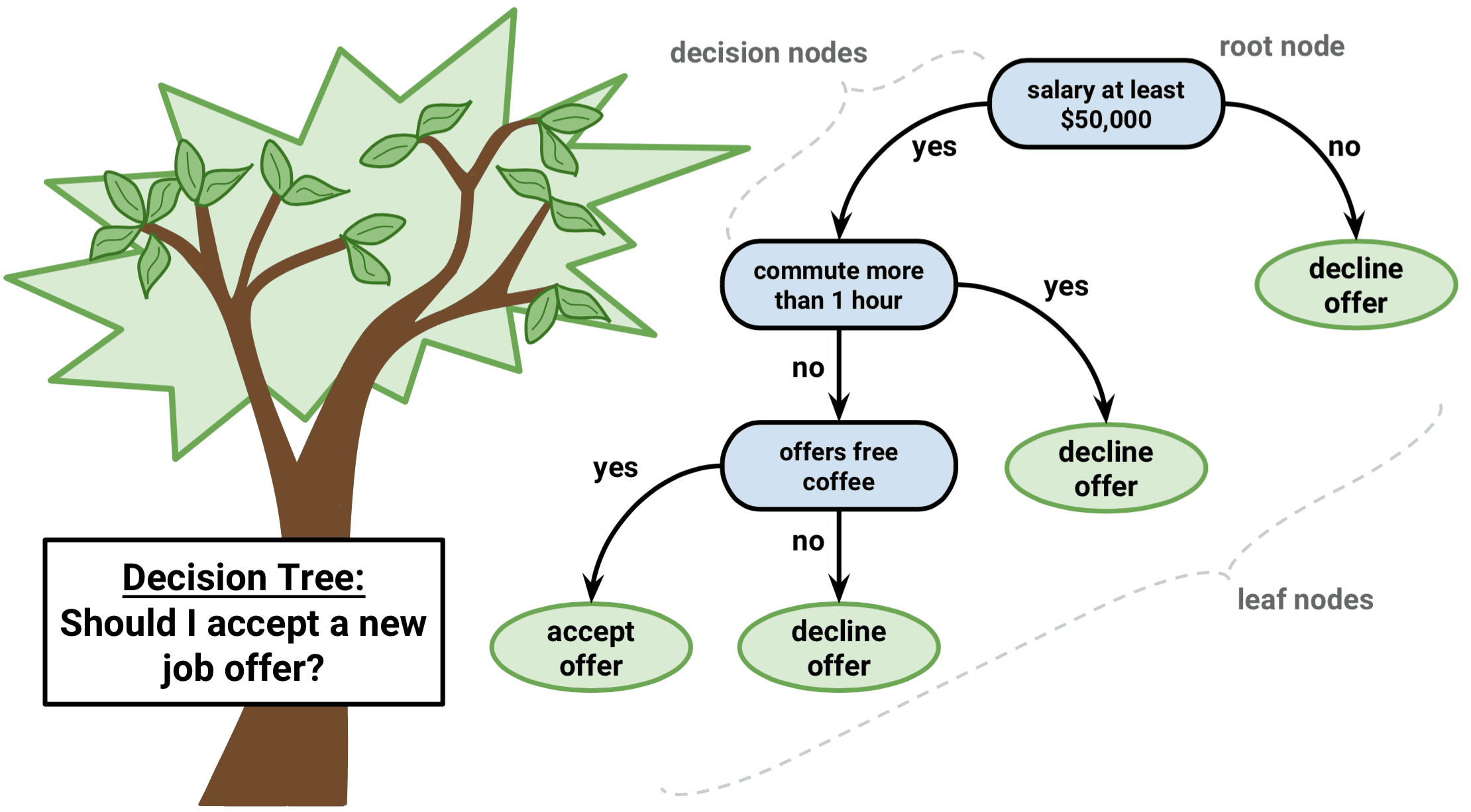
Az osztályozási fa növesztésének feladata nagyon hasonló a regressziós fa növesztésének feladatához. Csakúgy, mint a regressziós környezetben, rekurzív bináris felosztást használunk az osztályozási fa növesztéséhez. Az osztályozási beállításban azonban a négyzetek reziduális összege nem használható kritériumként a bináris osztások elkészítéséhez. Ehelyett az alábbi 3 módszer valamelyikét használhatja:

• Osztályozási hibaarány: Ahelyett, hogy azt nézné, hogy egy numerikus válasz milyen messze van az átlagértéktől, mint a regressziós beállításban, ehelyett a “találati arányt” úgy határozhatja meg, mint a képzési megfigyelések azon hányadát egy adott régióban, amelyek nem tartoznak a leggyakrabban előforduló osztályba. A hibát ez az egyenlet adja meg:

E = 1 – argmaxc($\hat{\pi}_{mc}$)

melyben $\hat{\pi}_{mc}$ az Rm régióban található képzési adatok azon hányadát jelenti, amelyek a c osztályba tartoznak.

• Gini-index: A Gini-index egy alternatív hibamérő, amelynek célja, hogy megmutassa, mennyire “tiszta” egy régió. A “tisztaság” ebben az esetben azt jelenti, hogy egy adott régióban a képzési adatok mekkora része tartozik egyetlen osztályba. Ha egy Rm régió olyan adatokat tartalmaz, amelyek nagyrészt egyetlen c osztályból származnak, akkor a Gini-index értéke kicsi lesz:

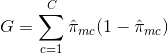
• Kereszt-entrópia: Egy harmadik, a Gini-indexhez hasonló alternatívát kereszt-entrópiának vagy devianciának nevezzük:

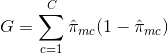
A kereszt-entrópia akkor vesz fel nullához közeli értéket, ha a $\hat{\pi}_{mc}$ értékei mind 0 vagy 1 közelében vannak. Ezért a Gini-indexhez hasonlóan a kereszt-entrópia is kis értéket vesz fel, ha az m-edik csomópont tiszta. Valójában kiderül, hogy a Gini-index és a kereszt-entrópia numerikusan nagyon hasonló.

Az osztályozási fa építése során általában a Gini-indexet vagy a kereszt-entrópiát használják egy adott felosztás minőségének értékelésére, mivel ezek érzékenyebbek a csomópontok tisztaságára, mint az osztályozási hibaarány. E 3 megközelítés bármelyike használható a fa metszésekor, de az osztályozási hibaarány előnyösebb, ha a végső metszett fa előrejelzési pontossága a cél.

A döntési fák előnyei és hátrányai

A döntési fák használatának legfőbb előnye, hogy intuitív módon nagyon könnyen magyarázhatóak. Más regressziós és osztályozási megközelítésekkel összehasonlítva nagyon jól tükrözik az emberi döntéshozatalt. Grafikusan megjeleníthetők, és könnyen kezelik a kvalitatív prediktorokat anélkül, hogy dummy változókat kellene létrehozni.

A döntési fák azonban általában nem rendelkeznek olyan szintű előrejelzési pontossággal, mint más megközelítések, mivel nem elég robusztusak. Egy kis változás az adatokban nagy változást okozhat a végső becsült fában.

A sok döntési fa aggregálásával, olyan módszerek alkalmazásával, mint a bagging, a véletlen erdők és a boosting, a döntési fák előrejelző teljesítménye jelentősen javítható.

Fa alapú módszerek

Bagging

A fent tárgyalt döntési fák nagy szórástól szenvednek, ami azt jelenti, hogy ha a képzési adatokat véletlenszerűen két részre osztjuk, és mindkét felére illesztünk egy döntési fát, a kapott eredmények meglehetősen eltérőek lehetnek. Ezzel szemben egy alacsony varianciájú eljárás hasonló eredményeket fog adni, ha többször alkalmazzuk különböző adathalmazokra.

A zsákolás vagy bootstrap-összevonás egy olyan technika, amelyet a jóslatok varianciájának csökkentésére használunk azáltal, hogy több, ugyanazon adathalmaz különböző almintáin modellezett osztályozó eredményét kombináljuk. Íme a bagging egyenlete:

melyben $B$ különböző bootstrapelt képzési adathalmazokat hoz létre. Ezután a $bth$ bootstrapped gyakorlóhalmazon betanítod a módszeredet, hogy megkapd $\hat{f}_{b}(x)$, és végül átlagolod a jóslatokat.

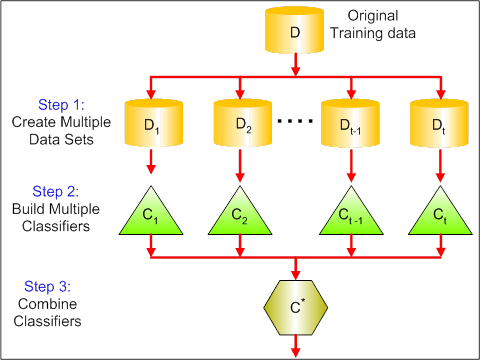
Az alábbi ábrán látható a bagging 3 különböző lépése:

• 1. lépés: Itt az eredeti adatokat új adatokkal helyettesíted. Az új adatok általában az eredeti adatok oszlopainak és sorainak egy töredékével rendelkeznek, amelyek aztán hiperparaméterként használhatók a bagging modellben.

• 2. lépés: Az egyes adathalmazokon osztályozókat építünk. Általában ugyanazt az osztályozót használhatja a modellek és a jóslatok készítéséhez.

• 3. lépés: Végül a problémától függően egy átlagértéket használ az összes osztályozó jóslatának kombinálásához. Általában ezek a kombinált értékek robusztusabbak, mint egyetlen modell.

Míg a zsákolás számos regressziós és osztályozási módszer esetében javíthatja az előrejelzéseket, különösen hasznos a döntési fák esetében. A zsákolás regressziós/osztályozási fákra történő alkalmazásához egyszerűen $B$ regressziós/osztályozási fákat állítunk össze $B$ bootstrapped gyakorlóhalmazok felhasználásával, és az így kapott előrejelzéseket átlagoljuk. Ezeket a fákat mélyre növesztjük, és nem metszünk. Ezért minden egyes fa nagy szórással, de alacsony torzítással rendelkezik. Ezeknek a $B$ fáknak az átlagolása csökkenti a szórást.

Tágabb értelemben a zsákolás bizonyítottan lenyűgöző pontosságjavulást eredményez azáltal, hogy több száz vagy akár több ezer fát egyesít egyetlen eljárásba.

Random Forests

A Random Forests egy sokoldalú gépi tanulási módszer, amely regressziós és osztályozási feladatok elvégzésére egyaránt alkalmas. Dimenziócsökkentő módszereket is vállal, kezeli a hiányzó értékeket, a kiugró értékeket és az adatfeltárás egyéb lényeges lépéseit, és meglehetősen jó munkát végez.

A Random Forests a zsákfákhoz képest javulást nyújt egy kis finomítással, amely dekorrelálja a fákat. A zsákoláshoz hasonlóan a bootstrapped gyakorló mintákon több döntési fát építünk. De amikor ezeket a döntési fákat építjük, minden egyes alkalommal, amikor egy fa felosztását vizsgáljuk, a $p$ prediktorok teljes halmazából egy m prediktorból álló véletlenszerű mintát választunk ki felosztásjelöltként. Az osztás csak egyet használhat ezek közül az $m$ prediktorok közül. Ez a fő különbség a véletlen erdők és a zsákolás között; mivel a zsákoláshoz hasonlóan a prediktor kiválasztása $m = p$.

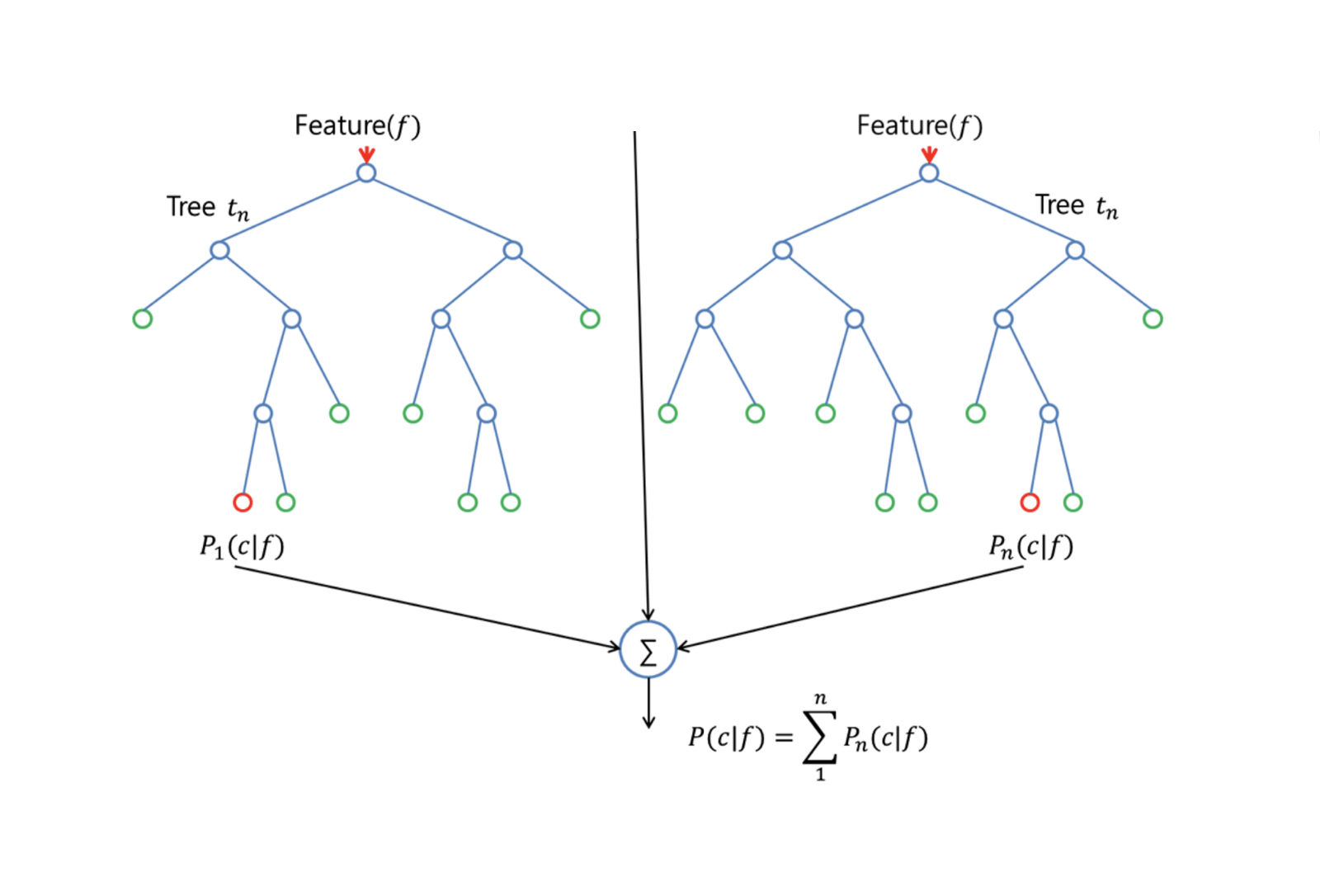
A véletlen erdő növesztéséhez a következőket kell tennünk:

• Először is feltételezzük, hogy a gyakorlóhalmazban az esetek száma K. Ezután vegyünk véletlen mintát ezekből a K esetből, majd ezt a mintát használjuk a fa növesztéséhez a gyakorlóhalmazként.

• Ha $p$ bemeneti változók vannak, adjunk meg egy olyan számot $m < p$, hogy minden csomópontban $m$ véletlen változót választhassunk ki a $p$-ból. Ezeken a $m$-eken a legjobb felosztást használjuk a csomópont felosztására.

• Minden fa ezt követően a lehető legnagyobb mértékben növekszik, és nincs szükség metszésre.

• Végül aggregáljuk a célfák előrejelzéseit az új adatok előrejelzéséhez.

A Random Forests nagyon hatékony a hiányzó adatok becslésében és a pontosság fenntartásában, ha az adatok nagy hányada hiányzik. Olyan adatkészletekben is képes kiegyenlíteni a hibákat, ahol az osztályok kiegyensúlyozatlanok. A legfontosabb, hogy képes kezelni a nagy dimenziójú, masszív adathalmazokat. A Random Forest használatának egyik hátránya azonban, hogy könnyen túlillesztheti a zajos adathalmazokat, különösen abban az esetben, ha regressziót végez.

Boosting

A Boosting egy másik megközelítés a döntési fából származó előrejelzések javítására. A zsákoláshoz és a véletlen erdőkhöz hasonlóan ez is egy általános megközelítés, amely számos statisztikai tanulási módszerre alkalmazható regresszió vagy osztályozás esetén. Emlékezzünk vissza, hogy a zsákolás során az eredeti képzési adathalmaz több példányát hozzuk létre bootstrap segítségével, minden egyes példányhoz külön döntési fát illesztünk, majd az összes fát kombináljuk, hogy egyetlen előrejelző modellt hozzunk létre. Figyelemre méltó, hogy minden egyes fa egy bootstrappelt adathalmazon épül fel, függetlenül a többi fától.

A boosting hasonló módon működik, azzal a különbséggel, hogy a fák növesztése szekvenciálisan történik: minden egyes fa a korábban növesztett fák információinak felhasználásával nő. A Boosting nem tartalmaz bootstrap mintavételt; ehelyett minden egyes fát az eredeti adathalmaz egy módosított változatára illesztünk.

A boosting mind a regressziós, mind az osztályozási fák esetében a következőképpen működik:

• Az egyetlen nagy döntési fa adatokhoz való illesztésével ellentétben, ami az adatok kemény illesztésével és potenciális túlillesztésével egyenlő, a boosting megközelítés ehelyett lassan tanul.

• A jelenlegi modell ismeretében a modell maradékaihoz illeszt egy döntési fát. Ez azt jelenti, hogy egy fát illesztünk, amely a jelenlegi reziduumokat használja válaszként, nem pedig a $Y$ kimenetet.

• Ezt az új döntési fát adjuk hozzá az illesztett függvényhez a reziduumok frissítése érdekében. Mindegyik ilyen fa meglehetősen kicsi lehet, mindössze néhány végcsomóponttal, amelyet az algoritmus $d$ paramétere határoz meg. Azzal, hogy kis fákat illesztünk a reziduumokhoz, lassan javítjuk a $\hat{f}$-t azokon a területeken, ahol az nem teljesít jól.

• A $\nu$ zsugorodási paraméter még tovább lassítja a folyamatot, lehetővé téve, hogy több és különböző alakú fa támadja a reziduumokat.

A döntési fák erősítése nagyon hasznos, ha sok adatunk van, és a döntési fák várhatóan nagyon összetettek lesznek. A Boostingot számos kihívást jelentő osztályozási és regressziós probléma megoldására használták már, többek között kockázatelemzésre, hangulatelemzésre, prediktív reklámra, ármodellezésre, értékesítésbecslésre és betegdiagnózisra.

Döntésfák R-ben

osztályozási fák

Ezért a részért a Carseats adatkészlettel dolgozol az R-ben a tree csomag segítségével. Ne feledd, hogy először telepítened kell a ISLR és tree csomagokat az R Studio környezetedbe. Először töltsük be a Carseats adatkeretet a ISLR csomagból.

library(ISLR)data(package="ISLR")carseats<-Carseats

Töltsük be a tree csomagot is.

require(tree)

A Carseats adatkészlet egy adatkeret 400 megfigyeléssel a következő 11 változóra vonatkozóan:

• Eladás: darabonkénti értékesítés ezerben

• CompPrice: A versenytárs által az egyes helyszíneken felszámított ár

• Jövedelem: a közösség jövedelmi szintje 1000 dollárban

• Hirdetés:

• Népesség: a régió lakossága ezer főben

• Ár: az autóülések ára az egyes helyszíneken

• ShelveLoc: Bad, Good vagy Medium jelzi a polcok helyének minőségét

• Age: a lakosság életkori szintje

• Education: ed szint a helyszínen

• Urban: Igen/Nem

• USA: Igen/Nem

names(carseats)

Nézzük meg az autóeladások hisztogramját:

hist(carseats$Sales)

Nézzük meg, hogy a Sales egy mennyiségi változó. Ezt bináris válasszal rendelkező fák segítségével szeretnénk bemutatni. Ehhez a Sales-t egy bináris változóvá alakítjuk, amelynek a neve High lesz. Ha az értékesítés kevesebb, mint 8, akkor nem lesz magas. Ellenkező esetben magas lesz. Ezután ezt az új High változót visszahelyezhetjük az adatkeretbe.

High = ifelse(carseats$Sales<=8, "No", "Yes")carseats = data.frame(carseats, High)

Most töltsünk ki egy modellt döntési fák segítségével. Természetesen nem lehet itt a Sales változó, mert a High válaszváltozónkat Sales-ból hoztuk létre. Így zárjuk ki, és illesszük be a fát.

tree.carseats = tree(High~.-Sales, data=carseats)

Lássuk az osztályozási fánk összegzését:

summary(tree.carseats)

Láthatjuk az érintett változókat, a végpontok számát, a maradék átlagos eltérést, valamint a téves osztályozási hibaarányt. Hogy szemléletesebbé tegyük, ábrázoljuk a fát is, majd a praktikus text függvény segítségével jegyzeteljük meg:

plot(tree.carseats)text(tree.carseats, pretty = 0)

Ez a sok változó nagyon bonyolulttá teszi a fa megtekintését. Legalább azt láthatjuk, hogy az egyes terminális csomópontoknál Yes vagy No feliratúak. Minden felosztó csomópontnál a változók és a felosztási választás értéke látható (például Price < 92.5 vagy Advertising < 13.5).

A fa részletes összefoglalóját egyszerűen kinyomtathatja. Ez akkor lesz hasznos, ha más célokra részleteket akarunk kinyerni a fából:

tree.carseats

Eljött az ideje a fa lemetszésének. Hozzunk létre egy gyakorló és egy tesztkészletet úgy, hogy a carseats adatkeretet 250 gyakorló és 150 tesztmintára osztjuk. Először is állítsunk be egy magot, hogy az eredmények reprodukálhatók legyenek. Ezután véletlenszerű mintát veszünk a minták azonosító (index) számaiból. Konkrétan itt az 1-től n sorszámú autóülések soraiig terjedő halmazból veszünk mintát, ami 400. 250-es méretű mintát akarsz (alapértelmezés szerint a mintát csere nélkül használja).

set.seed(101)train=sample(1:nrow(carseats), 250)

Így most megkapod ezt a train indexet, amely a 400 megfigyelésből 250-et indexel. A modellt tree-tal újratölthetjük, ugyanezt a képletet használva, kivéve, hogy azt mondjuk a fának, hogy egy részhalmazt használjon, ami egyenlő train-gyel. Ezután készítsünk egy ábrát:

tree.carseats = tree(High~.-Sales, carseats, subset=train)plot(tree.carseats)text(tree.carseats, pretty=0)

A grafikon egy kicsit másképp néz ki a kissé eltérő adathalmaz miatt. Ennek ellenére a fa bonyolultsága nagyjából ugyanúgy néz ki.

Most fogjuk ezt a fát, és a predict fákra vonatkozó módszerrel megjósoljuk a teszthalmazon. Itt valóban a class címkéket akarod majd megjósolni.

tree.pred = predict(tree.carseats, carseats, type="class")

Ezután kiértékelheted a hibát egy téves osztályozási táblázat segítségével.

with(carseats, table(tree.pred, High))

Az átlósokon a helyes osztályozások, míg az átlósokon kívül a helytelen osztályozások vannak. Csak a helyeseket akarja újraértékelni. Ehhez veheted a 2 diagonális összegét osztva az összponttal (150 tesztmegfigyelés).

(72 + 43) / 150

Oké, ezzel a fával 0,76-os hibát kapsz.

Ha nagy bokros fát növesztesz, akkor túl nagy lehet a szórás. Így használjunk keresztvalidálást a fa optimális metszéséhez. A cv.tree segítségével a hibás osztályozási hibát használjuk a metszés elvégzésének alapjául.

cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)cv.carseats

Az eredmények kinyomtatása megmutatja a kereszt-validálás útjának részleteit. Láthatjuk a fák méretét a visszavágás során, az eltéréseket a metszés előrehaladtával, valamint a folyamat során használt költségbonyolultsági paramétert.

Ezt ábrázoljuk ki:

plot(cv.carseats)

A grafikonra pillantva egy lefelé tartó spirális részt látunk a 250 keresztvalidált ponton a téves osztályozási hiba miatt. Válasszunk tehát egy értéket a lefelé irányuló lépcsőfokokon belül (12). Ezután vágjuk le a fát 12-es méretre, hogy azonosítsuk ezt a fát. Végül ábrázoljuk és jegyzeteljük ezt a fát, hogy lássuk az eredményt.

prune.carseats = prune.misclass(tree.carseats, best = 12)plot(prune.carseats)text(prune.carseats, pretty=0)

Ez egy kicsit sekélyebb, mint a korábbi fák, és valóban olvashatók a címkék. Értékeljük ki újra a tesztadatkészleten.

tree.pred = predict(prune.carseats, carseats, type="class")with(carseats, table(tree.pred, High))

(74 + 39) / 150

Úgy tűnik, hogy a helyes osztályozások egy kicsit csökkentek. Körülbelül ugyanúgy teljesített, mint az eredeti fád, tehát a metszés nem sokat ártott a téves osztályozási hibák tekintetében, és egyszerűbb fát adott.

Gyakran előfordul, hogy a fák nem adnak túl jó előrejelzési hibákat, ezért nézzük meg a random erdőket és a boostingot, amelyek általában felülmúlják a fákat, ami az előrejelzést és a téves osztályozást illeti.

Véletlen erdők

Ez a rész a Boston housing data segítségével a random erdőket és a boostingot fogja megvizsgálni. Az adatkészlet a MASS csomagban található. Boston mind az 506 külvárosának lakásértékeit és egyéb statisztikáit adja meg az 1970-es népszámlálás alapján.

library(MASS)data(package="MASS")boston<-Bostondim(boston)names(boston)

Töltsük be a randomForest csomagot is.

require(randomForest)

A véletlen erdőhöz szükséges adatok előkészítéséhez állítsuk be a magot, és hozzunk létre egy 300 megfigyelésből álló minta gyakorlóhalmazt.

set.seed(101)train = sample(1:nrow(boston), 300)

Ez az adathalmaz Boston 506 külvárosát tartalmazza. Minden egyes külvárosra vonatkozóan olyan változók vannak, mint az egy főre jutó bűnözés, az ipar típusai, az egy lakásra jutó szobák átlagos száma, a házak átlagos életkorának aránya stb. Válaszváltozóként használjuk a medv – a saját tulajdonú lakások mediánértékét minden egyes ilyen surburbra vonatkozóan.

Foglaljunk össze egy random forestet, és nézzük meg, milyen jól teljesít. Mint mondottuk, használjuk a medv válaszváltozót, a lakások medián értékét ($1K dollárban) és a képzési mintakészletet.

rf.boston = randomForest(medv~., data = boston, subset = train)rf.boston

A véletlen erdő kinyomtatása megadja annak összegzését: a fák számát (500 fát növesztettek), a reziduumok átlagos négyzetét (MSR) és a megmagyarázott variancia százalékos arányát. Az MSR és a % megmagyarázott variancia a zsákon kívüli becsléseken alapul, ami egy nagyon okos eszköz a random erdőkben, hogy őszinte hiba becsléseket kapjunk.

A random erdők egyetlen hangolási paramétere a mtry nevű argumentum, ami az egyes fák minden osztásánál kiválasztott változók száma, amikor osztást készítünk. Amint itt látható, az mtry 4 a 13 feltáró változóból (a medv kivételével) a bostoni lakásadatokban – ami azt jelenti, hogy minden alkalommal, amikor a fa egy csomópont felosztásához érkezik, 4 változót választ ki véletlenszerűen, majd a felosztás e 4 változó közül 1-re korlátozódik. Így a randomForests korrelációmentesíti a fákat.

Egy sor véletlen erdő illesztését fogja elvégezni. 13 változó van, tehát legyen mtry 1 és 13 között:

• A hibák rögzítésére 2 változót állítasz be oob.err és test.err.

• Az mtry 1 és 13 közötti ciklusban először a randomForest-et illeszted a train adathalmazon ezzel az mtry értékkel, a fák számát 350-re korlátozva.

• Ezután kivonod az objektumra vonatkozó átlagos négyzetes hibát (a zsákon kívüli hibát).

• Ezután a tesztadathalmazon (boston) a fit (a randomForest illesztése) segítségével jósolsz.

• Végül kiszámítod a teszthibát: átlagos négyzetes hiba, ami egyenlő mean( (medv - pred) ^ 2 ).

oob.err = double(13)test.err = double(13)for(mtry in 1:13){ fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350) oob.err = fit$mse pred = predict(fit, boston) test.err = with(boston, mean( (medv-pred)^2 ))}

Gyakorlatilag most növesztettél 4550 fát (13-szor 350). Most készítsünk egy ábrát a matplot parancs segítségével. A teszthibát és a zsákon kívüli hibát kössük össze egy 2 oszlopos mátrixba. A mátrixban van még néhány argumentum, többek között a plotting karakter értékei (pch = 23 azt jelenti, hogy kitöltött rombusz), a színek (piros és kék), a type equals both (mindkét pontot kirajzolja és összeköti a vonalakkal), és az y-tengely neve (Mean Squared Error). A grafikon jobb felső sarkában egy legendát is elhelyezhet.

matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))

Ezeknek a 2 görbének igazából egy vonalba kellene kerülniük, de úgy tűnik, hogy a teszt hibája egy kicsit alacsonyabb. Azonban ezekben a teszthiba becslésekben nagy a szórás. Mivel a zsákon kívüli hiba becslését egy adathalmazon, a teszthiba becslését pedig egy másik adathalmazon számították ki, ezek a különbségek nagyjából a standard hibákon belül vannak.

Észrevetted, hogy a piros görbe simán a kék görbe fölött van? Ezek a hiba becslések nagyon korrelálnak, mert a randomForest a mtry = 4-vel nagyon hasonló a mtry = 5-vel. Ezért van az, hogy mindegyik görbe meglehetősen sima. Azt látod, hogy a 4 körüli mtry tűnik a legoptimálisabb választásnak, legalábbis a teszthiba szempontjából. Ez az mtry érték a zsákon kívüli hiba esetében 9,

Szóval nagyon kevés réteggel egy nagyon erős előrejelzési modellt illesztettünk be a véletlen erdők segítségével. Hogyan? A baloldalon egyetlen fa teljesítménye látható. Az out-of-bag átlagos négyzetes hibája 26, és körülbelül 15-re csökkentetted (valamivel a fele fölé). Ez azt jelenti, hogy felére csökkentette a hibát. Hasonlóképpen a teszthiba esetében is csökkentetted a hibát 20-ról 12-re.

Boosting

A véletlen erdőkhöz képest a boosting kisebb és csonka fákat növeszt, és az előfeszítésre megy rá. A GBM (Gradient Boosted Modeling) csomagot fogod használni, az R-ben.

require(gbm)

GBM kéri az eloszlást, ami Gauss, mert négyzetes hibaveszteséget fogsz csinálni. A GBM-től 10 000 fát fogsz kérni, ami soknak hangzik, de ezek sekély fák lesznek. Az interakciós mélység a hasítások száma, tehát minden fában 4 hasítást akarsz. A zsugorítás 0,01, ami azt jelenti, hogy mennyivel fogod visszaszorítani a fa lépését.

boost.boston = gbm(medv~., data = boston, distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)summary(boost.boston)

A summary függvény egy változó fontossági ábrát ad. Úgy tűnik, hogy van 2 olyan változó, amelynek nagy a relatív fontossága: rm (a szobák száma) és lstat (az alacsonyabb gazdasági státuszú emberek aránya a közösségben). Ábrázoljuk ezt a 2 változót:

plot(boost.boston,i="lstat")plot(boost.boston,i="rm")

Az 1. ábrán látható, hogy minél magasabb az alacsonyabb státuszú emberek aránya a külvárosban, annál alacsonyabb a lakásárak értéke. A 2. grafikon a szobák számával való fordított összefüggést mutatja: a házban lévő szobák átlagos száma nő az ár növekedésével.

Eljött az ideje, hogy a tesztadathalmazon megjósoljuk a boostolt modellt. Nézzük meg a tesztteljesítményt a fák számának függvényében:

• Először is készítsünk egy rácsot a fák számából 100-as lépésekben 100-tól 10 000-ig.

• Ezután futtassuk a predict függvényt a boostolt modellen. A n.trees argumentumot veszi fel, és a tesztadatokra vonatkozó előrejelzések mátrixát állítja elő.

• A mátrix dimenziói 206 tesztmegfigyelés és 100 különböző előrejelzési vektor a fa 100 különböző értékénél.

  n.trees = seq(from = 100, to = 10000, by = 100)predmat = predict(boost.boston, newdata = boston, n.trees = n.trees)dim(predmat)

Az egyes prediktív vektorok teszthibájának kiszámítása következik:

• predmat egy mátrix, medv egy vektor, tehát (predmat – medv) egy különbségmátrix. A apply függvényt használhatjuk ezeknek a négyzetes különbségeknek az oszlopaira (az átlagra). Ez kiszámítja a prediktív vektorok oszloponkénti átlagos négyzetes hibáját.

• Ezután a Random Forest esetében használthoz hasonló paraméterekkel készíthet egy ábrát. Ez egy boosting error plotot mutatna.

  boost.err = with(boston, apply( (predmat - medv)^2, 2, mean) )plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")abline(h = min(test.err), col = "red")

A boosting error nagyjából lecsökken a fák számának növekedésével. Ez azt bizonyítja, hogy a boosting vonakodik a túlillesztéstől. Vegyük be az ábrába a randomForest legjobb teszthibáját is. A boosting valóban ésszerű mértékben kerül a randomForest teszthibája alá.

Következtetés

Ezzel véget ért ez az R bemutató a döntési fák modelljeinek építéséről: osztályozófák, véletlen erdők és boostolt fák. Az utóbbi 2 nagy teljesítményű módszer, amelyeket szükség szerint bármikor használhatsz. Tapasztalataim szerint a boosting általában felülmúlja a RandomForestet, de a RandomForestet könnyebb implementálni. A RandomForestben az egyetlen hangolási paraméter a fák száma; míg a boostingban a fák számán kívül több hangolási paraméterre van szükség, beleértve a zsugorítást és a kölcsönhatás mélységét.

Ha többet szeretne megtudni, mindenképpen nézze meg a Machine Learning Toolbox for R kurzusunkat.