• Logisztikus regressziós egyenlet
• Logisztikus regresszió. B-koefficiensek
• Logisztikus regresszió – hatásméret
• Logisztikus regresszió feltételezések

A logisztikus regresszió egy olyan technika, amellyel egy
dichotóm kimeneti változót 1+ prediktorokból lehet megjósolni.Példa: Milyen valószínűséggel halnak meg emberek 2020 előtt, ha a 2015-ös életkorukat vesszük alapul? Vegyük észre, hogy a “meghalni” dichotóm változó, mivel csak 2 lehetséges kimenete van (igen vagy nem).
Ezt az elemzést bináris logisztikus regressziónak vagy egyszerűen “logisztikus regressziónak” is nevezik. Egy kapcsolódó technika a multinomiális logisztikus regresszió, amely 3+ kategóriával rendelkező kimeneti változókat jósol.

Logisztikus regresszió – egyszerű példa

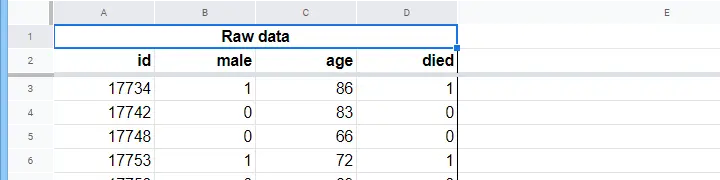
Egy idősek otthona rendelkezik adatokkal N = 284 ügyfél neméről, 2015. január 1-jei életkoráról és arról, hogy az ügyfél 2020. január 1-je előtt elhunyt-e. A logisztikus regresszió a következő adatokkal rendelkezik. A nyers adatok ebben a Googlesheetben vannak, részben az alábbiakban láthatóak.

Fókuszáljunk először csak az életkorra:a 2015-ös életkorból megjósolható a 2020 előtti halálozás?És -ha igen- pontosan hogyan? És milyen mértékben? Egy jó első lépés egy olyan szórásdiagram vizsgálata, mint az alábbiakban látható.

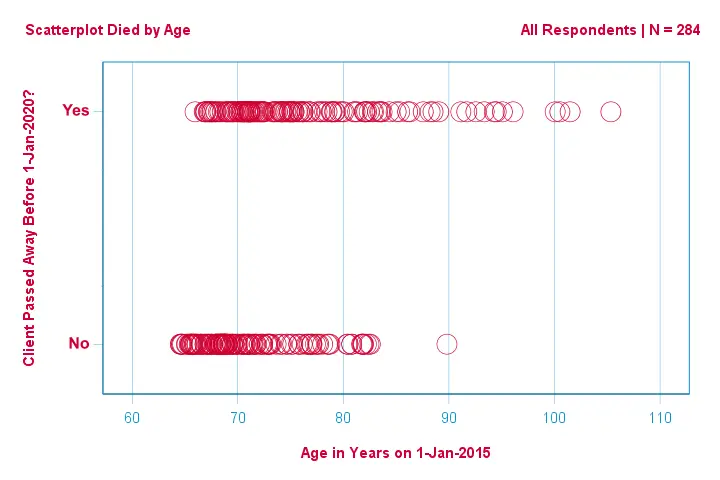
Ebben a szórásdiagramban néhány dolgot látunk:

• egy kivételével minden 83 évnél idősebb ügyfél meghalt a következő 5 évben;
• az életkor szórása sokkal nagyobb a meghalt ügyfeleknél, mint a túlélőknél;
• az életkor jelentős pozitív ferdeséggel rendelkezik, különösen a meghalt ügyfeleknél.

De hogyan tudjuk megjósolni, hogy egy ügyfél meghalt-e, ha ismerjük az életkorát? Éppen ezt fogjuk megtenni egy logisztikus görbe illesztésével.

Egyszerű logisztikus regressziós egyenlet

Az egyszerű logisztikus regresszió kiszámítja valamilyen kimenetel valószínűségét egyetlen prediktor változó mellett a következőképpen

$$P(Y_i) = \frac{1}{1 + e^{\\,-\\,(b_0\,+\,b_1X_{1i})}}}$$

ahol

• \(P(Y_i)\) az a megjósolt valószínűség, hogy \(Y\) igaz \(i\) esetben;
• \(e\) egy matematikai konstans, amely nagyjából 2.72;
• \(b_0\) az adatokból becsült konstans;
• \(b_1\) az adatokból becsült b együttható;
• \(X_i\) az \(X\) változó megfigyelt eredménye az \(i\) esetben.

A logisztikus regresszió lényege az \(b_0\) és \(b_1\) becslése. Ez a 2 szám lehetővé teszi számunkra, hogy kiszámítsuk egy ügyfél halálának valószínűségét bármely megfigyelt életkor mellett. Ezt néhány példagörbével illusztráljuk, amelyeket az előző szórásdiagramhoz adtunk hozzá.

Logisztikus regresszió példagörbéi

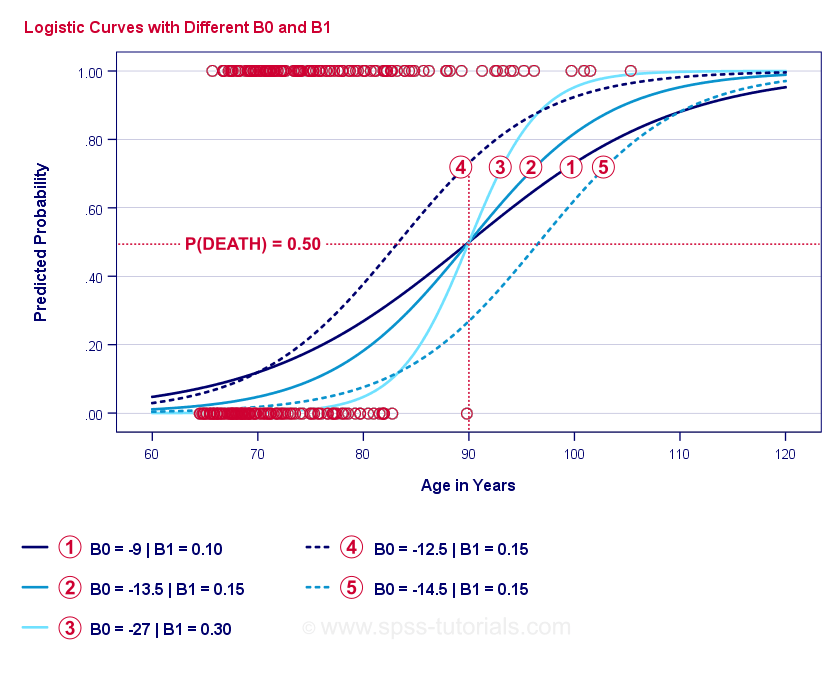
Ha szán egy percet e görbék összehasonlítására, a következőket láthatja:

• \(b_0\) határozza meg a görbék vízszintes helyzetét: ahogy \(b_0\) nő, a görbék balra tolódnak, de a meredekségük nem változik. Ez a , és görbék esetében látható. Vegyük észre, hogy \(b_0\) különböző, de \(b_1\) egyenlő ezeknél a görbéknél.
• Amint nő az \(b_0\), úgy nő a megjósolt valószínűség is: 90 éves kor esetén a görbe nagyjából 0,75 valószínűséget jósol a halálozásra. A és görbék nagyjából 0,50 és 0,25 valószínűséget jósolnak a halálozásra egy 90 éves ügyfél esetében.
• \(b_1\) határozza meg a görbék meredekségét: ha \(b_1\) > 0, a halálozás valószínűsége az életkor növekedésével nő. Ez az összefüggés annál erősebb lesz, minél nagyobb \(b_1\). A , és görbék szemléltetik ezt a pontot: ahogy \(b_1\) nagyobb lesz, a görbék meredekebbek lesznek, így a halálozás valószínűsége gyorsabban nő az életkor növekedésével.

Egy kérdés maradt hátra: hogyan találjuk meg a “legjobb” \(b_0\) és \(b_1\) értékeket?

Logisztikus regresszió – Log Likelihood

A logisztikus regressziós modell minden egyes válaszadó esetében megbecsüli annak valószínűségét, hogy valamilyen \(Y_i\) esemény bekövetkezett. Nyilvánvaló, hogy ezeknek a valószínűségeknek magasnak kell lenniük, ha az esemény valóban bekövetkezett, és fordítva. Az egyik módja annak, hogy összefoglaljuk, mennyire jól teljesít valamilyen modell az összes válaszadó esetében, a log-likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$$

hol

• \(Y_i\) 1, ha az esemény bekövetkezett, és 0, ha nem;
• \(ln\) a természetes logaritmust jelöli: milyen hatványra kell emelni \(e\), hogy egy adott számot kapjunk?

\(LL\) az illeszkedés jóságának mérőszáma: ha minden más nem változik, a logisztikus regressziós modell jobban illeszkedik az adatokhoz, amennyiben \(LL\) nagyobb. Kissé zavaró módon az \(LL\) mindig negatív. Tehát azt az \(b_0\) és \(b_1\) értéket akarjuk megtalálni, amelyhez
\(LL\) a lehető legközelebb van a nullához.

Maximum Likelihood Estimation

A lineáris regresszióval ellentétben a logisztikus regresszió nem tudja könnyen kiszámítani az \(b_0\) és \(b_1\) optimális értékeit. Ehelyett különböző számokat kell kipróbálnunk, amíg az \(LL\) nem növekszik tovább. Minden ilyen kísérletet iterációnak nevezünk. Az ilyen iterációkon keresztül történő optimális értékek megtalálásának folyamatát maximum likelihood becslésnek nevezzük.

Az alapvetően így kapják meg a statisztikai szoftverek – mint például az SPSS, a Stata vagy a SAS – a logisztikus regresszió eredményeit. Szerencsére elképesztően jók ebben. De ahelyett, hogy \(LL\) értéket adnának meg, ezek a csomagok \(-2LL\) értéket adnak meg.Az \(-2LL\) egy “badness-of-fit” mérték, amely egy
chi-négyzet-eloszlást követ.Ez teszi az \(-2LL\) értéket hasznosnak a különböző modellek összehasonlítására, amint azt rövidesen látni fogjuk. Az \(-2LL\) az alább látható kimeneten -2 Log likelihoodként van jelölve.

A lábjegyzetből megtudhatjuk, hogy a maximális valószínűségű becslésnek mindössze 5 iterációra volt szüksége az optimális b-koefficiensek \(b_0\) és \(b_1\) megtalálásához. Nézzük meg tehát most ezeket.

Logisztikus regresszió – B-koefficiensek

Minden logisztikus regressziós elemzés legfontosabb kimenete a b-koefficiensek. Az alábbi ábra mutatja őket a példánk adataira.

Mielőtt belemennénk a részletekbe, ez a kimenet röviden megmutatja

a modellünket alkotó b-koefficienseket;
e b-koefficiensek standard hibáit;
a Wald-statisztikát – amelyet \((\frac{B}{SE})^2\)-ként számítunk ki-négyzet eloszlást követ;
a Wald-statisztika szabadságfokai;
a b-koefficiensek szignifikancia-szintjei;
az exponenciált b-koefficiensek vagy \(e^B\) a prediktor-értékek változásához kapcsolódó esélyhányadosok;
az exponenciált b-koefficiensek 95%-os konfidenciaintervalluma.

A b-koefficiensek kiegészítik logisztikus regressziós modellünket, amely most

$$$P(halál_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, age_i)}}}$$

Egy 75 éves ügyfél esetében annak valószínűsége, hogy 5 éven belül meghal

$$P(halál_i) = \frac{1}{1 + e^{\\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}}=$$

$$P(halál_i) = \frac{1}{1 + e^{\,-\,0.249}}}=$$

$$$P(halál_i) = \frac{1}{1 + 0.780}=$$

$$$P(halál_i) \approx 0.562$$

Szóval most már tudjuk, hogyan lehet megjósolni a halálozást 5 éven belül valakinek az életkora alapján. De mennyire jó ez a jóslat? Többféle megközelítés létezik. Kezdjük a modell-összehasonlításokkal.

Logisztikus regresszió – alapmodell

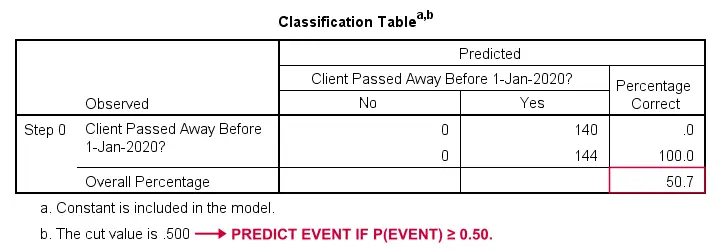
Hogyan tudnánk megjósolni, hogy ki hunyt el, ha semmilyen más információnk nincs? Nos, a mintánk 50,7%-a hunyt el. Tehát a megjósolt valószínűség egyszerűen 0,507 lenne mindenki esetében.

Az osztályozáshoz általában akkor jósoljuk meg, hogy egy esemény bekövetkezik, ha p(esemény) ≥ 0,50. Mivel p(meghalt) = 0,507 mindenki esetében, egyszerűen azt jósoljuk, hogy mindenki meghalt. Ez az előrejelzés helyes a mintánk 50,7%-ára, akik meghaltak.

Logisztikus regresszió – valószínűségi hányados

Most, ezekből az előrejelzett valószínűségekből és a megfigyelt eredményekből kiszámíthatjuk a rossz illeszkedés mértékét: -2LL = 393,65. A tényleges modellünk – amely az életkorból eredő halálozást jósolja – -2LL = 354,20 értéket kap. A két szám közötti különbséget nevezzük valószínűségi aránynak \(LR\):

$$LR = (-2LL_{alapeset}) – (-2LL_{modell})$$

Fontos, hogy \(LR\) egy chi-négyzet eloszlást követ \(df\) szabadsági fokokkal, a következőképpen számítjuk ki:

$$df = k_{modell} – k_{alapeset}$$

ahol \(k\) a modellek által becsült paraméterek számát jelöli. Ahogy ebben a Googlesheetben látható, \(LR\) és \(df\) a teljes modell szignifikancia szintjét eredményezi.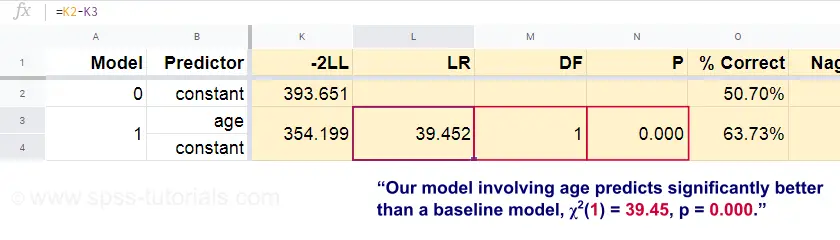

A nullhipotézis itt az, hogy valamely modell ugyanolyan rosszul jósol, mint az alapmodell valamely populációban. Mivel p = 0,000, ezt elutasítjuk: a mi modellünk (a halálozást az életkor alapján előrejelző) szignifikánsan jobban teljesít, mint a prediktorok nélküli alapmodell.
De pontosan mennyivel jobban? Erre a választ a hatásmérete adja meg.

Logisztikus regresszió – Modell hatásmérete

A hatásméret alapján jól értékelhető, hogy modellünk mennyire jól teljesít. Az egyik lehetőség a Cox & Snell R2 vagy \(R^2_{CS}\), amelyet a következőképpen számítunk ki:

$$$R^2_{CS} = 1 – e^{\frac{(-2LL_{modell})\,-\,(-2LL_{alap})}{n}}$$

Sajnos az \(R^2_{CS}\) soha nem éri el az 1 elméleti maximumot. Ezért gyakran előnyben részesítik a Nagelkerke R2 vagy \(R^2_{N}\) néven ismert korrigált változatot:

$$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{alapvonal}}}{n}}}$$

Példánk adataira \(R^2_{CS}\) = 0,130, ami közepes hatásméretet jelez. \(R^2_{N}\) = 0,173, ami valamivel nagyobb a közepesnél.

Az \(R^2_{CS}\) és az \(R^2_{N}\) technikailag teljesen különbözik a lineáris regresszióban számított r-négyzettől. Azonban ugyanazt a szerepet próbálják betölteni. Ezért mindkét mértéket pszeudo r-négyzet mértéknek nevezzük.

Logisztikus regresszió – prediktor hatásméret

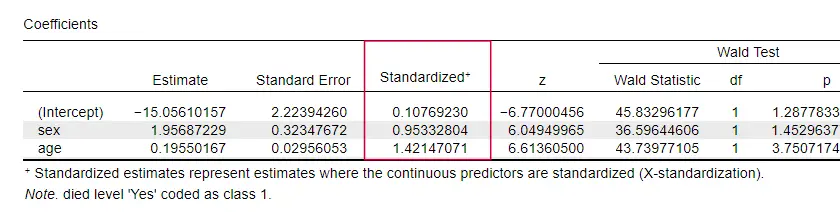
Nagyon kevés tankönyv említi az egyes prediktorokra vonatkozó hatásméretet. Talán azért, mert ezek teljesen hiányoznak az SPSS-ből. Azért van rájuk szükségünk, mert a b-koefficiensek a prediktoraink (tetszőleges) skáláitól függnek: ha az életkort év helyett napokban adnánk meg, a b-koefficiense óriási mértékben zsugorodna. Ez nyilvánvalóan alkalmatlanná teszi a b-koefficienseket a prediktorok összehasonlítására a különböző modelleken belül vagy azok között.
A JASP részben standardizált b-koefficienseket tartalmaz: a kvantitatív prediktorokat – de nem a kimeneti változót – z-értékek formájában adjuk meg, ahogy az alább látható.

Logisztikus regresszió feltételezései

A logisztikus regresszióelemzés a következő feltételezéseket követeli meg:

1. független megfigyelések;
2. korrekt modellspecifikáció;
3. a kimeneti változó és az összes prediktor hibamentes mérése;
4. linearitás: minden prediktor lineárisan kapcsolódik \(e^B\) (az esélyhányadoshoz).

A 4. feltételezés némileg vitatható, és számos tankönyv1,6 kihagyja. A Field4 által tárgyalt Box-Tidwell-teszttel értékelhető. Ez lényegében annak tesztelésére fut ki, hogy van-e kölcsönhatás az egyes prediktorok és azok természetes logaritmusa vagy \(LN\) között.

Multiple Logistic Regression

Ezidáig a tárgyalásunk az egyszerű logisztikus regresszióra korlátozódott, amely csak egy prediktort használ. A modell könnyen kibővíthető további prediktorokkal, ami többszörös logisztikus regressziót eredményez:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,….+\,b_kX_{ki})}}$$

hol

• \(P(Y_i)\) az a megjósolt valószínűség, hogy \(Y\) igaz \(i\) esetben;
• \(e\) egy nagyjából 2-es matematikai állandó.72;
• \(b_0\) az adatokból becsült konstans;
• \(b_1\), \(b_2\), … ,\(b_k\) az 1., 2., … prediktorokra vonatkozó b-koefficiensek. ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) az \(X_1\), \(X_2\), … prediktorokra vonatkozó megfigyelt pontszámok. ,\(X_k\) az \(i\) esetre.

A többszörös logisztikus regresszió gyakran magában foglalja a modell kiválasztását és a multikollinearitás ellenőrzését. Ettől eltekintve ez egy meglehetősen egyszerű kiterjesztése az egyszerű logisztikus regressziónak.

Ez az alapvető bevezetés a logisztikus regresszió lényegére korlátozódott. Ha többet szeretne megtudni, érdemes utánaolvasnia néhány kihagyott témának:

1. a logisztikus regresszióban \(e^B\)-ként kiszámított esélyhányadosok kifejezik, hogyan változnak a valószínűségek a prediktorértékek függvényében;
2. a Box-Tidwell-teszt azt vizsgálja, hogy a fent említett esélyhányadosok és a prediktorértékek közötti kapcsolatok lineárisak-e;
3. a Hosmer és Lemeshow-teszt egy alternatív illeszkedési jósági teszt a teljes logisztikus regressziós modellre.

Köszönjük az olvasást!

1. Warner, R.M. (2013). Alkalmazott statisztika (2. kiadás). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statisztika. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis (Többváltozós adatelemzés). New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statisztikai módszerek a pszichológia számára (5. kiadás). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6. kiadás). New York: Routledge.