Iniziamo lo studio delle equazioni differenziali parziali con il problema del flusso di calore in una barra uniforme di lunghezza \(L\), situata sull’asse \(x\) con un’estremità nell’origine e l’altra in \(x = L\) (figura \(\PageIndex{1}).
Assumiamo che la barra sia perfettamente isolata, tranne eventualmente ai suoi estremi, e che la temperatura sia costante su ogni sezione e quindi dipenda solo da \(x\) e \(t\). Assumiamo anche che le proprietà termiche della barra siano indipendenti da \(x\) e \(t\). In questo caso, si può dimostrare che la temperatura \(u = u(x, t)\) al tempo \(t\) in un punto \(x\) unità dall’origine soddisfa l’equazione differenziale parziale
dove \(a\) è una costante positiva determinata dalle proprietà termiche. Questa è l’equazione del calore.
Per determinare \(u), dobbiamo specificare la temperatura in ogni punto della barra quando \(t=0\), diciamo
\
Chiamiamo questa la condizione iniziale. Dobbiamo anche specificare le condizioni limite che \(u\) deve soddisfare alle estremità della barra per tutti i \(t>0\). Chiameremo questo problema un problema di valore iniziale-limite.
Iniziamo con le condizioni limite \(u(0,t)=u(L,t)=0\), e scriviamo il problema di valore iniziale-limite come
\
Il nostro metodo per risolvere questo problema è chiamato separazione delle variabili (da non confondere con il metodo di separazione delle variabili usato nella Sezione 2.2 per risolvere le equazioni differenziali ordinarie). Cominciamo a cercare funzioni della forma
\
che non siano identicamente zero e che soddisfino
\
per tutti i \((x,t)\). Siccome
\
(v_t=a^2v_{xx}\) se e solo se
\
che riscriviamo come
\
Siccome l’espressione a sinistra è indipendente da \(x\) mentre quella a destra è indipendente da \(t\), questa equazione può valere per tutti i \((x,t)\) solo se i due lati sono uguali alla stessa costante, che chiamiamo costante di separazione, e la scriviamo come \(-lambda\); Quindi,
Questo è equivalente a
e
Siccome \(v(0,t)=X(0)T(t)=0\) e \(v(L,t)=X(L)T(t)=0\) e non vogliamo che \(T\) sia identicamente zero, \(X(0)=0\) e \(X(L)=0\). Quindi \(\lambda\) deve essere un autovalore del problema dei valori limite
e \(X\) deve essere una funzione propria di \(\lambda\). Dal Teorema 11.1.2, gli autovalori dell’equazione \ref{eq:12.1.3} sono \(\lambda_n=n^2\pi^2/L^2\), con associate autofunzioni
\
Sostituendo \(\lambda=n^2\pi^2/L^2\) nell’equazione \ref:12.1.2} si ottiene
che ha la soluzione
Ora sia
Siccome
\(v_n\) soddisfa l’equazione \ref{eq:12.1.1} con \(f(x)=sin n\pi x/L\). Più in generale, se \(\alfa_1,\punti,\alfa_m\) sono costanti e
\
allora \(u_m\) soddisfa l’equazione \ref{eq:12.1.1} con
\
Questo motiva la prossima definizione.
Teorema \(\PageIndex{1})
La soluzione formale del problema dei valori inizialiLa soluzione formale del problema di valore iniziale e limite
è
dove
è la serie sinusoidale di Fourier di \(f\) su \(\); cioè
Usiamo il termine “soluzione formale” in questa definizione perché non è in generale vero che la serie infinita dell’equazione \ref{eq:12.1.5} soddisfi effettivamente tutti i requisiti del problema del valore limite iniziale dell’equazione \ref{eq:12.1.4} quando lo fa, diciamo che è una soluzione effettiva dell’equazione \ref{eq:12.1.4}.
A causa degli esponenziali negativi nell’equazione \ref{eq:12.1.5}, \(u\) converge per tutti \((x,t)\) con \(t>0\) (Esercizio 12.1.54). Poiché ogni termine dell’equazione \ref{eq:12.1.5} soddisfa l’equazione del calore e le condizioni al contorno dell’equazione \ref{eq:12.1.4}, \(u) ha anche queste proprietà se \(u_t\) e \(u_xx}) possono essere ottenuti differenziando la serie dell’equazione \ref{eq:12.1.5} termine per termine una volta rispetto a \(t\) e due volte rispetto a \(x\), per \(t>0\). Tuttavia, non è sempre legittimo differenziare una serie infinita termine per termine. Il prossimo teorema fornisce un’utile condizione sufficiente per la legittimità della differenziazione termine per termine di una serie infinita. Omettiamo la dimostrazione.
Teorema \(\PageIndex{2})
Una serie infinita convergente
può essere differenziata termine per termine su un intervallo chiuso \(\) per ottenere
((\) dove le derivate a \(z=z_1\) e \(z=z_2\) sono una condizione che \(w_n’\) sia continua su \(\) e
dove \(M_1,\) \(M_2,\) …, \(M_n,\) …, sono costanti tali che la serie \(\sum_{n=1}^\infty M_n\) converge.
Il teorema \PageIndex{2}, applicato due volte con \(z=x) e una volta con \(z=t), mostra che \(u_xx}) e \(u_t) possono essere ottenuti differenziando \(u\) termine per termine se \(t>0\) (Esercizio 12.1.54). Quindi \(u\) soddisfa l’equazione del calore e le condizioni al contorno dell’equazione \ref{eq:12.1.4} per \(t>0\). Quindi, poiché \(u(x,0)=S(x)\) per \(0\le x\le L\), \(u\) è una soluzione effettiva dell’equazione \ref{eq:12.1.4} se e solo se \(S(x)=f(x)\) per \(0\le x\le L\). Dal Teorema 11.3.2, questo è vero se \(f\) è continuo e uniforme su \(\), e \(f(0)=f(L)=0\).
In questo capitolo definiremo soluzioni formali di diversi tipi di problemi. Quando vi chiediamo di risolvere tali problemi, intendiamo sempre che dovete trovare una soluzione formale.
Esempio \(\PageIndex{1})
Solvere l’equazione \ref{eq:12.1.4} con \(f(x)=x(x^2-3Lx+2L^2)\).
Soluzione
Dall’esempio \) è
Quindi
Se entrambe le estremità della barra sono isolate in modo che il calore non possa passarvi attraverso, allora le condizioni al contorno sono
Lasciamo a voi (Esercizio 12.1.1) di usare il metodo della separazione delle variabili e il teorema 11.1.3 per motivare la prossima definizione.
Teorema \(\PageIndex{3})
La soluzione formale del problema del valore limite iniziale
è
dove
è la serie coseno di Fourier di \(f\) su \(;\) che è,
Esempio \(\PageIndex{2})
Solve l’equazione \ref{eq:12.1.6} con \(f(x)=x\).
Soluzione
Dall’esempio 11.3.1, la serie coseno di Fourier di \(f\) su \(\) è
Perciò
Lasciamo a voi (Esercizio 12.1.2) di usare il metodo della separazione delle variabili e il teorema 11.1.4 per motivare la prossima definizione.
Teorema \(\PageIndex{4})
La soluzione formale del problema del valore limite iniziale
è
dove
è la serie sinusoidale mista di Fourier di \(f\) su \(;\) che è,
Esempio \(\PageIndex{3})
Solve l’equazione \ref{eq:12.1.7} con \(f(x)=x\).
Soluzione
Dall’esempio 11.3.4, la serie sinusoidale mista di Fourier di \(f) su \(\) è
Pertanto
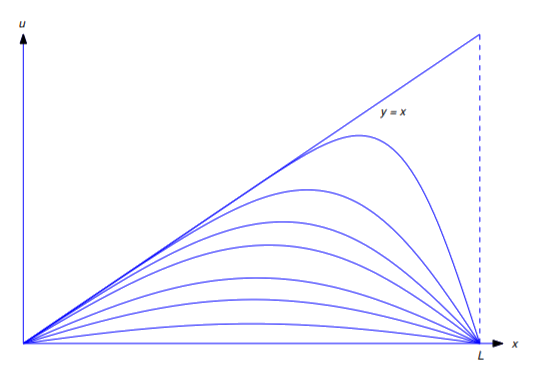
La figura \(\PageIndex{2}\ mostra un grafico di \(u=u(x,t)\ tracciato rispetto a \(x\) per vari valori di \(t\). La linea \(y=x\) corrisponde a \(t=0\). Le altre curve corrispondono a valori positivi di \(t). All’aumentare di \(t), i grafici si avvicinano alla retta \(u=0\).
Lasciamo a voi (Esercizio 12.1.3) di usare il metodo della separazione delle variabili e il Teorema 11.1.5 per motivare la prossima definizione.
Teorema \(\PageIndex{5})
La soluzione formale del problema dei valori inizialiLa soluzione formale del problema di valore iniziale e limite
è
dove
è la serie coseno mista di Fourier di \(f\) su \(\); cioè,
Esempio \(\PageIndex{4})
Solve l’equazione \ref{eq:12.1.8} con \(f(x)=x-L\).
Soluzione
Dall’esempio 11.3.3, la serie coseno mista di Fourier di \(f\) su \(\) è
Quindi
Utilizzare la tecnologia
Gli esperimenti numerici possono migliorare la comprensione delle soluzioni dei problemi di valore limite iniziale. Per essere specifici, considerate la soluzione formale
dell’equazione \ref{eq:12.1.4}, dove
è la serie seno di Fourier di \(f\) su \(\). Si consideri l’ennesima somma parziale
per diversi valori fissi di \(t\) (incluso \(t=0\)), il grafico \(u_m(x,t)\) rispetto a \(t\). In alcuni casi può essere utile tracciare le curve corrispondenti ai vari valori di \t\ sugli stessi assi, in altri casi si può desiderare di tracciare le varie curve successivamente (per valori crescenti di \t\), e creare un’immagine primitiva di movimento sul vostro monitor. Ripeti questo esperimento per diversi valori di \(m), per confrontare come i risultati dipendono da \(m) per valori piccoli e grandi di \(t). Comunque, tieni a mente che il significato di “piccolo” e “grande” in questo caso dipende dalle costanti \(a^2\) e \(L^2\). Un buon modo per gestire questo è quello di riscrivere l’equazione \ref{eq:12.1.12} come
\
dove
\
e graficare \(u_m\) contro \(x\) per valori selezionati di \(\tau\).
Questi commenti si applicano anche alle situazioni considerate nei teoremi \(\PageIndex{3})-(\PageIndex{5}), tranne che l’equazione \ref{eq:12.1.13} dovrebbe essere sostituita da
nei teoremi \(\PageIndex{4}) e \(\PageIndex{5}).