• Equazione della regressione logistica
• Curve di esempio di regressione logistica
• Regressione logistica – Grandezza d’effetto
• Consupposti della regressione logistica

Regressione logistica B-Coefficienti

Regressione logistica – Dimensione dell’effetto

Previsioni della regressione logistica

La regressione logistica è una tecnica per predire una variabile di risultato dicotomica da 1+ predittori.Esempio: quanta probabilità hanno le persone di morire prima del 2020, data la loro età nel 2015? Si noti che “morire” è una variabile dicotomica perché ha solo 2 possibili risultati (sì o no).
Questa analisi è anche conosciuta come regressione logistica binaria o semplicemente “regressione logistica”. Una tecnica correlata è la regressione logistica multinomiale che predice le variabili di risultato con 3+ categorie.

Regressione logistica – Esempio semplice

Una casa di cura ha dati sul sesso di N = 284 clienti, l’età al 1° gennaio 2015 e se il cliente è morto prima del 1° gennaio 2020. I dati grezzi sono in questo Googlesheet, in parte mostrato qui sotto.

Prima concentriamoci solo sull’età: possiamo prevedere la morte prima del 2020 dall’età nel 2015? E – se sì – precisamente come? E in che misura? Un buon primo passo è l’ispezione di un grafico di dispersione come quello mostrato qui sotto.

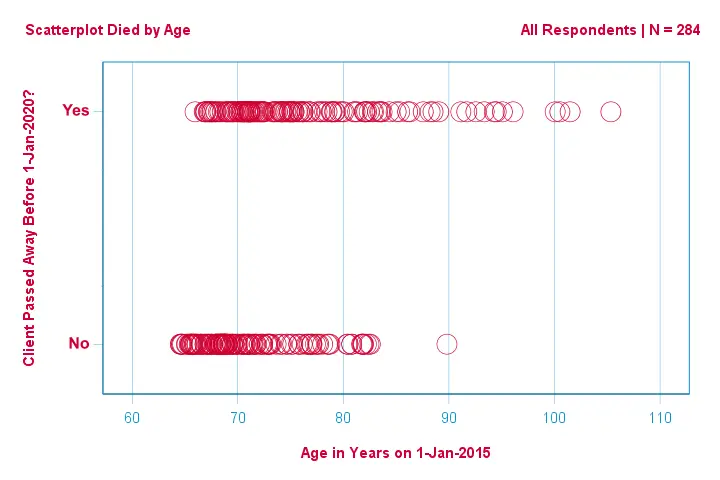
Alcune cose che vediamo in questo grafico di dispersione sono che

• tutti i clienti di età superiore a 83 anni tranne uno sono morti entro i prossimi 5 anni;
• la deviazione standard dell’età è molto più grande per i clienti che sono morti che per i clienti che sono sopravvissuti;
• l’età ha una notevole asimmetria positiva, specialmente per i clienti che sono morti.

Ma come possiamo prevedere se un cliente è morto, data la sua età? Faremo proprio questo adattando una curva logistica.

Equazione di regressione logistica semplice

La regressione logistica semplice calcola la probabilità di qualche risultato data una singola variabile predittiva come

$$P(Y_i) = \frac{1}{1 + e^{\,

$

dove

• \(P(Y_i)\è la probabilità prevista che \(Y_i)\ sia vero per il caso \(i\);
• \(e\) è una costante matematica di circa 2.72;
• \(b_0\) è una costante stimata dai dati;
• \(b_1\) è un coefficiente b stimato dai dati;
• \(X_i\) è il punteggio osservato sulla variabile \(X\) per il caso \(i\).

L’essenza stessa della regressione logistica è stimare \(b_0\) e \(b_1\). Questi 2 numeri ci permettono di calcolare la probabilità che un cliente muoia data qualsiasi età osservata. Illustreremo questo con alcune curve di esempio che abbiamo aggiunto al precedente grafico a dispersione.

Curve di esempio di regressione logistica

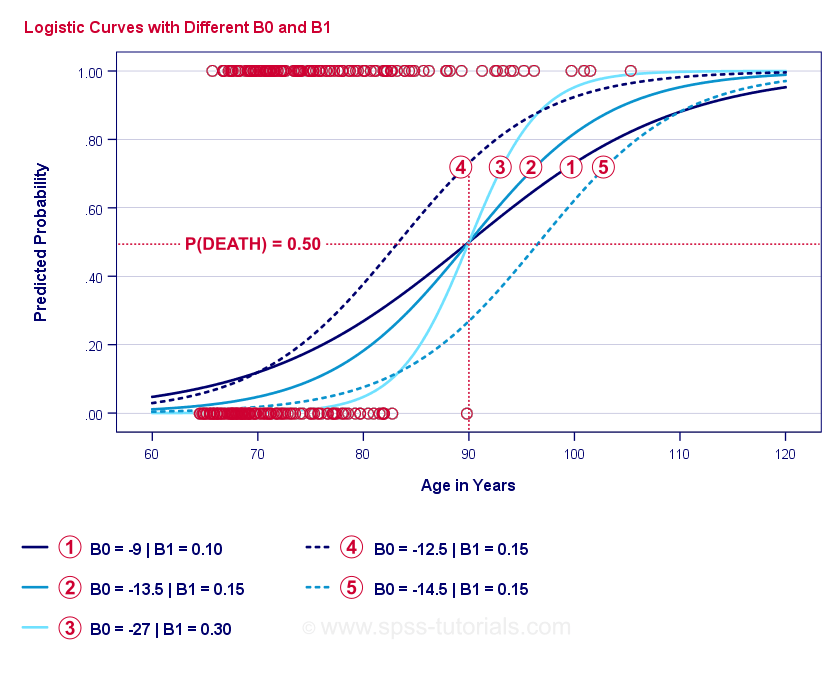
Se vi prendete un minuto per confrontare queste curve, potete vedere quanto segue:

• \(b_0\) determina la posizione orizzontale delle curve: come \(b_0\) aumenta, le curve si spostano verso sinistra ma la loro ripidità non è influenzata. Questo si vede per le curve , e . Si noti che \(b_0\) è diverso ma \(b_1\) è uguale per queste curve.
• Come aumenta \(b_0\), anche le probabilità previste aumentano: data l’età = 90 anni, la curva prevede una probabilità di morire di circa 0,75. Le curve e predicono approssimativamente 0,50 e 0,25 probabilità di morire per un cliente di 90 anni.
• \(b_1\) determina la ripidità delle curve: se \(b_1\) > 0, la probabilità di morire aumenta all’aumentare dell’età. Questa relazione diventa più forte quando \(b_1\) diventa più grande. Le curve , e illustrano questo punto: se \(b_1\) diventa più grande, le curve diventano più ripide e la probabilità di morire aumenta più velocemente con l’aumentare dell’età.

Per ora, ci rimane una domanda: come troviamo i “migliori” \(b_0\) e \(b_1\)?

Regressione logistica – Log Likelihood

Per ogni intervistato, un modello di regressione logistica stima la probabilità che qualche evento \(Y_i\) si sia verificato. Ovviamente, queste probabilità dovrebbero essere alte se l’evento si è effettivamente verificato e viceversa. Un modo per riassumere quanto bene si comporta un modello per tutti gli intervistati è la log-likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

dove

• \(Y_i\) è 1 se l’evento si è verificato e 0 se non si è verificato;
• \(ln\) indica il logaritmo naturale: a quale potenza bisogna elevare \(e\) per ottenere un dato numero?

\(LL\) è una misura di bontà dell’adattamento: a parità di condizioni, un modello di regressione logistica si adatta meglio ai dati nella misura in cui \(LL\) è più grande. Un po’ confusamente, \(LL\) è sempre negativo. Quindi vogliamo trovare i \(b_0\) e \(b_1\) per i quali
\(LL\) è il più vicino a zero possibile.

Stima della massima verosimiglianza

Al contrario della regressione lineare, la regressione logistica non può calcolare facilmente i valori ottimali per \(b_0\) e \(b_1\). Invece, abbiamo bisogno di provare diversi numeri fino a quando \(LL\) non aumenta ulteriormente. Ogni tentativo di questo tipo è noto come un’iterazione. Il processo di trovare valori ottimali attraverso tali iterazioni è noto come stima di massima verosimiglianza.

Quindi questo è fondamentalmente il modo in cui i software statistici -come SPSS, Stata o SAS- ottengono risultati di regressione logistica. Fortunatamente, sono incredibilmente bravi a farlo. Ma invece di riportare \(LL\), questi pacchetti riportano \(-2LL\).\(-2LL\) è una misura di “badness-of-fit” che segue una distribuzione
chi-quadrato.Questo rende \(-2LL\) utile per confrontare diversi modelli come vedremo tra poco. \(-2LL\) è indicato come -2 Log likelihood nell’output mostrato qui sotto.

La nota qui ci dice che la stima di massima verosimiglianza ha avuto bisogno solo di 5 iterazioni per trovare i coefficienti b ottimali \(b_0\) e \(b_1\). Quindi diamo un’occhiata a questi ora.

Regressione logistica – Coefficienti B

I risultati più importanti per qualsiasi analisi di regressione logistica sono i coefficienti b. La figura qui sotto li mostra per i nostri dati di esempio.

Prima di entrare nei dettagli, questo output mostra brevemente

i b-coefficienti che compongono il nostro modello;
gli errori standard per questi b-coefficienti;
la statistica di Wald – calcolata come \((\frac{B}{SE})^2\)- che segue una distribuzione chi-quadrato;
i gradi di libertà per la statistica Wald;
i livelli di significatività per i coefficienti b;
i coefficienti b esponenziati o \(e^B\) sono gli odds ratio associati ai cambiamenti nei punteggi predittori;
l’intervallo di confidenza al 95% per i coefficienti b esponenziati.

I coefficienti b completano il nostro modello di regressione logistica, che ora è

$$P(death_i) = \frac{1}{1 + e^{\9,079\\,+\,0.124\, \cdot\, age_i)}$$

Per un cliente di 75 anni, la probabilità di morire entro 5 anni è

$$P(morte_i) = \frac{1}{1 + e^{{{\city,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}=$$

$P(morte_i) = \frac{1}{1 + e^{\\,-\,0.249}}=$

$P(morte_i) = \frac{1}{1 + 0.780}=$$

$$P(death_i) \approx 0.562$$

Così ora sappiamo come prevedere la morte entro 5 anni data l’età di qualcuno. Ma quanto è buona questa previsione? Ci sono diversi approcci. Cominciamo con il confronto dei modelli.

Regressione logistica – Modello base

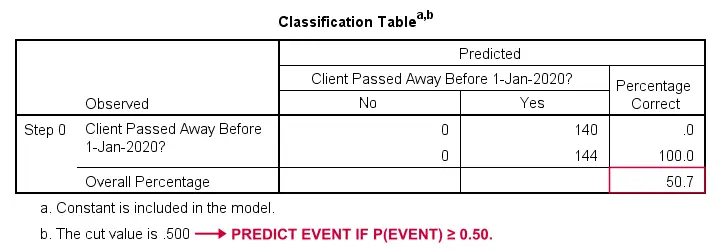
Come potremmo predire chi è morto se non avessimo altre informazioni? Beh, il 50,7% del nostro campione è morto. Quindi la probabilità prevista sarebbe semplicemente 0,507 per tutti.

Ai fini della classificazione, di solito prevediamo che un evento si verifica se p(evento) ≥ 0,50. Poiché p(è morto) = 0,507 per tutti, prevediamo semplicemente che tutti sono morti. Questa previsione è corretta per il 50,7% del nostro campione che è morto.

Regressione logistica – Rapporto di verosimiglianza

Ora, da queste probabilità previste e dai risultati osservati possiamo calcolare la nostra misura di badness-of-fit: -2LL = 393,65. Il nostro modello reale -prevedendo la morte per età- arriva a -2LL = 354,20. La differenza tra questi numeri è nota come rapporto di verosimiglianza \(LR\):

$$LR = (-2LL_{baseline}) – (-2LL_{modello})$$

Importante, \(LR\) segue una distribuzione chi-quadrato con \(df\) gradi di libertà, calcolata come

$$df = k_{modello} – k_{base}$$

dove \(k\) indica il numero di parametri stimati dai modelli. Come mostrato in questo Googlesheet, \(LR\) e \(df\) risultano in un livello di significatività per l’intero modello.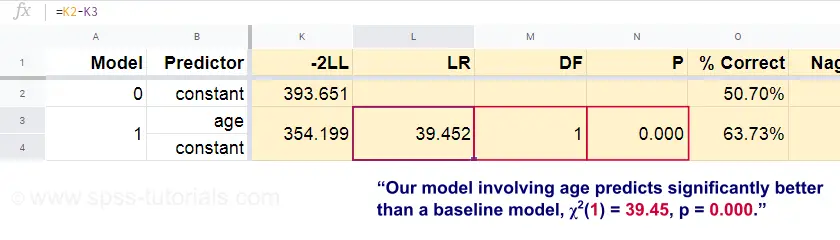

L’ipotesi nulla qui è che qualche modello predice altrettanto male del modello di base in qualche popolazione. Poiché p = 0,000, la rifiutiamo: il nostro modello (che predice la morte in base all’età) funziona significativamente meglio di un modello di base senza predittori.
Ma esattamente quanto meglio? Questa risposta è data dalla sua dimensione dell’effetto.

Regressione logistica – Dimensione dell’effetto del modello

Un buon modo per valutare quanto bene il nostro modello funzioni è da una misura di dimensione dell’effetto. Un’opzione è il Cox & Snell R2 o \(R^2_{CS}\ calcolato come

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{modello})\,-\,(-2LL_{baseline})}{n}}$

Purtroppo, \(R^2_{CS}\) non raggiunge mai il suo massimo teorico di 1. Pertanto, una versione aggiustata nota come R2 di Nagelkerke o \(R^2_{N}}} è spesso preferita:

$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}$

Per il nostro esempio di dati, \(R^2_{CS}\ = 0,130 che indica un effetto di media grandezza. \(R^2_{N}}} = 0,173, leggermente più grande della media.

Infine, \(R^2_{CS}}) e \(R^2_{N}}) sono tecnicamente completamente diversi dal quadrato r calcolato nella regressione lineare. Tuttavia, tentano di adempiere allo stesso ruolo. Entrambe le misure sono quindi conosciute come pseudo misure di r-quadro.

Regressione logistica – Dimensione dell’effetto dei predittori

Oddirittura, pochissimi libri di testo menzionano qualsiasi dimensione dell’effetto per i singoli predittori. Forse perché queste sono completamente assenti in SPSS. La ragione per cui ne abbiamo bisogno è che i coefficienti b dipendono dalle scale (arbitrarie) dei nostri predittori: se inserissimo l’età in giorni invece che in anni, il suo coefficiente b si ridurrebbe enormemente. Questo ovviamente rende i coefficienti b inadatti a confrontare i predittori all’interno o tra diversi modelli.
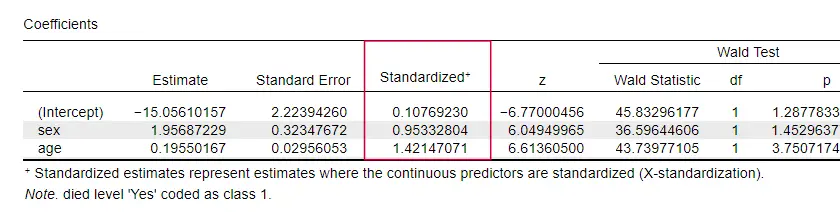
JASP include coefficienti b parzialmente standardizzati: i predittori quantitativi -ma non la variabile di risultato- sono inseriti come punteggi z come mostrato di seguito.

Assunzioni della regressione logistica

L’analisi della regressione logistica richiede le seguenti assunzioni:

1. osservazioni indipendenti;
2. specifiche corrette del modello;
3. misura senza errori della variabile risultato e di tutti i predittori;
4. linearità: ogni predittore è legato linearmente a \(e^B\) (l’odds ratio).

L’ipotesi 4 è alquanto discutibile e omessa da molti libri di testo1,6. Può essere valutata con il test Box-Tidwell come discusso da Field4. Questo fondamentalmente si riduce a testare se c’è qualche effetto di interazione tra ogni predittore e il suo logaritmo naturale o \(LN\).

Regressione logistica multipla

Finora, la nostra discussione si è limitata alla regressione logistica semplice che usa un solo predittore. Il modello è facilmente estendibile con predittori aggiuntivi, risultando in una regressione logistica multipla:

$$P(Y_i) = \frac{1}{1 + e^{\0,-\,(b_0,+\,b_1X_{1i}+\,b_2X_{2i}+\,…+\,b_kX_{ki})}$$

dove

• \(P(Y_i)\) è la probabilità prevista che \(Y\) sia vero per il caso \(i\);
• \(e\) è una costante matematica di circa 2.72;
• \(b_0\) è una costante stimata dai dati;
• \(b_1\), \(b_2\), … ,\(b_k\) sono i coefficienti b per i predittori 1, 2, … ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}}) sono i punteggi osservati sui predittori \(X_1\), \(X_2\), … ,\(X_k\) per il caso \(i\).

La regressione logistica multipla spesso comporta la selezione del modello e il controllo della multicollinearità. A parte questo, è un’estensione abbastanza diretta della regressione logistica semplice.

Questa introduzione di base si è limitata agli elementi essenziali della regressione logistica. Se vuoi saperne di più, potresti voler leggere alcuni degli argomenti che abbiamo omesso:

1. gli odds ratio -calcolati come \(e^B\) nella regressione logistica- esprimono come le probabilità cambiano a seconda dei punteggi dei predittori ;
2. il test Box-Tidwell esamina se le relazioni tra i suddetti odds ratio e i punteggi dei predittori sono lineari;
3. il test di Hosmer e Lemeshow è un test alternativo di goodness-of-fit per un intero modello di regressione logistica.

Grazie per la lettura!

1. Warner, R.M. (2013). Statistica applicata (2a edizione). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistica. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Analisi multivariata dei dati. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Scoprire la statistica con IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Metodi statistici per la psicologia (5° ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.