We beginnen de studie van partiële differentiaalvergelijkingen met het probleem van de warmtestroom in een uniforme staaf met lengte \(L), gelegen op de as \(x) met een uiteinde op de oorsprong en het andere op \(x = L\) (figuur \(PaginaIndex{1})).
We nemen aan dat de staaf perfect geïsoleerd is, behalve mogelijk aan de eindpunten, en dat de temperatuur op elke doorsnede constant is en dus alleen afhangt van \(x) en \(t). We nemen ook aan dat de thermische eigenschappen van de staaf onafhankelijk zijn van \(x) en \(t). In dit geval kan worden aangetoond dat de temperatuur u = u(x, t)op tijdstip u op een punt x eenheden van de oorsprong voldoet aan de partiële differentiaalvergelijking
waarbij u een positieve constante is die bepaald wordt door de thermische eigenschappen. Dit is de warmtevergelijking.
Om ⅓(u) te bepalen, moeten we de temperatuur in elk punt van de staaf bepalen wanneer ⅓(t=0), zeg
Dit noemen we de beginvoorwaarde. We moeten ook de randvoorwaarden bepalen waaraan u moet voldoen aan de uiteinden van de staaf voor alle punten in de staaf waar t >0> is. We noemen dit probleem een begin-grenswaarde probleem.
We beginnen met de randvoorwaarden u(0,t)=u(L,t)=0\), en schrijven het begin-grenswaarde probleem als
Onze methode om dit probleem op te lossen heet scheiding van variabelen (niet te verwarren met de methode van scheiding van variabelen die in Paragraaf 2.2 wordt gebruikt voor het oplossen van gewone differentiaalvergelijkingen). We beginnen met het zoeken naar functies van de vorm
die niet identiek nul zijn en voldoen aan
voor alle ((x,t)\). Aangezien
(v_t=a^2v_{xx}) als en slechts als
wat we herschrijven als
Aangezien de uitdrukking links onafhankelijk is van \(x,t) en de uitdrukking rechts onafhankelijk van \(t), kan deze vergelijking alleen opgaan voor alle x(x,t) als de twee zijden gelijk zijn aan dezelfde constante, die we scheidingsconstante noemen, en schrijven als x(-lambda); dus
Dit is equivalent met
en
Omdat \(v(0,t)=X(0)T(t)=0) en \(v(L,t)=X(L)T(t)=0) en we willen niet dat \(T)identiek nul is, zijn \(X(0)=0) en \(X(L)=0). Daarom moet (\lambda) een eigenwaarde zijn van het randwaardeprobleem
en \(X) moet een \(\lambda)-eigenfunctie zijn. Uit stelling 11.1.2 zijn de eigenwaarden van vergelijking \ref{eq:12.1.3} \(\lambda_n=n^2pi^2/L^2), met bijbehorende eigenfuncties
Substitutie van \(\lambda=n^2pi^2/L^2) in vergelijking \ref{eq:12.1.2} levert
.2} geeft
die de oplossing
heeftNu laat
Aangezien
(v_n) voldoet aan Vergelijking \ref{eq:12.1.1} met \(f(x)=(sin n)npi x/L\). Meer in het algemeen geldt dat als (u_m) constanten zijn en
dan voldoet (u_m) aan Vergelijking \ref{eq:12.1.1} met
Dit motiveert de volgende definitie.
Stelling
De formele oplossing van het begin-grenswaardeprobleem
is
waar
de Fourier sinusreeks is van f(f) op f(f); dat wil zeggen,
Wij gebruiken de term “formele oplossing” in deze definitie omdat het in het algemeen niet waar is dat de oneindige reeks in Vergelijking \ref{eq:12.1.5} ook werkelijk voldoet aan alle eisen van het begin-grenswaardeprobleem Vergelijking 12.1.4} wanneer dat wel het geval is, zeggen we dat het een feitelijke oplossing is van Vergelijking 12.1.4}.1.4}.
Omwille van de negatieve exponentiëlen in vergelijking \ref{eq:12.1.5} convergeert \(u) voor alle \((x,t)\) met \(t>0) (Oefening 12.1.54). Omdat elke term in vergelijking \ref{eq:12.1.5} voldoet aan de warmtevergelijking en de randvoorwaarden in vergelijking \ref{eq:12.1.4}, heeft \(u_t) ook deze eigenschappen als \(u_{xx}}) en \(u_{xx}}) kunnen worden verkregen door de reeksen in Vergelijking \ref{eq:12.1.5} term voor term te differentiëren eenmaal ten opzichte van \(t\) en tweemaal ten opzichte van \(x\), voor \(t>0}. Het is echter niet altijd legitiem om een oneindige reeks term voor term te differentiëren. De volgende stelling geeft een nuttige voldoende voorwaarde voor de legitimiteit van term-voor-term differentiatie van een oneindige reeks. Wij laten het bewijs achterwege.
De stelling
Een convergente oneindige reeks
kan term voor term gedifferentieerd worden term voor term op een gesloten interval om
te verkrijgen waarbij de afgeleiden op z=z_1) en z=z_2) eenzijdig zijn.eenzijdig zijn, op voorwaarde dat w_n continu is op w_n en waar m_1,\) \(M_2,\) …, \(M_n,\) …, constanten zijn zodat de reeks \(\sum_{n=1}^infty M_n\) convergeert.
De stelling \(\PageIndex{2}}), tweemaal toegepast met \(z=x) en eenmaal met \(z=t), toont aan dat \(u_{xx}) en \(u_t) verkregen kunnen worden door \(u) term voor term te differentiëren als \(t>0) (Oefening 12.1.54). Daarom voldoet \(u) aan de warmtevergelijking en de randvoorwaarden in Vergelijking \ref{eq:12.1.4} voor \(t>0). Omdat u(x,0)=S(x)²) voor \(0xxxxxxxxxxxxxxxxx), is u(xxxxxx) een eigenlijke oplossing van vergelijking \ref{eq:12.1.4} als en slechts als u(S(x)=f(x)²) voor \(0xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx). Uit Stelling 11.3.2 volgt dat dit waar is als \(f)continue en stukgewijs glad is op \, en \(f(0)=f(L)=0\).
In dit hoofdstuk zullen we formele oplossingen van verschillende soorten problemen definiëren. Als we je vragen zulke problemen op te lossen, bedoelen we altijd dat je een formele oplossing moet vinden.
Voorbeeld \(\PageIndex{1})
Vergelijking \ref{eq:12.1.4} oplossen met \(f(x)=x(x^2-3Lx+2L^2)\).
Oplossing
Uit voorbeeld) is
Daarom
Als beide uiteinden van staaf geïsoleerd zijn zodat er geen warmte doorheen kan, dan zijn de randvoorwaarden
We laten het aan u over (Oefening 12.1.1) om met behulp van de methode van de scheiding van variabelen en Stelling 11.1.3 de volgende definitie te motiveren.
Stelling
De formele oplossing van het begin-grenswaarde probleem
waar
de Fourier cosinus reeks van \(f\) op \(;
Voorbeeld (\PageIndex{2})
Oplos Vergelijking \ref{eq:12.1.6} met f(x)=x.
Oplossing
Uit voorbeeld 11.3.1 volgt dat de Fourier cosinusreeks van \(f) op \(\) is
Daarom
Wij laten het aan u over (oefening 12.1.2) om met behulp van de methode van de scheiding van variabelen en Stelling 11.1.4 de volgende definitie te motiveren.
De formele oplossing van het begin-grenswaardeprobleem
is
waar
de gemengde Fourier sinusreeks van \(f\) op \(;
Voorbeeld (\PageIndex{3})
Oplos Vergelijking \ref{eq:12.1.7} met f(x)=x).
Oplossing
Van voorbeeld 11.3.4 is de gemengde Fourier sinusreeks van f op x
Daaruit volgt
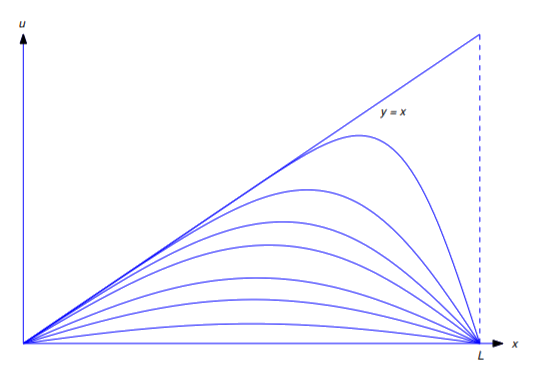
Figuur \(\PageIndex{2}) toont een grafiek van u=u(x,t)uitgezet ten opzichte van x voor verschillende waarden van t. De lijn \(y=x) komt overeen met \(t=0). De andere krommen komen overeen met positieve waarden van \(t). Als \(t) toeneemt, naderen de grafieken de lijn \(u=0}.
We laten het aan u over (Oefening 12.1.3) om met behulp van de methode van de scheiding van variabelen en Stelling 11.1.5 de volgende definitie te motiveren.
Stelling
De formele oplossing van het begin-randwaardeprobleem
is
waar
de gemengde Fourier cosinusreeks van f(f) op f(\) is; dat wil zeggen,
Voorbeeld (\PageIndex{4})
Oplos Vergelijking \ref{eq:12.1.8} met \(f(x)=x-L\).
Oplossing
Van Voorbeeld 11.3.3 is de gemengde Fourier cosinusreeks van f(x)op f(x)
Daaruit volgt
Techniek gebruiken
Numerieke experimenten kunnen uw begrip van de oplossingen van initiële-grenswaardeproblemen vergroten. Beschouw om precies te zijn de formele oplossing
van vergelijking \ref{eq:12.1.4}, waarin
de Fourier sinusreeks van \(f) op \(\) is. Beschouw de u_m(x,t)-deelsom
Voor verschillende vaste waarden van u_m(x,t)\) (waaronder u_m(t=0)), grafiek u_m(x,t)\) versus u_m(t)\). In sommige gevallen kan het nuttig zijn om de krommen die corresponderen met de verschillende waarden van \(t) op dezelfde assen te zetten, in andere gevallen kunt u de verschillende krommen achtereenvolgens (voor toenemende waarden van \(t)) in een grafiek zetten, en een primitief bewegend beeld op uw monitor maken. Herhaal dit experiment voor verschillende waarden van \(m), om te vergelijken hoe de resultaten afhangen van \(m) voor kleine en grote waarden van \(t). Bedenk wel dat de betekenis van “klein” en “groot” in dit geval afhangt van de constanten a2 en L2. Een goede manier om hiermee om te gaan is om vergelijking
te herschrijven als
waar
en een grafiek te maken van \(u_m) versus \(x) voor geselecteerde waarden van \(\tau).
Deze opmerkingen gelden ook voor de situaties die in de stellingen \(\PageIndex{3})-(\PageIndex{5}) worden beschouwd, behalve dat Vergelijking \ref{eq:12.1.13} moet worden vervangen door
in de stellingen \(\PageIndex{4})- en \(\PageIndex{5}}).