• Logistic Regression Equation
• Logistic Regression Example Curves
• Logistic Regression – B-Coefficiënten
• Logistische regressie – Effectgrootte
• Logistische regressie Veronderstellingen

Logistische regressie is een techniek om een
dichotome uitkomstvariabele te voorspellen uit 1+ voorspellers.Voorbeeld: hoe groot is de kans dat mensen voor 2020 overlijden, gegeven hun leeftijd in 2015? Merk op dat “sterven” een dichotome variabele is omdat er slechts twee mogelijke uitkomsten zijn (ja of nee).
Deze analyse staat ook bekend als binaire logistische regressie of gewoon “logistische regressie”. Een verwante techniek is multinomiale logistische regressie, die uitkomstvariabelen met meer dan 3 categorieën voorspelt.

Logistische regressie – eenvoudig voorbeeld

Een verpleeghuis heeft gegevens over het geslacht van N = 284 cliënten, hun leeftijd op 1 januari 2015 en of de cliënt vóór 1 januari 2020 is overleden. De ruwe gegevens staan in dit Googlesheet, deels hieronder weergegeven.

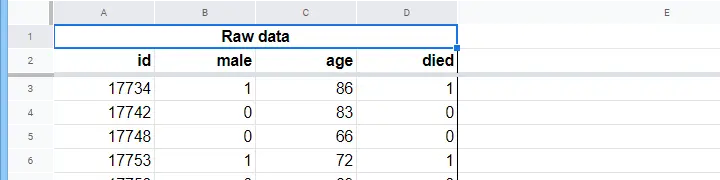
Laten we ons eerst beperken tot de leeftijd: kunnen we op basis van de leeftijd in 2015 het overlijden vóór 2020 voorspellen? En zo ja, hoe precies? En in welke mate? Een goede eerste stap is het inspecteren van een scatterplot zoals hieronder.

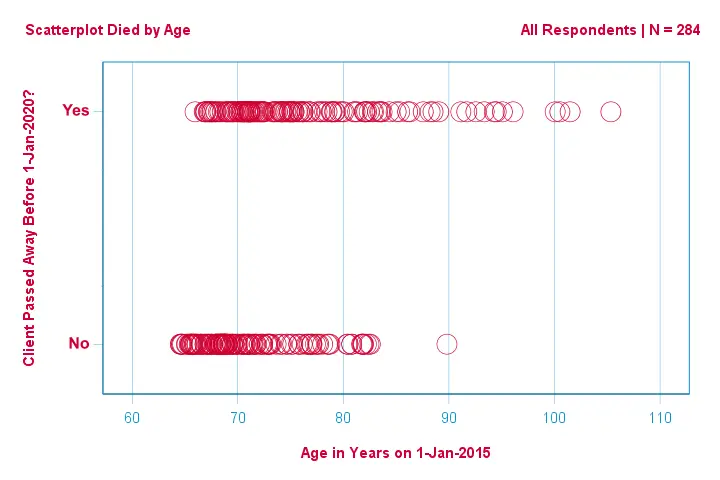
Een paar dingen die we zien in deze scatterplot zijn dat

• alle cliënten ouder dan 83 jaar op één na binnen de komende 5 jaar zijn overleden;
• de standaardafwijking van leeftijd is veel groter voor cliënten die zijn overleden dan voor cliënten die hebben overleefd;
• leeftijd heeft een aanzienlijke positieve skewness, vooral voor de cliënten die zijn overleden.

Maar hoe kunnen we voorspellen of een cliënt is overleden, gegeven zijn leeftijd? Dat doen we door een logistische curve te passen.

Eenvoudige logistische regressievergelijking

Eenvoudige logistische regressie berekent de waarschijnlijkheid van een bepaalde uitkomst gegeven een enkele voorspellende variabele als

$$P(Y_i) = \frac{1}{1 + e^{,-(b_0,+,b_1X_{1i})}}$$

waar

• (P(Y_i)\) de voorspelde kans is dat \(Y_i) waar is voor geval \(i});
• (e) is een wiskundige constante van ruwweg 2.72;
• (b_0) is een uit de gegevens geschatte constante;
• (b_1) is een uit de gegevens geschatte b-coëfficiënt;
• (X_i) is de waargenomen score op variabele \(X) voor geval \(i).

De essentie van logistische regressie is het schatten van \(b_0) en \(b_1). Met deze twee getallen kunnen we de kans berekenen dat een cliënt overlijdt, gegeven een waargenomen leeftijd. We zullen dit illustreren met enkele voorbeeldcurven die we aan de vorige scatterplot hebben toegevoegd.

Logistische Regressie Voorbeeldkrommen

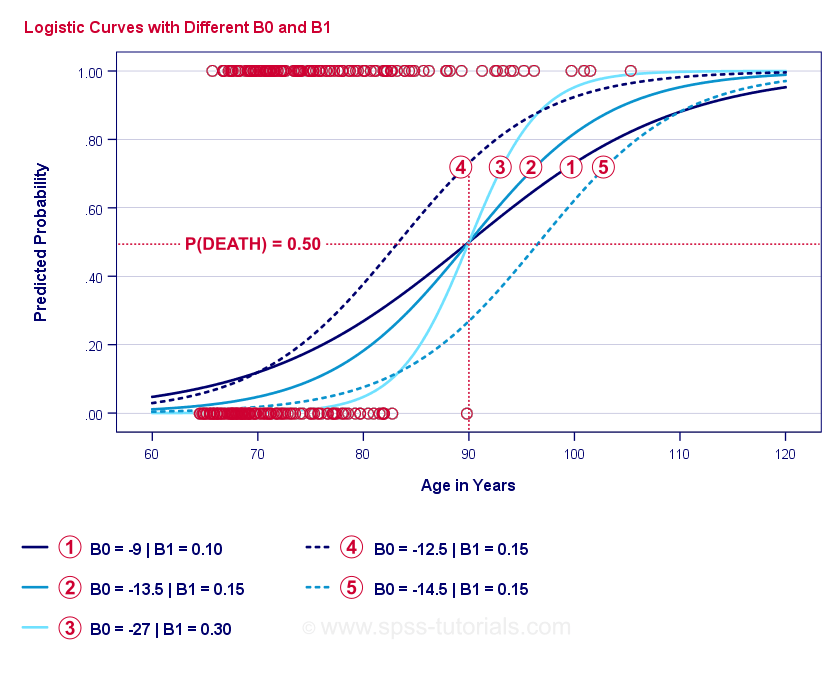
Als u even de tijd neemt om deze krommen te vergelijken, ziet u wellicht het volgende:

• \(b_0) bepaalt de horizontale positie van de krommen: naarmate \(b_0) toeneemt, verschuiven de krommen naar links, maar hun steilheid wordt niet beïnvloed. Dit is te zien voor de krommen , en . Merk op dat b0 verschillend is maar b_1 gelijk voor deze curven.
• Als \(b_0) toeneemt, nemen ook de voorspelde kansen toe: gegeven leeftijd = 90 jaar voorspelt kromme een sterftekans van ruwweg 0,75. Curven en voorspellen ruwweg 0.50 en 0.25 kans op overlijden voor een 90-jarige cliënt.
• \(b_1) bepaalt de steilheid van de curven: als \(b_1) > 0, neemt de kans op overlijden toe met toenemende leeftijd. Dit verband wordt sterker naarmate \(b_1) groter wordt. De curven , en illustreren dit: naarmate \(b_1) groter wordt, worden de curven steiler, zodat de kans om te sterven sneller toeneemt met toenemende leeftijd.

Voorlopig rest ons nog één vraag: hoe vinden we de “beste” \(b_0) en \(b_1)?

Logistische regressie – Log Waarschijnlijkheid

Voor elke respondent schat een logistisch regressiemodel de waarschijnlijkheid dat een bepaalde gebeurtenis \(Y_i) zich heeft voorgedaan. Het is duidelijk dat deze waarschijnlijkheden hoog moeten zijn als de gebeurtenis werkelijk heeft plaatsgevonden en omgekeerd. Een manier om samen te vatten hoe goed een bepaald model voor alle respondenten presteert is de logo-waarschijnlijkheid (LL):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

waar

• (Y_i) is 1 als de gebeurtenis heeft plaatsgevonden en 0 als dat niet het geval is;
• (ln) staat voor de natuurlijke logaritme: tot welke macht moet je \(e) verheffen om een bepaald getal te krijgen?

LL(LL) is een goodness-of-fit maat: als al het andere gelijk is, past een logistisch regressiemodel beter bij de gegevens naarmate LL(LL) groter is. Enigszins verwarrend, \(LL) is altijd negatief. We willen dus de waarden vinden waarvoor LL zo dicht mogelijk bij nul ligt.

Maximum Likelihood Estimation

In tegenstelling tot lineaire regressie kunnen we met logistische regressie niet zo gemakkelijk de optimale waarden voor LL berekenen. In plaats daarvan moeten we verschillende getallen proberen totdat \(LL) niet verder toeneemt. Elk van deze pogingen staat bekend als een iteratie. Het proces van het vinden van optimale waarden door middel van dergelijke iteraties staat bekend als maximum likelihood estimation.

Dat is dus in feite hoe statistische software -zoals SPSS, Stata of SAS- logistische regressieresultaten verkrijgt. Gelukkig zijn ze daar verbazingwekkend goed in. Maar in plaats van -2LL te rapporteren, rapporteren deze pakketten -2LL. -2LL is een “badness-of-fit” maat die een kwadratische verdeling volgt. Dit maakt -2LL nuttig voor het vergelijken van verschillende modellen, zoals we straks zullen zien. \De voetnoot hier vertelt ons dat de maximale waarschijnlijkheidsschatting slechts 5 iteraties nodig had voor het vinden van de optimale b-coëfficiënten b0 en b_1. Laten we daar nu eens naar kijken.

Logistische Regressie – B-coëfficiënten

De belangrijkste output voor elke logistische regressie analyse zijn de b-coëfficiënten. De figuur hieronder toont ze voor onze voorbeeldgegevens.

Voordat we in detail treden, toont deze uitvoer in het kort

de b-coëfficiënten waaruit ons model is opgebouwd;
de standaardfouten voor deze b-coëfficiënten;
de Wald-statistiek -berekend als \((\frac{B}{SE})^2\)- die een chi-kwadraatverdeling volgt;
de vrijheidsgraden voor de Wald-statistiek;
de significantieniveaus voor de b-coëfficiënten;
geëxoneerde b-coëfficiënten of ^(e^B) zijn de odds ratio’s die zijn geassocieerd met veranderingen in voorspellerscores;
het 95%-betrouwbaarheidsinterval voor de geëxoneerde b-coëfficiënten.

De b-coëfficiënten completeren ons logistische regressiemodel, dat nu

$$P(overlijden_i) = \frac{1}{1 + e^{(-9,079,+,0.124, leeftijd_i)}}$

Voor een 75-jarige cliënt is de kans om binnen 5 jaar te overlijden

$$P(overlijden_i) = \frac{1}{1 + e^{\,-,(-9.079,+,0.124, ^{,-,75)}}=$

$P(overlijden_i) = \frac{1}{1 + e^{,-,0.249}}=$

$P(overlijden_i) = \frac{1}{1 + 0.780}=$

$$P(overlijden_i) $

Dus nu weten we hoe we de dood binnen 5 jaar kunnen voorspellen gegeven iemands leeftijd. Maar hoe goed is deze voorspelling? Er zijn verschillende benaderingen. Laten we beginnen met modelvergelijkingen.

Logistische Regressie – Baseline Model

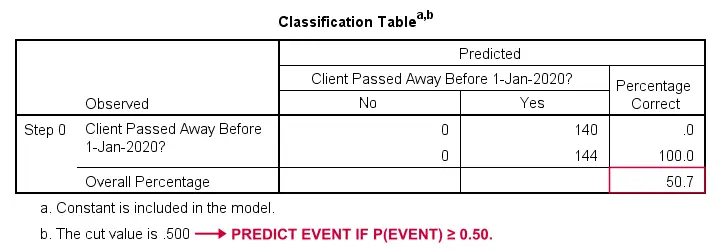
Hoe konden we voorspellen wie overleed als we geen andere informatie hadden? Wel, 50.7% van onze steekproef is overleden. Dus de voorspelde kans zou gewoon 0,507 zijn voor iedereen.

Voor classificatiedoeleinden voorspellen we meestal dat een gebeurtenis zich voordoet als p(gebeurtenis) ≥ 0,50. Aangezien p(overleden) = 0.507 voor iedereen, voorspellen we gewoon dat iedereen is overleden. Deze voorspelling is correct voor de 50,7% van onze steekproef die is overleden.

Logistische Regressie – Likelihood Ratio

Nu kunnen we uit deze voorspelde kansen en de waargenomen uitkomsten onze badness-of-fit maat berekenen: -2LL = 393.65. Ons eigenlijke model – dat sterfte door leeftijd voorspelt – komt uit op -2LL = 354.20. Het verschil tussen deze getallen staat bekend als de likelihood ratio (LR):

$$LR = (-2LL_{baseline}) – (-2LL_{model})$$

Belangrijk is dat LR een chi-kwadraat verdeling volgt met df(vrijheidsgraden), berekend als

$$df = k_{model} – k_{baseline}$$

waarbij \(k) het aantal parameters aangeeft dat door de modellen wordt geschat. Zoals uit deze Googlesheet blijkt, resulteren (LR) en (df) in een significantieniveau voor het gehele model.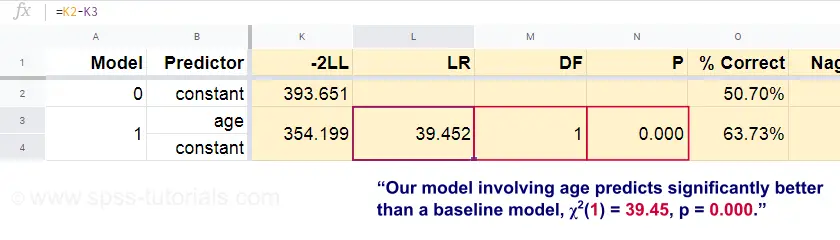

De nulhypothese hier is dat een bepaald model in een bepaalde populatie even slecht voorspelt als het basismodel. Aangezien p = 0,000, verwerpen we dit: ons model (dat de dood op basis van leeftijd voorspelt) presteert significant beter dan een basismodel zonder voorspellers.
Maar hoeveel beter precies? Dit wordt beantwoord aan de hand van de effectgrootte.

Logistische Regressie – Model Effect Grootte

Een goede manier om te beoordelen hoe goed ons model presteert, is aan de hand van een maat voor de effectgrootte. Een optie is de Cox & Snell R2 of \(R^2_{CS}} berekend als

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{model})\,-(-2LL_{baseline})}{n}}$

Helaas bereikt \(R^2_{CS}}) nooit zijn theoretische maximum van 1. Daarom wordt vaak de voorkeur gegeven aan een aangepaste versie die bekend staat als Nagelkerke R2 of \(R^2_{N}}:

$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}$

Voor onze voorbeeldgegevens is \(R^2_{CS}} = 0,130, wat wijst op een middelgrote effectgrootte. \^(R^2_{N}} = 0,173, iets groter dan middelgroot.

Ten slotte zijn ^(R^2_{CS}}) en ^(R^2_{N}}) technisch gezien totaal verschillend van r-kwadraat zoals berekend in lineaire regressie. Zij trachten echter wel dezelfde rol te vervullen. Beide maten staan daarom bekend als pseudo r-kwadraat maten.

Logistische Regressie – Voorspeller Effect Grootte

Opvallend genoeg vermelden maar heel weinig leerboeken een effectgrootte voor individuele voorspellers. Misschien komt dat omdat die in SPSS volledig ontbreken. De reden waarom we ze wel nodig hebben is dat b-coëfficiënten afhangen van de (arbitraire) schalen van onze voorspellers: als we leeftijd in dagen zouden invoeren in plaats van in jaren, zou de b-coëfficiënt enorm krimpen. Dit maakt b-coëfficiënten uiteraard ongeschikt voor het vergelijken van voorspellers binnen of tussen verschillende modellen.
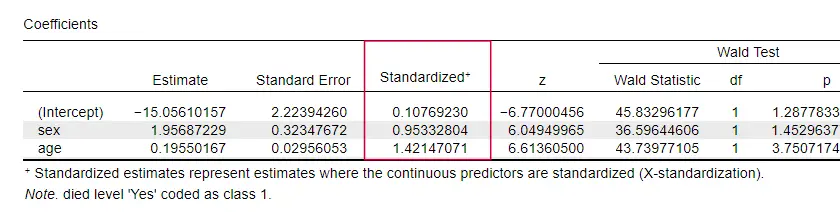
JASP bevat gedeeltelijk gestandaardiseerde b-coëfficiënten: kwantitatieve voorspellers – maar niet de uitkomstvariabele – worden ingevoerd als z-scores, zoals hieronder getoond.

Aannames voor logistische regressie

Logistische regressie-analyse vereist de volgende aannames:

1. onafhankelijke waarnemingen;
2. correcte modelspecificatie;
3. foutloze meting van uitkomstvariabele en alle voorspellers;
4. lineariteit: elke voorspeller is lineair gerelateerd aan ^(e^B\) (de odds ratio).

Aanname 4 is enigszins betwistbaar en wordt in veel leerboeken weggelaten1,6. Zij kan worden geëvalueerd met de Box-Tidwell-test, zoals besproken door Field4. Dit komt er in feite op neer dat wordt getest of er interactie-effecten zijn tussen elke voorspeller en zijn natuurlijke logaritme of LN.

Multiple Logistic Regression

Tot dusver is onze bespreking beperkt gebleven tot eenvoudige logistische regressie waarbij slechts één voorspeller wordt gebruikt. Het model is eenvoudig uit te breiden met extra voorspellers, wat resulteert in meervoudige logistische regressie:

$$P(Y_i) = \frac{1}{1 + e^{(b_0,+,b_1X_{1i}+,b_2X_{2i}+,….+\b_kX_{ki})}}$

waar

• (P(Y_i)\) de voorspelde kans is dat \(Y_i) waar is voor het geval \(i);
• (e) is een wiskundige constante van ruwweg 2.72;
• (b_0) is een constante geschat uit de gegevens;
• (b_1), \(b_2), …. zijn de b-coëfficiënten voor de voorspellers 1, 2, … ,\(k);
• (X_{1i}), \(X_{2i}), … , \(X_k}) voor geval i.

Multiple logistic regression omvat vaak modelselectie en controle op multicollineariteit. Voor de rest is het een vrij eenvoudige uitbreiding van eenvoudige logistische regressie.

Deze basisinleiding bleef beperkt tot de essentie van logistische regressie. Als u meer wilt leren, kunt u zich verder verdiepen in de onderwerpen die we hebben weggelaten:

1. odds ratio’s -berekend als ^(e^B) in logistische regressie- drukken uit hoe waarschijnlijkheden veranderen afhankelijk van voorspellerscores ;
2. de Box-Tidwell test onderzoekt of de relaties tussen de eerder genoemde odds ratio’s en voorspellerscores lineair zijn;
3. de Hosmer en Lemeshow test is een alternatieve goodness-of-fit test voor een volledig logistisch regressiemodel.

Bedankt voor het lezen!

1. Warner, R.M. (2013). Toegepaste statistiek (2e editie). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistiek. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Gegevensanalyse. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Statistiek ontdekken met IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6e. Editie). New York: Routledge.