Wir beginnen das Studium der partiellen Differentialgleichungen mit dem Problem des Wärmestroms in einem gleichförmigen Stab der Länge \(L\), der auf der Achse \(x\) liegt, wobei ein Ende im Ursprung und das andere bei \(x = L\) liegt (Abbildung \(\PageIndex{1}\)).
Wir nehmen an, dass der Stab perfekt isoliert ist, außer möglicherweise an seinen Endpunkten, und dass die Temperatur auf jedem Querschnitt konstant ist und daher nur von \(x\) und \(t\) abhängt. Wir nehmen ferner an, dass die thermischen Eigenschaften des Balkens unabhängig von \(x\) und \(t\) sind. In diesem Fall kann gezeigt werden, dass die Temperatur \(u = u(x, t)\) zum Zeitpunkt \(t\) an einem Punkt \(x\) Einheiten vom Ursprung die partielle Differentialgleichung
\
erfüllt, wobei \(a\) eine positive Konstante ist, die durch die thermischen Eigenschaften bestimmt wird. Dies ist die Wärmegleichung.
Um \(u\) zu bestimmen, müssen wir die Temperatur an jedem Punkt des Balkens angeben, wenn \(t=0\), sagen wir
\
Wir nennen dies die Anfangsbedingung. Wir müssen auch Randbedingungen angeben, die \(u\) an den Enden des Balkens für alle \(t>0\) erfüllen muss. Wir nennen dieses Problem ein Anfangs-Randwertproblem.
Wir beginnen mit den Randbedingungen \(u(0,t)=u(L,t)=0\), und schreiben das Anfangs-Randwertproblem als
\
Unsere Methode zur Lösung dieses Problems nennt man Variablentrennung (nicht zu verwechseln mit der Methode der Variablentrennung, die in Abschnitt 2.2 zur Lösung gewöhnlicher Differentialgleichungen verwendet wird). Wir beginnen mit der Suche nach Funktionen der Form
\
, die nicht identisch Null sind und
\
für alle \((x,t)\) erfüllen. Da
\
\(v_t=a^2v_{xx}\) nur dann erfüllt ist, wenn
\
, was wir umschreiben als
\
Da der Ausdruck auf der linken Seite unabhängig von \(x\) ist, während der auf der rechten Seite unabhängig von \(t\) ist, kann diese Gleichung nur dann für alle \((x,t)\) gelten, wenn die beiden Seiten gleich der gleichen Konstante sind, die wir Trennkonstante nennen und als \(-\lambda\) schreiben; also,
\
Dies ist äquivalent zu
\
und
\
Da \(v(0,t)=X(0)T(t)=0\) und \(v(L,t)=X(L)T(t)=0\) und wir nicht wollen, dass \(T\) identisch Null ist, \(X(0)=0\) und \(X(L)=0\). Daher muss \(\lambda\) ein Eigenwert des Randwertproblems
\
sein und \(X\) muss eine \(\lambda\)-Eigenfunktion sein. Aus Theorem 11.1.2 sind die Eigenwerte von Gleichung \ref{eq:12.1.3} \(\lambda_n=n^2\pi^2/L^2\), mit zugehörigen Eigenfunktionen
\
Substituiert man \(\lambda=n^2\pi^2/L^2\) in Gleichung \ref{eq:12.1.2} einsetze, ergebe
\
die die Lösung
\
habe. Nun sei
\
Da
\
\(v_n\) die Gleichung \ref{eq:12.1.1} mit \(f(x)=\sin n\pi x/L\). Allgemeiner ausgedrückt, wenn \(\alpha_1,\dots,\alpha_m\) Konstanten sind und
\
dann erfüllt \(u_m\) die Gleichung \ref{eq:12.1.1} mit
\
Das motiviert die nächste Definition.
Theorem \(\PageIndex{1}\)
Die formale Lösung des Anfangs- undRandwertproblems
\
ist
\
wobei
die Fourier-Sinusreihe von \(f\) auf \(\) ist; das heißt,
\
Wir verwenden den Begriff „formale Lösung“ in dieser Definition, weil es im Allgemeinen nicht wahr ist, dass die unendliche Reihe in Gleichung \ref{eq:12.1.5} tatsächlich alle Anforderungen des Anfangsgrenzwertproblems Gleichung \ref{eq:12.1.4} erfüllt, wenn dies der Fall ist, sagen wir, dass es sich um eine tatsächliche Lösung von Gleichung \ref{eq:12.1.4}.
Aufgrund der negativen Exponentiale in Gleichung \ref{eq:12.1.5} konvergiert \(u\) für alle \((x,t)\) mit \(t>0\) (Übung 12.1.54). Da jeder Term in Gleichung \ref{eq:12.1.5} die Wärmegleichung und die Randbedingungen in Gleichung \ref{eq:12.1.4}, so hat \(u\) ebenfalls diese Eigenschaften, wenn \(u_t\) und \(u_{xx}\) durch Differenzieren der Reihen in Gleichung \ref{eq:12.1.5} Term für Term einmal in Bezug auf \(t\) und zweimal in Bezug auf \(x\) für \(t>0\) erhalten werden können. Es ist jedoch nicht immer legitim, eine unendliche Reihe Term für Term zu differenzieren. Das folgende Theorem liefert eine nützliche hinreichende Bedingung für die Zulässigkeit der termweisen Differenzierung einer unendlichen Reihe. Wir lassen den Beweis weg.
Theorem \(\PageIndex{2}\)
Eine konvergente unendliche Reihe
\
kann differenziert werden Term für Term auf einem geschlossenen Intervall \(\) differenziert werden, um
\
\((\)zu erhalten, wobei die Ableitungen bei \(z=z_1\) und \(z=z_2\) einseitig sind\(w_n’\) einseitig sind, vorausgesetzt, dass \(w_n’\) stetig auf \(\) ist und
\
wobei \(M_1,\) \(M_2,\) …, \(M_n,\) …, Konstanten sind, so dass die Reihe \(\sum_{n=1}^\infty M_n\) konvergiert.
Der Satz \(\PageIndex{2}\), zweimal angewandt mit \(z=x\) und einmal mit \(z=t\), zeigt, dass \(u_{xx}\) und \(u_t\) durch Differenzieren von \(u\) Term für Term erhalten werden können, wenn \(t>0\) (Übung 12.1.54). Daher erfüllt \(u\) die Wärmegleichung und die Randbedingungen in Gleichung \ref{eq:12.1.4} für \(t>0\). Da \(u(x,0)=S(x)\) für \(0\le x\le L\) ist, ist \(u\) nur dann eine tatsächliche Lösung der Gleichung \ref{eq:12.1.4}, wenn \(S(x)=f(x)\) für \(0\le x\le L\). Aus Theorem 11.3.2 geht hervor, dass dies wahr ist, wenn \(f\) stetig und stückweise glatt auf \(\) ist, und \(f(0)=f(L)=0\).
In diesem Kapitel werden wir formale Lösungen für verschiedene Arten von Problemen definieren. Wenn wir Sie bitten, solche Probleme zu lösen, meinen wir immer, dass Sie eine formale Lösung finden sollen.
Beispiel \(\PageIndex{1}\)
Lösen Sie Gleichung \ref{eq:12.1.4} mit \(f(x)=x(x^2-3Lx+2L^2)\).
Lösung
Aus Beispiel \) ist
\
Daher
Wenn beide Enden des Balkens isoliert sind, so dass keine Wärme durch sie hindurchgehen kann, dann sind die Randbedingungen
\
Wir überlassen es Ihnen (Aufgabe 12.1.1), die Methode der Variablentrennung und Theorem 11.1.3 zu verwenden, um die nächste Definition zu motivieren.
Theorem \(\PageIndex{3}\)
Die formale Lösung des Anfangs-Randwertproblems
\
ist
\
wobei
\
die Fourier-Kosinusreihe von \(f\) auf \(;\), das heißt,
\
Beispiel \(\PageIndex{2}\)
Lösen Sie Gleichung \ref{eq:12.1.6} mit \(f(x)=x\).
Lösung
Aus Beispiel 11.3.1 ist die Fourier-Kosinusreihe von \(f\) auf \(\) gleich
\
Daher
\
Wir überlassen es Ihnen (Aufgabe 12.1.2), die Methode der Variablentrennung und Theorem 11.1.4 zu verwenden, um die nächste Definition zu motivieren.
Theorem \(\PageIndex{4}\)
Die formale Lösung des Anfangs-Randwertproblems
\
ist
\
wobei
\
die gemischte Fourier-Sinusreihe von \(f\) auf \(;\), das heißt,
\
Beispiel \(\PageIndex{3}\)
Lösen Sie Gleichung \ref{eq:12.1.7} mit \(f(x)=x\).
Lösung
Aus Beispiel 11.3.4 ist die gemischte Fourier-Sinusreihe von \(f\) auf \(\)
\
Daher
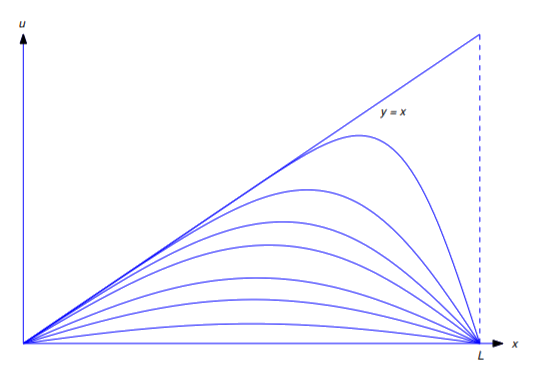
Abbildung \(\PageIndex{2}\) zeigt einen Graphen von \(u=u(x,t)\) aufgetragen in Bezug auf \(x\) für verschiedene Werte von \(t\). Die Linie \(y=x\) entspricht dem Wert \(t=0\). Die anderen Kurven entsprechen den positiven Werten von \(t\). Wenn \(t\) zunimmt, nähern sich die Graphen der Linie \(u=0\).
Wir überlassen es Ihnen (Übung 12.1.3), die Methode der Variablentrennung und den Satz 11.1.5 zu verwenden, um die nächste Definition zu motivieren.
Theorem \(\PageIndex{5}\)
Die formale Lösung des Anfangs- undRandwertproblems
\
ist
\
wobei
die gemischte Fourier-Kosinusreihe von \(f\) auf \(\) ist; das heißt,
\
Beispiel \(\PageIndex{4}\)
Lösen Sie Gleichung \ref{eq:12.1.8} mit \(f(x)=x-L\).
Lösung
Aus Beispiel 11.3.3 ist die gemischte Fourier-Kosinusreihe von \(f\) auf \(\)
\
Daher
Nutzung der Technik
Numerische Experimente können Ihr Verständnis für die Lösungen von Anfangs- und Randwertproblemen verbessern. Betrachten Sie konkret die formale Lösung
\
der Gleichung \ref{eq:12.1.4}, wobei
\
die Fourier-Sinusreihe von \(f\) auf \(\) ist. Betrachten Sie die \(m\)-te Teilsumme
\
Für mehrere feste Werte von \(t\) (einschließlich \(t=0\)), stellen Sie \(u_m(x,t)\) gegen \(t\) dar. In einigen Fällen kann es sinnvoll sein, die Kurven, die den verschiedenen Werten von \(t\) entsprechen, auf denselben Achsen darzustellen, in anderen Fällen können Sie die verschiedenen Kurven nacheinander darstellen (für steigende Werte von \(t\)) und ein primitives Bewegungsbild auf Ihrem Monitor erzeugen. Wiederholen Sie dieses Experiment für verschiedene Werte von \(m\), um zu vergleichen, wie die Ergebnisse von \(m\) für kleine und große Werte von \(t\) abhängen. Denken Sie jedoch daran, dass die Bedeutung von „klein“ und „groß“ in diesem Fall von den Konstanten \(a^2\) und \(L^2\) abhängt. Eine gute Möglichkeit, damit umzugehen, besteht darin, die Gleichung \ref{eq:12.1.12} als
\
umzuschreiben, wobei
\
und \(u_m\) gegen \(x\) für ausgewählte Werte von \(\tau\) grafisch darzustellen.
Diese Bemerkungen gelten auch für die in den Theoremen \(\PageIndex{3}\)-\(\PageIndex{5}\) betrachteten Situationen, mit der Ausnahme, dass Gleichung \ref{eq:12.1.13} in den Theoremen \(\PageIndex{4}\) und \(\PageIndex{5}\) durch
\
ersetzt werden sollte.