Einführung

Der Entscheidungsbaum ist eine Art überwachter Lernalgorithmus, der sowohl bei Regressions- als auch bei Klassifizierungsproblemen verwendet werden kann. Er funktioniert sowohl für kategorische als auch für kontinuierliche Eingangs- und Ausgangsvariablen.

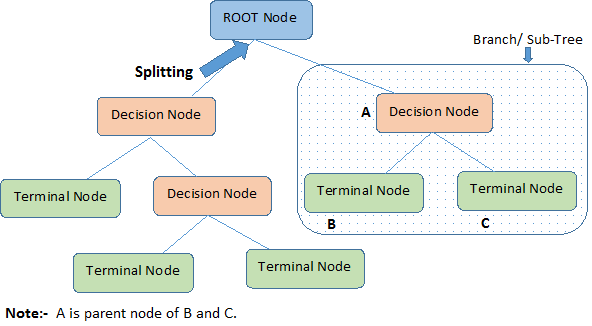
Lassen Sie uns wichtige Begriffe zum Entscheidungsbaum identifizieren, indem wir die obige Abbildung betrachten:

• Der Wurzelknoten repräsentiert die gesamte Population oder Stichprobe. Er wird weiter in zwei oder mehr homogene Gruppen unterteilt.

• Splitting ist ein Prozess, bei dem ein Knoten in zwei oder mehr Unterknoten aufgeteilt wird.

• Wenn ein Unterknoten in weitere Unterknoten aufgeteilt wird, nennt man ihn einen Entscheidungsknoten.

• Knoten, die sich nicht aufspalten, nennt man Endknoten oder Blatt.

• Wenn man Unterknoten eines Entscheidungsknotens entfernt, nennt man diesen Vorgang Pruning. Das Gegenteil von Pruning ist Splitting.

• Ein Teilbereich eines ganzen Baumes wird Branch genannt.

• Ein Knoten, der in Unterknoten aufgeteilt ist, wird als Elternknoten der Unterknoten bezeichnet, während die Unterknoten als Kind des Elternknotens bezeichnet werden.

Typen von Entscheidungsbäumen

Regressionsbäume

Schauen wir uns das folgende Bild an, das die Art der Aufteilung durch einen Regressionsbaum veranschaulicht. Es zeigt einen nicht beschnittenen Baum und einen Regressionsbaum, der an einen zufälligen Datensatz angepasst wurde. Beide Darstellungen zeigen eine Reihe von Aufteilungsregeln, beginnend an der Spitze des Baums. Beachten Sie, dass jede Aufteilung des Bereichs an einer der Merkmalsachsen ausgerichtet ist. Das Konzept der achsenparallelen Aufteilung lässt sich problemlos auf Dimensionen größer als zwei verallgemeinern. Für einen Merkmalsraum der Größe $p$, einer Teilmenge von $\mathbb{R}^p$, wird der Raum in $M$ Regionen, $R_{m}$, unterteilt, von denen jede ein $p$-dimensionaler „Hyperblock“ ist.

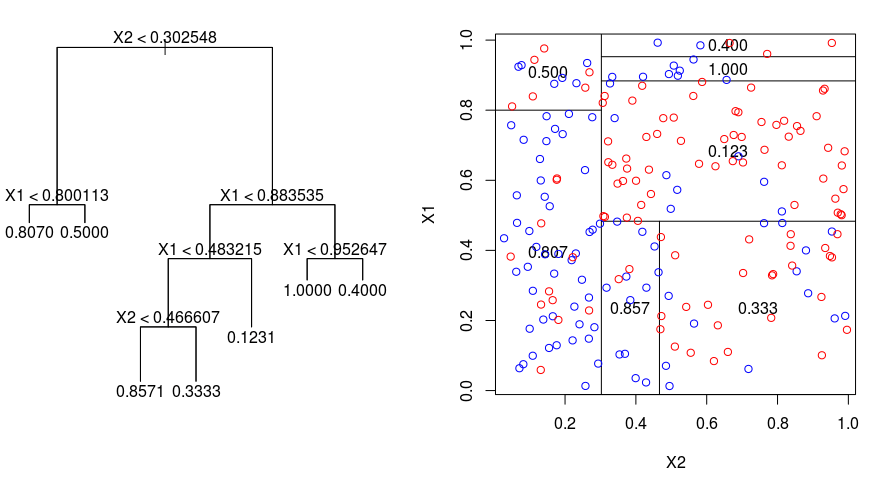
Um einen Regressionsbaum zu erstellen, verwendet man zunächst das rekursive binäre Splitting, um einen großen Baum auf den Trainingsdaten wachsen zu lassen, wobei man erst anhält, wenn jeder Endknoten weniger als eine Mindestanzahl von Beobachtungen hat. Das rekursive binäre Splitting ist ein gieriger Top-Down-Algorithmus zur Minimierung der Residual Sum of Squares (RSS), einem Fehlermaß, das auch in linearen Regressionseinstellungen verwendet wird. Die RSS ist im Falle eines partitionierten Merkmalsraums mit M Partitionen wie folgt gegeben:

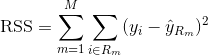
Anfangend an der Spitze des Baums wird dieser in zwei Zweige aufgeteilt, wodurch eine Partition von zwei Räumen entsteht. Man führt dann diese spezielle Aufteilung an der Spitze des Baumes mehrmals durch und wählt die Aufteilung der Merkmale, die die (aktuelle) RSS minimiert.

Nächstens wendet man Kostenkomplexitätsbeschneidung auf den großen Baum an, um eine Folge von besten Teilbäumen als Funktion von $\alpha$ zu erhalten. Die Grundidee hierbei ist die Einführung eines zusätzlichen Abstimmungsparameters, bezeichnet mit $\alpha$, der die Tiefe des Baums und seine Anpassungsfähigkeit an die Trainingsdaten ausgleicht.

Man kann K-fache Kreuzvalidierung verwenden, um $\alpha$ auszuwählen. Diese Technik besteht einfach darin, die Trainingsbeobachtungen in K Falten zu unterteilen, um die Testfehlerrate der Teilbäume zu schätzen. Ihr Ziel ist es, denjenigen auszuwählen, der zur niedrigsten Fehlerrate führt.

Klassifikationsbäume

Ein Klassifikationsbaum ist einem Regressionsbaum sehr ähnlich, außer dass er zur Vorhersage einer qualitativen Antwort anstelle einer quantitativen Antwort verwendet wird.

Erinnern Sie sich daran, dass bei einem Regressionsbaum die vorhergesagte Antwort für eine Beobachtung durch die mittlere Antwort der Trainingsbeobachtungen gegeben ist, die zu demselben Endknoten gehören. Im Gegensatz dazu wird bei einem Klassifikationsbaum vorhergesagt, dass jede Beobachtung zu der am häufigsten vorkommenden Klasse von Trainingsbeobachtungen in der Region gehört, zu der sie gehört.

Bei der Interpretation der Ergebnisse eines Klassifikationsbaums ist man oft nicht nur an der Klassenvorhersage interessiert, die einer bestimmten Endknotenregion entspricht, sondern auch an den Klassenanteilen unter den Trainingsbeobachtungen, die in diese Region fallen.

Die Aufgabe, einen Klassifikationsbaum wachsen zu lassen, ist der Aufgabe, einen Regressionsbaum wachsen zu lassen, sehr ähnlich. Genau wie bei der Regression wird ein Klassifikationsbaum durch rekursives binäres Splitting aufgebaut. Bei der Klassifizierung kann die Residualsumme der Quadrate jedoch nicht als Kriterium für die binäre Aufteilung verwendet werden. Stattdessen können Sie eine der folgenden 3 Methoden verwenden:

• Klassifikationsfehlerrate: Anstatt zu sehen, wie weit eine numerische Antwort vom Mittelwert entfernt ist, wie in der Regressionseinstellung, können Sie stattdessen die „Trefferquote“ als den Anteil der Trainingsbeobachtungen in einer bestimmten Region definieren, die nicht zu der am häufigsten vorkommenden Klasse gehören. Der Fehler wird durch diese Gleichung gegeben:

E = 1 – argmaxc($\hat{\pi}_{mc}$)

wobei $\hat{\pi}_{mc}$ den Anteil der Trainingsdaten in der Region Rm darstellt, die zur Klasse c gehören.

• Gini Index: Der Gini-Index ist eine alternative Fehlermetrik, die zeigen soll, wie „rein“ eine Region ist. „Reinheit“ bedeutet in diesem Fall, wie viel der Trainingsdaten in einer bestimmten Region zu einer einzigen Klasse gehören. Wenn eine Region Rm Daten enthält, die größtenteils zu einer einzigen Klasse c gehören, ist der Wert des Gini-Index klein:

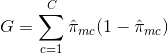
• Kreuzentropie: Eine dritte Alternative, die dem Gini-Index ähnlich ist, wird als Kreuz-Entropie oder Abweichung bezeichnet:

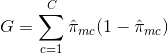
Die Kreuz-Entropie nimmt einen Wert nahe Null an, wenn die $\hat{\pi}_{mc}$-Werte alle nahe 0 oder nahe 1 sind. Wie der Gini-Index nimmt also auch die Kreuzentropie einen kleinen Wert an, wenn der m-te Knoten rein ist. Es stellt sich heraus, dass der Gini-Index und die Kreuzentropie numerisch recht ähnlich sind.

Bei der Erstellung eines Klassifikationsbaums werden in der Regel entweder der Gini-Index oder die Kreuzentropie verwendet, um die Qualität eines bestimmten Splits zu bewerten, da sie empfindlicher auf die Knotenreinheit reagieren als die Klassifikationsfehlerrate. Jeder dieser drei Ansätze kann beim Beschneiden des Baums verwendet werden, aber die Klassifizierungsfehlerrate ist vorzuziehen, wenn die Vorhersagegenauigkeit des endgültigen beschnittenen Baums das Ziel ist.

Vor- und Nachteile von Entscheidungsbäumen

Der Hauptvorteil der Verwendung von Entscheidungsbäumen ist, dass sie intuitiv sehr einfach zu erklären sind. Im Vergleich zu anderen Regressions- und Klassifikationsansätzen spiegeln sie die menschliche Entscheidungsfindung sehr gut wider. Sie lassen sich grafisch darstellen und können problemlos mit qualitativen Prädiktoren umgehen, ohne dass Dummy-Variablen erstellt werden müssen.

Entscheidungsbäume haben jedoch im Allgemeinen nicht den gleichen Grad an Vorhersagegenauigkeit wie andere Ansätze, da sie nicht sehr robust sind. Eine kleine Änderung in den Daten kann zu einer großen Änderung im endgültigen geschätzten Baum führen.

Durch die Aggregation vieler Entscheidungsbäume unter Verwendung von Methoden wie Bagging, Random Forests und Boosting kann die Vorhersageleistung von Entscheidungsbäumen erheblich verbessert werden.

Baumbasierte Methoden

Bagging

Die oben besprochenen Entscheidungsbäume leiden unter einer hohen Varianz, d.h. wenn man die Trainingsdaten nach dem Zufallsprinzip in zwei Teile aufteilt und einen Entscheidungsbaum an beide Hälften anpasst, können die Ergebnisse, die man erhält, sehr unterschiedlich sein. Im Gegensatz dazu liefert ein Verfahren mit geringer Varianz ähnliche Ergebnisse, wenn es wiederholt auf unterschiedliche Datensätze angewandt wird.

Bagging oder Bootstrap-Aggregation ist eine Technik, die zur Verringerung der Varianz Ihrer Vorhersagen verwendet wird, indem die Ergebnisse mehrerer Klassifikatoren kombiniert werden, die auf verschiedenen Unterproben desselben Datensatzes modelliert wurden. Hier die Gleichung für Bagging:

Dabei werden $B$ verschiedene Bootstrap-Trainingsdatensätze erzeugt. Dann trainieren Sie Ihre Methode auf dem $b-ten$ Bootstrap-Trainingsdatensatz, um $\hat{f}_{b}(x)$ zu erhalten, und schließlich bilden Sie den Durchschnitt der Vorhersagen.

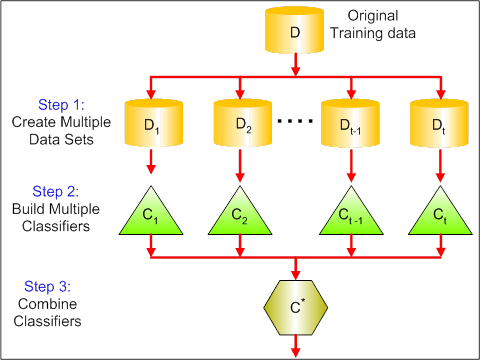
Die folgende Abbildung zeigt die 3 verschiedenen Schritte des Bagging:

• Schritt 1: Hier ersetzen Sie die ursprünglichen Daten durch neue Daten. Die neuen Daten haben in der Regel einen Bruchteil der Spalten und Zeilen der ursprünglichen Daten, die dann als Hyperparameter im Bagging-Modell verwendet werden können.

• Schritt 2: Sie erstellen Klassifikatoren auf jedem Datensatz. Im Allgemeinen können Sie denselben Klassifikator für die Erstellung von Modellen und Vorhersagen verwenden.

• Schritt 3: Schließlich verwenden Sie einen Durchschnittswert, um die Vorhersagen aller Klassifikatoren zu kombinieren, je nach Problemstellung. Im Allgemeinen sind diese kombinierten Werte robuster als ein einzelnes Modell.

Während Bagging die Vorhersagen für viele Regressions- und Klassifizierungsmethoden verbessern kann, ist es besonders nützlich für Entscheidungsbäume. Um Bagging auf Regressions-/Klassifikationsbäume anzuwenden, konstruiert man einfach $B$ Regressions-/Klassifikationsbäume unter Verwendung von $B$ Bootstrap-Trainingsmengen und mittelt die resultierenden Vorhersagen. Diese Bäume sind tief gewachsen und werden nicht beschnitten. Daher hat jeder einzelne Baum eine hohe Varianz, aber eine geringe Verzerrung. Durch die Mittelung dieser $B$-Bäume wird die Varianz reduziert.

Gemeinsam betrachtet hat sich gezeigt, dass Bagging zu beeindruckenden Verbesserungen der Genauigkeit führt, indem Hunderte oder sogar Tausende von Bäumen in einem einzigen Verfahren kombiniert werden.

Random Forests

Random Forests ist eine vielseitige maschinelle Lernmethode, die sowohl Regressions- als auch Klassifizierungsaufgaben durchführen kann. Es führt auch Methoden zur Dimensionsreduktion durch, behandelt fehlende Werte, Ausreißerwerte und andere wesentliche Schritte der Datenexploration und leistet recht gute Arbeit.

Random Forests bietet eine Verbesserung gegenüber Bagging-Bäumen durch eine kleine Änderung, die die Bäume dekoriert. Wie beim Bagging erstellt man eine Reihe von Entscheidungsbäumen auf Basis von Bootstrap-Trainingsstichproben. Bei der Erstellung dieser Entscheidungsbäume wird jedoch jedes Mal, wenn ein Split in einem Baum in Betracht gezogen wird, eine Zufallsstichprobe von m Prädiktoren als Split-Kandidaten aus dem vollständigen Satz von $p$ Prädiktoren ausgewählt. Der Split darf nur einen dieser $m$ Prädiktoren verwenden. Dies ist der Hauptunterschied zwischen Random Forests und Bagging; denn wie beim Bagging ist die Auswahl der Prädiktoren $m = p$.

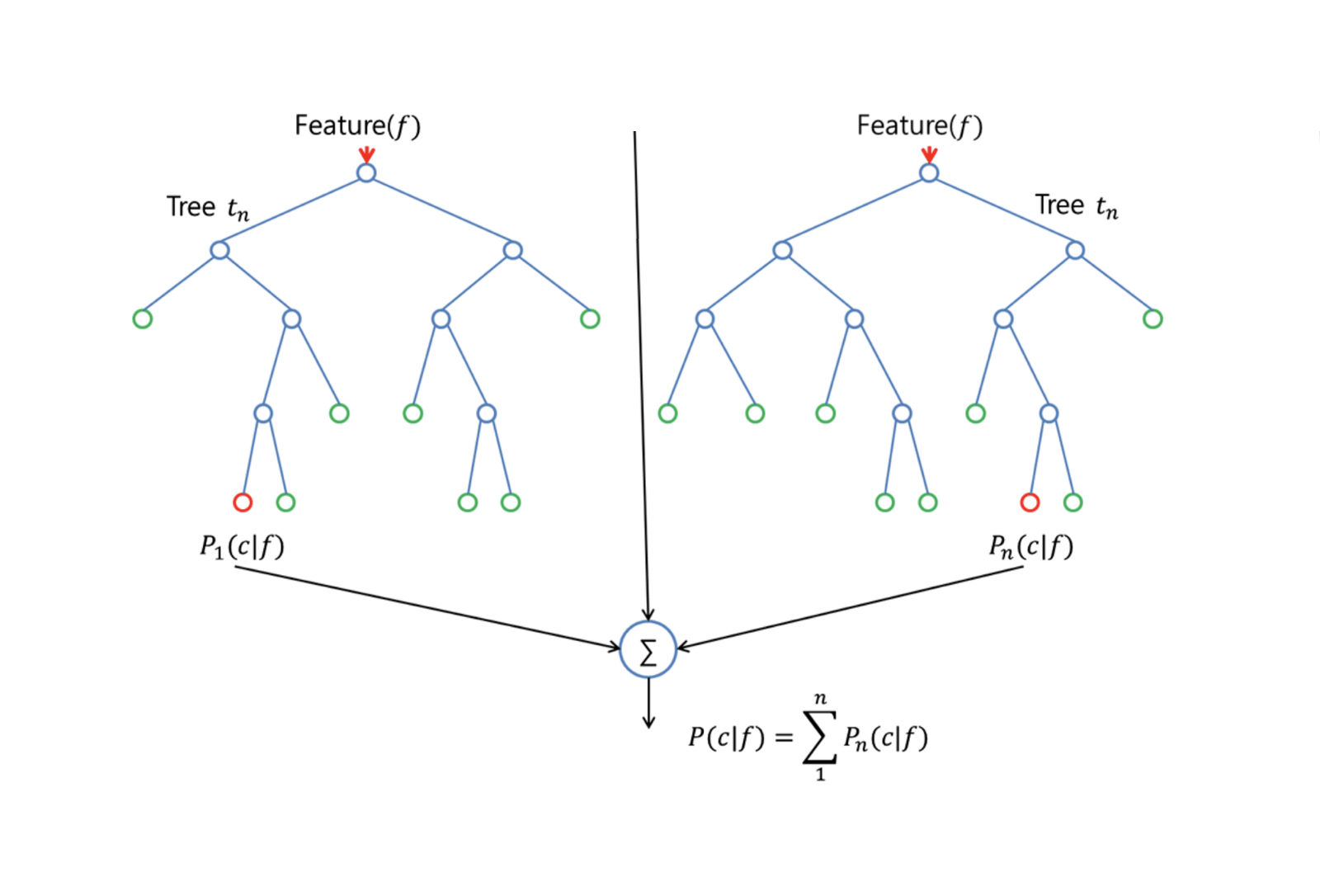
Um einen Random Forest zu erzeugen, sollte man:

• Zunächst nimmt man an, dass die Anzahl der Fälle in der Trainingsmenge K ist. Nehmen Sie dann eine Zufallsstichprobe aus diesen K Fällen und verwenden Sie diese Stichprobe als Trainingsmenge für das Wachsen des Baums.

• Wenn es $p$ Eingabevariablen gibt, geben Sie eine Zahl $m < p$ an, so dass Sie an jedem Knoten $m$ Zufallsvariablen aus den $p$ auswählen können. Die beste Aufteilung dieser $m$ wird verwendet, um den Knoten aufzuteilen.

• Jeder Baum wird anschließend so weit wie möglich vergrößert, und es ist kein Pruning erforderlich.

• Schließlich werden die Vorhersagen der Zielbäume aggregiert, um neue Daten vorherzusagen.

Random Forests ist sehr effektiv bei der Schätzung fehlender Daten und der Aufrechterhaltung der Genauigkeit, wenn ein großer Anteil der Daten fehlt. Er kann auch Fehler in Datensätzen ausgleichen, in denen die Klassen unausgewogen sind. Am wichtigsten ist jedoch, dass er große Datensätze mit hoher Dimensionalität verarbeiten kann. Ein Nachteil der Verwendung von Random Forests besteht jedoch darin, dass verrauschte Datensätze leicht überangepasst werden können, insbesondere bei der Regression.

Boosting

Boosting ist ein weiterer Ansatz zur Verbesserung der Vorhersagen, die sich aus einem Entscheidungsbaum ergeben. Wie Bagging und Random Forests ist es ein allgemeiner Ansatz, der auf viele statistische Lernmethoden zur Regression oder Klassifizierung angewendet werden kann. Erinnern Sie sich daran, dass beim Bagging mehrere Kopien des ursprünglichen Trainingsdatensatzes mithilfe des Bootstraps erstellt werden, ein separater Entscheidungsbaum an jede Kopie angepasst wird und dann alle Bäume kombiniert werden, um ein einziges Vorhersagemodell zu erstellen. Jeder Baum wird auf einem Bootstrap-Datensatz erstellt, unabhängig von den anderen Bäumen.

Boosting funktioniert auf ähnliche Weise, nur dass die Bäume nacheinander erstellt werden: Jeder Baum wird anhand der Informationen der zuvor erstellten Bäume erstellt. Beim Boosting werden keine Bootstrap-Stichproben gezogen; stattdessen wird jeder Baum an eine modifizierte Version des Originaldatensatzes angepasst.

Für Regressions- und Klassifikationsbäume funktioniert Boosting folgendermaßen:

• Im Gegensatz zur Anpassung eines einzelnen großen Entscheidungsbaums an die Daten, die auf eine harte Anpassung der Daten und eine potenzielle Überanpassung hinausläuft, lernt der Boosting-Ansatz stattdessen langsam.

• Ausgehend von dem aktuellen Modell wird ein Entscheidungsbaum an die Residuen des Modells angepasst. Das heißt, man passt einen Baum an, der die aktuellen Residuen und nicht das Ergebnis $Y$ als Antwort verwendet.

• Dann fügt man diesen neuen Entscheidungsbaum in die angepasste Funktion ein, um die Residuen zu aktualisieren. Jeder dieser Bäume kann recht klein sein, mit nur wenigen Endknoten, die durch den Parameter $d$ im Algorithmus bestimmt werden. Indem man kleine Bäume an die Residuen anpasst, verbessert man $\hat{f}$ langsam in Bereichen, in denen es nicht gut funktioniert.

• Der Schrumpfungsparameter $\nu$ verlangsamt den Prozess noch weiter und erlaubt es mehr und anders geformten Bäumen, die Residuen anzugreifen.

Boosting ist sehr nützlich, wenn man eine große Datenmenge hat und erwartet, dass die Entscheidungsbäume sehr komplex sind. Boosting wurde verwendet, um viele anspruchsvolle Klassifizierungs- und Regressionsprobleme zu lösen, darunter Risikoanalyse, Stimmungsanalyse, prädiktive Werbung, Preismodellierung, Umsatzschätzung und Patientendiagnose, um nur einige zu nennen.

Entscheidungsbäume in R

Klassifizierungsbäume

Für diesen Teil arbeiten Sie mit dem Carseats-Datensatz unter Verwendung des tree-Pakets in R. Beachten Sie, dass Sie zunächst die Pakete ISLR und tree in Ihrer R Studio-Umgebung installieren müssen. Laden wir zunächst den Carseats-Datenrahmen aus dem Paket ISLR.

library(ISLR)data(package="ISLR")carseats<-Carseats

Laden wir auch das Paket tree.

require(tree)

Der Carseats-Datensatz ist ein Datenrahmen mit 400 Beobachtungen zu den folgenden 11 Variablen:

• Umsatz: Absatz in Tausend Stück

• CompPreis: Preis des Wettbewerbers an jedem Standort

• Einkommen: Einkommensniveau der Gemeinde in 1000 Dollar

• Werbung: lokales Werbebudget an jedem Standort in Tausend Dollar

• Bevölkerung: regionale Einwohnerzahl in Tausend

• Preis: Preis für Autositze an jedem Standort

• ShelveLoc: Schlecht, Gut oder Mittel gibt die Qualität des Regalstandorts an

• Alter: Altersniveau der Bevölkerung

• Bildung: Bildungsniveau am Standort

• Urban: Ja/Nein

• USA: Ja/Nein

names(carseats)

Werfen wir einen Blick auf das Histogramm der Autoverkäufe:

hist(carseats$Sales)

Beachten Sie, dass Sales eine quantitative Variable ist. Sie möchten dies anhand von Bäumen mit einer binären Antwort demonstrieren. Dazu verwandeln Sie Sales in eine binäre Variable, die High heißt. Wenn der Umsatz kleiner als 8 ist, wird er nicht hoch sein. Andernfalls wird er hoch sein. Dann können Sie diese neue Variable High wieder in den Datenrahmen einfügen.

High = ifelse(carseats$Sales<=8, "No", "Yes")carseats = data.frame(carseats, High)

Nun wollen wir ein Modell mit Entscheidungsbäumen füllen. Natürlich kann die Variable Sales hier nicht verwendet werden, da die Antwortvariable High aus Sales erstellt wurde. Schließen wir sie also aus und passen den Baum an.

tree.carseats = tree(High~.-Sales, data=carseats)

Sehen wir uns die Zusammenfassung Ihres Klassifikationsbaums an:

summary(tree.carseats)

Sie sehen die beteiligten Variablen, die Anzahl der Endknoten, die mittlere Restabweichung sowie die Fehlklassifikationsfehlerrate. Um die Sache anschaulicher zu machen, stellen wir den Baum auch grafisch dar und kommentieren ihn dann mit der praktischen Funktion text:

plot(tree.carseats)text(tree.carseats, pretty = 0)

Es gibt so viele Variablen, dass es sehr kompliziert ist, den Baum zu betrachten. Immerhin können Sie sehen, dass die Endknoten mit Yes oder No gekennzeichnet sind. An jedem Aufteilungsknoten werden die Variablen und der Wert der Aufteilungsentscheidung angezeigt (z. B. Price < 92.5 oder Advertising < 13.5).

Für eine detaillierte Zusammenfassung des Baums drucken Sie ihn einfach aus. Das ist praktisch, wenn Sie Details aus dem Baum für andere Zwecke auslesen wollen:

tree.carseats

Es ist Zeit, den Baum zu verkleinern. Wir erstellen einen Trainings- und einen Testsatz, indem wir den carseats-Datenrahmen in 250 Trainings- und 150 Testmuster aufteilen. Zunächst legen Sie einen Seed fest, um die Ergebnisse reproduzierbar zu machen. Dann nehmen Sie eine Zufallsstichprobe aus den ID-Nummern (Index) der Stichproben. In diesem Fall nehmen Sie eine Stichprobe aus der Menge 1 bis n Zeilenanzahl der Autositze, also 400. Sie wollen eine Stichprobe der Größe 250 (standardmäßig wird die Stichprobe ohne Ersetzung verwendet).

set.seed(101)train=sample(1:nrow(carseats), 250)

So erhalten Sie nun diesen Index von train, der 250 der 400 Beobachtungen indiziert. Sie können das Modell mit tree neu anpassen, indem Sie die gleiche Formel verwenden, außer dass Sie dem Baum sagen, dass er eine Teilmenge verwenden soll, die train entspricht. Erstellen wir nun ein Diagramm:

tree.carseats = tree(High~.-Sales, carseats, subset=train)plot(tree.carseats)text(tree.carseats, pretty=0)

Das Diagramm sieht aufgrund des leicht veränderten Datensatzes etwas anders aus. Dennoch sieht die Komplexität des Baumes ungefähr gleich aus.

Nun nehmen Sie diesen Baum und sagen ihn auf der Testmenge voraus, indem Sie die predict Methode für Bäume verwenden. In diesem Fall müssen Sie die class-Etiketten vorhersagen.

tree.pred = predict(tree.carseats, carseats, type="class")

Dann können Sie den Fehler mithilfe einer Fehlklassifizierungstabelle auswerten.

with(carseats, table(tree.pred, High))

Auf den Diagonalen befinden sich die korrekten Klassifizierungen, während außerhalb der Diagonalen die falschen liegen. Sie wollen nur die richtigen Klassifizierungen auswerten. Dazu kann man die Summe der beiden Diagonalen durch die Gesamtzahl (150 Testbeobachtungen) dividieren.

(72 + 43) / 150

Ok, mit diesem Baum erhält man einen Fehler von 0,76.

Bei einem großen, buschigen Baum könnte die Varianz zu groß sein. Daher sollten wir die Kreuzvalidierung verwenden, um den Baum optimal zu beschneiden. Mit cv.tree wird der Fehlklassifizierungsfehler als Grundlage für die Beschneidung verwendet.

cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)cv.carseats

Das Ausdrucken der Ergebnisse zeigt die Details des Pfades der Kreuzvalidierung. Sie können die Größe der Bäume sehen, während sie zurückgeschnitten wurden, die Abweichungen, während das Pruning fortschritt, sowie den Kostenkomplexitätsparameter, der in dem Prozess verwendet wurde.

Lassen Sie uns dies grafisch darstellen:

plot(cv.carseats)

Bei Betrachtung des Diagramms sehen Sie einen Teil der Abwärtsspirale aufgrund des Fehlklassifikationsfehlers bei 250 kreuzvalidierten Punkten. Wählen wir also einen Wert in den absteigenden Stufen (12). Dann beschneiden wir den Baum auf eine Größe von 12, um diesen Baum zu identifizieren. Schließlich wird der Baum gezeichnet und mit Anmerkungen versehen, um das Ergebnis zu sehen.

prune.carseats = prune.misclass(tree.carseats, best = 12)plot(prune.carseats)text(prune.carseats, pretty=0)

Er ist etwas flacher als die vorherigen Bäume, und man kann die Beschriftungen tatsächlich lesen. Testen wir ihn noch einmal mit dem Testdatensatz.

tree.pred = predict(prune.carseats, carseats, type="class")with(carseats, table(tree.pred, High))

(74 + 39) / 150

Sieht so aus, als ob die korrekten Klassifizierungen ein wenig gesunken sind. Der Baum hat in etwa dasselbe Ergebnis wie der ursprüngliche Baum erzielt, also hat das Beschneiden in Bezug auf die Fehlklassifizierungsfehler nicht sehr geschadet und einen einfacheren Baum ergeben.

In vielen Fällen liefern Bäume keine sehr guten Vorhersagefehler, also lassen Sie uns einen Blick auf Random Forests und Boosting werfen, die dazu neigen, Bäume in Bezug auf Vorhersage und Fehlklassifizierung zu übertreffen.

Random Forests

Für diesen Teil werden Sie die Boston housing data verwenden, um Random Forests und Boosting zu untersuchen. Der Datensatz befindet sich im MASS-Paket. Er enthält Wohnungswerte und andere Statistiken für jeden der 506 Vororte von Boston auf der Grundlage der Volkszählung von 1970.

library(MASS)data(package="MASS")boston<-Bostondim(boston)names(boston)

Laden wir auch das Paket randomForest.

require(randomForest)

Um die Daten für den Random Forest vorzubereiten, legen wir den Seed fest und erstellen einen Trainingssatz mit 300 Beobachtungen.

set.seed(101)train = sample(1:nrow(boston), 300)

In diesem Datensatz gibt es 506 Vororte von Boston. Für jeden Vorort gibt es Variablen wie Kriminalität pro Kopf, Arten von Industrie, durchschnittliche Anzahl von Zimmern pro Wohnung, durchschnittlicher Anteil des Alters der Häuser usw. Verwenden wir medv – den Medianwert der Eigenheime für jeden dieser Vororte – als Antwortvariable.

Wir passen einen Random Forest an und sehen, wie gut er abschneidet. Wie gesagt, verwenden Sie die Antwort medv, den Median des Wohnwerts (in 1.000 Dollar) und die Trainingsstichprobe.

rf.boston = randomForest(medv~., data = boston, subset = train)rf.boston

Das Ausdrucken des Random Forest liefert eine Zusammenfassung: die Anzahl der Bäume (500 wurden gezüchtet), die mittleren quadrierten Residuen (MSR) und den Prozentsatz der erklärten Varianz. Die MSR und der Prozentsatz der erklärten Varianz basieren auf den Out-of-Bag-Schätzungen, einer sehr cleveren Vorrichtung in Random Forests, um ehrliche Fehlerschätzungen zu erhalten.

Der einzige Tuning-Parameter in einem Random Forests ist das Argument mtry, das die Anzahl der Variablen angibt, die bei jedem Split eines jeden Baumes ausgewählt werden, wenn Sie einen Split machen. Wie hier zu sehen ist, entspricht mtry 4 der 13 Untersuchungsvariablen (außer medv) in den Daten von Boston Housing – was bedeutet, dass jedes Mal, wenn der Baum einen Knoten aufteilt, 4 Variablen nach dem Zufallsprinzip ausgewählt werden und die Aufteilung dann auf 1 dieser 4 Variablen beschränkt wird. Auf diese Weise randomForests werden die Bäume dekorreliert.

Sie werden eine Reihe von Random Forests anpassen. Es gibt 13 Variablen, also lassen wir mtry von 1 bis 13 reichen:

• Um die Fehler zu erfassen, richten Sie 2 Variablen oob.err und test.err ein.

• In einer Schleife von mtry von 1 bis 13 passen Sie zuerst randomForest mit diesem Wert von mtry auf den train-Datensatz an, wobei Sie die Anzahl der Bäume auf 350 beschränken.

• Dann extrahiert man den mittleren quadratischen Fehler für das Objekt (den Out-of-Bag-Fehler).

• Dann wird eine Vorhersage für den Testdatensatz (boston) unter Verwendung von fit (dem Fit von randomForest) durchgeführt.

• Schließlich wird der Testfehler berechnet: der mittlere quadratische Fehler, der mean( (medv - pred) ^ 2 ).

oob.err = double(13)test.err = double(13)for(mtry in 1:13){ fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350) oob.err = fit$mse pred = predict(fit, boston) test.err = with(boston, mean( (medv-pred)^2 ))}

Grundsätzlich haben Sie gerade 4550 Bäume (13 mal 350) gezogen. Nun wollen wir mit dem Befehl matplot ein Diagramm erstellen. Der Testfehler und der Out-of-Bag-Fehler werden zu einer zweispaltigen Matrix zusammengefügt. Es gibt noch einige andere Argumente in der Matrix, einschließlich der Werte für die Plot-Zeichen (pch = 23 bedeutet gefüllte Raute), Farben (rot und blau), Typ gleich beides (beide Punkte werden geplottet und mit den Linien verbunden) und Name der y-Achse (mittlerer quadratischer Fehler). Sie können auch eine Legende in der oberen rechten Ecke des Diagramms einfügen.

matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))

Im Grunde sollten diese beiden Kurven übereinstimmen, aber es scheint, dass der Testfehler etwas niedriger ist. Allerdings gibt es bei diesen Testfehlerschätzungen eine große Variabilität. Da die Schätzung des Out-of-Bag-Fehlers auf der Grundlage eines Datensatzes und die Schätzung des Testfehlers auf der Grundlage eines anderen Datensatzes berechnet wurde, liegen diese Unterschiede ziemlich genau innerhalb der Standardfehler.

Haben Sie bemerkt, dass die rote Kurve gleichmäßig über der blauen Kurve liegt? Diese Fehlerschätzungen sind stark korreliert, da die randomForest mit mtry = 4 der mit mtry = 5 sehr ähnlich ist. Deshalb ist jede der Kurven ziemlich glatt. Sie sehen, dass mtry mit einem Wert um 4 die optimale Wahl zu sein scheint, zumindest für den Testfehler. Dieser Wert von mtry für den Out-of-bag-Fehler ist gleich 9.

So haben Sie mit sehr wenigen Stufen ein sehr leistungsfähiges Vorhersagemodell mit Zufallswäldern erstellt. Wie kommt das? Die linke Seite zeigt die Leistung eines einzelnen Baums. Der mittlere quadratische Fehler bei Out-of-Bag beträgt 26, und Sie haben ihn auf etwa 15 gesenkt (etwas mehr als die Hälfte). Das bedeutet, dass Sie den Fehler um die Hälfte reduziert haben. Auch beim Testfehler haben Sie den Fehler von 20 auf 12 reduziert.

Boosting

Im Vergleich zu Random Forests erzeugt Boosting kleinere und robustere Bäume und geht auf den Bias ein. Sie werden das Paket GBM (Gradient Boosted Modeling) in R verwenden.

require(gbm)

GBM fragt nach der Verteilung, die Gauß ist, weil Sie den quadratischen Fehlerverlust verwenden werden. Sie werden GBM nach 10.000 Bäumen fragen, was sich nach einer Menge anhört, aber das werden flache Bäume sein. Die Interaktionstiefe ist die Anzahl der Splits, Sie wollen also 4 Splits in jedem Baum. Die Schrumpfung ist 0,01, d.h. um wie viel der Baum zurückgeschrumpft werden soll.

boost.boston = gbm(medv~., data = boston, distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)summary(boost.boston)

Die Funktion summary liefert eine Darstellung der Bedeutung der Variablen. Es scheint, dass es 2 Variablen gibt, die eine hohe relative Bedeutung haben: rm (Anzahl der Zimmer) und lstat (Prozentsatz der Menschen mit niedrigem wirtschaftlichen Status in der Gemeinde). Stellen wir diese beiden Variablen dar:

plot(boost.boston,i="lstat")plot(boost.boston,i="rm")

Das erste Diagramm zeigt, dass der Wert der Wohnungspreise umso niedriger ist, je höher der Anteil der Menschen mit niedrigerem Status in dem Vorort ist. Das zweite Diagramm zeigt die umgekehrte Beziehung zur Anzahl der Zimmer: die durchschnittliche Anzahl der Zimmer im Haus steigt mit dem Preis.

Es ist an der Zeit, ein geboostetes Modell auf dem Testdatensatz vorherzusagen. Betrachten wir die Testleistung in Abhängigkeit von der Anzahl der Bäume:

• Zunächst wird ein Raster der Anzahl der Bäume in 100er-Schritten von 100 bis 10.000 erstellt.

• Dann wird die Funktion predict auf das Boosted-Modell angewendet. Sie nimmt n.trees als Argument und erzeugt eine Matrix von Vorhersagen für die Testdaten.

• Die Dimensionen der Matrix sind 206 Testbeobachtungen und 100 verschiedene Vorhersagevektoren für die 100 verschiedenen Werte des Baums.

  n.trees = seq(from = 100, to = 10000, by = 100)predmat = predict(boost.boston, newdata = boston, n.trees = n.trees)dim(predmat)

Jetzt ist es an der Zeit, den Testfehler für jeden der Vorhersagevektoren zu berechnen:

• predmat ist eine Matrix, medv ist ein Vektor, also ist (predmat – medv) eine Matrix der Differenzen. Sie können die Funktion apply auf die Spalten dieser quadratischen Differenzen (den Mittelwert) anwenden. Das würde den spaltenweisen mittleren quadratischen Fehler für die Vorhersagevektoren berechnen.

• Dann erstellen Sie ein Diagramm mit ähnlichen Parametern wie das für Random Forest verwendete. Es würde eine Darstellung des Boosting-Fehlers zeigen.

  boost.err = with(boston, apply( (predmat - medv)^2, 2, mean) )plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")abline(h = min(test.err), col = "red")

Der Boosting-Fehler nimmt mit zunehmender Anzahl von Bäumen ziemlich stark ab. Dies ist ein Beweis dafür, dass das Boosting nur ungern eine Überanpassung vornimmt. Lassen Sie uns auch den besten Testfehler aus dem randomForest in das Diagramm aufnehmen. Boosting liegt tatsächlich ein gutes Stück unter dem Testfehler für randomForest.

Schlussfolgerung

So, das ist das Ende dieses R-Tutorials über die Erstellung von Entscheidungsbaummodellen: Klassifikationsbäume, Random Forests und Boosted Trees. Die beiden letztgenannten sind leistungsstarke Methoden, die Sie jederzeit nach Bedarf einsetzen können. Nach meiner Erfahrung ist Boosting in der Regel besser als RandomForest, aber RandomForest ist einfacher zu implementieren. Bei RandomForest ist der einzige Abstimmungsparameter die Anzahl der Bäume, während bei Boosting neben der Anzahl der Bäume noch weitere Abstimmungsparameter erforderlich sind, darunter die Schrumpfung und die Interaktionstiefe.

Wenn Sie mehr erfahren möchten, sollten Sie sich unseren Kurs Machine Learning Toolbox for R ansehen.