• Logistische Regressionsgleichung
• Logistische Regression – Beispielkurven
• Logistische Regression – Effektgröße
• Logistische Regression – B-Koeffizienten B-Koeffizienten
• Logistische Regression – Effektgröße
• Logistische Regression – Annahmen

Logistische Regression ist eine Technik zur Vorhersage einer
dichotomen Ergebnisvariable aus 1+ Prädiktoren.Beispiel: Wie wahrscheinlich ist es, dass Menschen vor 2020 sterben, wenn man ihr Alter im Jahr 2015 berücksichtigt? Beachten Sie, dass „sterben“ eine dichotome Variable ist, da es nur 2 mögliche Ergebnisse gibt (ja oder nein).
Diese Analyse ist auch als binäre logistische Regression oder einfach als „logistische Regression“ bekannt. Eine verwandte Technik ist die multinomiale logistische Regression, die Ergebnisvariablen mit 3+ Kategorien vorhersagt.

Logistische Regression – einfaches Beispiel

Ein Pflegeheim hat Daten über das Geschlecht von N = 284 Kunden, das Alter am 1. Januar 2015 und darüber, ob der Kunde vor dem 1. Januar 2020 verstorben ist. Die Rohdaten befinden sich in diesem Googlesheet, das teilweise unten abgebildet ist.

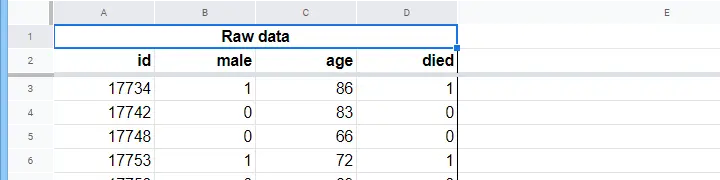
Konzentrieren wir uns zunächst nur auf das Alter: Können wir aus dem Alter im Jahr 2015 den Tod vor 2020 vorhersagen?Und – wenn ja – wie genau? Und in welchem Ausmaß? Ein guter erster Schritt ist die Inspektion eines Streudiagramms wie das unten gezeigte.

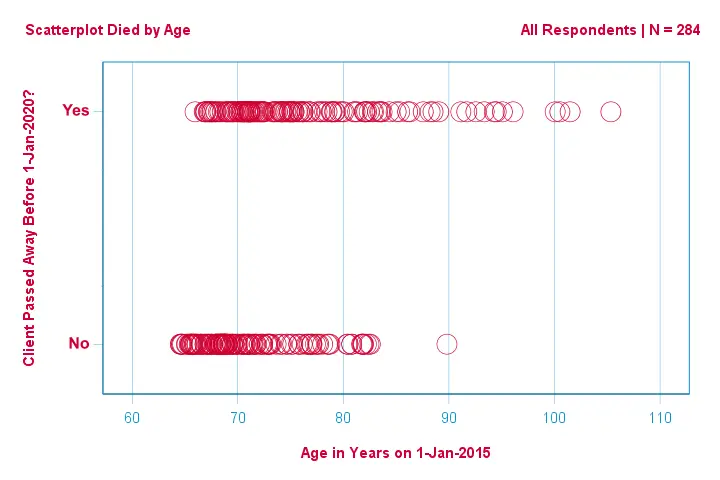
Ein paar Dinge, die wir in diesem Streudiagramm sehen, sind, dass

• alle bis auf einen Kunden, der über 83 Jahre alt war, innerhalb der nächsten 5 Jahre gestorben sind;
• die Standardabweichung des Alters ist für die Kunden, die gestorben sind, viel größer als für die Kunden, die überlebt haben;
• das Alter hat eine beträchtliche positive Schiefe, insbesondere für die Kunden, die gestorben sind.

Aber wie können wir vorhersagen, ob ein Kunde gestorben ist, wenn wir sein Alter kennen? Wir werden genau das tun, indem wir eine logistische Kurve anpassen.

Einfache logistische Regressionsgleichung

Die einfache logistische Regression berechnet die Wahrscheinlichkeit eines bestimmten Ergebnisses bei einer einzigen Vorhersagevariablen als

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}$$

wobei

• \(P(Y_i)\) die vorhergesagte Wahrscheinlichkeit ist, dass \(Y\) für den Fall \(i\) wahr ist;
• \(e\) ist eine mathematische Konstante von etwa 2.72;
• \(b_0\) ist eine aus den Daten geschätzte Konstante;
• \(b_1\) ist ein aus den Daten geschätzter b-Koeffizient;
• \(X_i\) ist der beobachtete Wert der Variable \(X\) für den Fall \(i\).

Das eigentliche Wesen der logistischen Regression ist die Schätzung von \(b_0\) und \(b_1\). Mit diesen beiden Zahlen können wir die Wahrscheinlichkeit berechnen, dass ein Kunde bei einem beliebigen beobachteten Alter stirbt. Wir werden dies anhand einiger Beispielkurven veranschaulichen, die wir dem vorherigen Streudiagramm hinzugefügt haben.

Logistische Regressions-Beispielkurven

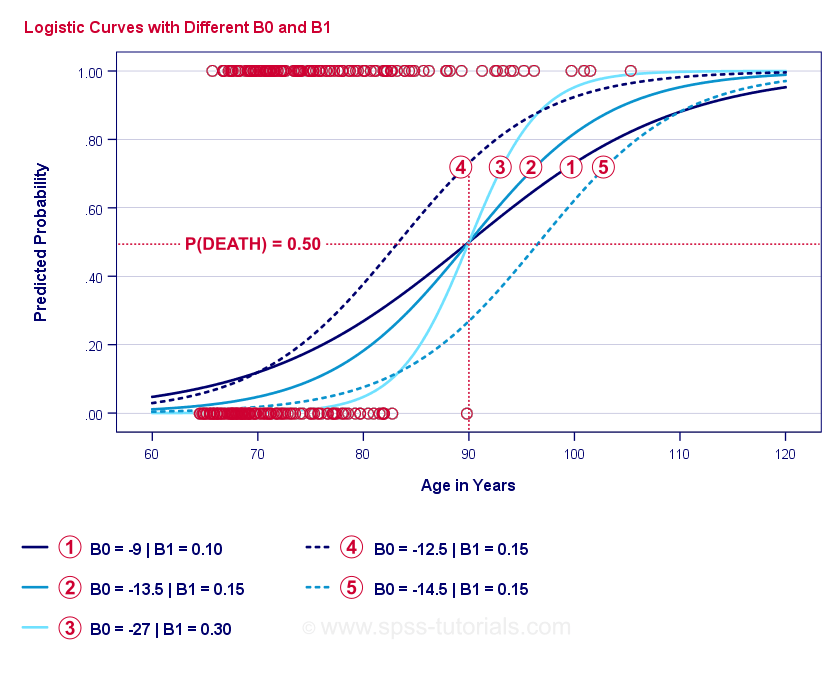
Wenn Sie sich eine Minute Zeit nehmen, um diese Kurven zu vergleichen, können Sie Folgendes feststellen:

• \(b_0\) bestimmt die horizontale Position der Kurven: Wenn \(b_0\) zunimmt, verschieben sich die Kurven nach links, aber ihre Steilheit bleibt unverändert. Dies ist für die Kurven , und zu sehen. Man beachte, dass \(b_0\) unterschiedlich ist, aber \(b_1\) für diese Kurven gleich ist.
• Mit zunehmendem \(b_0\) steigen auch die vorhergesagten Wahrscheinlichkeiten: bei einem Alter von 90 Jahren sagt die Kurve eine Wahrscheinlichkeit von etwa 0,75 voraus. Die Kurven und sagen für einen 90-jährigen Klienten eine Sterbewahrscheinlichkeit von etwa 0,50 bzw. 0,25 voraus.
• \(b_1\) bestimmt die Steilheit der Kurven: wenn \(b_1\) > 0 ist, steigt die Sterbewahrscheinlichkeit mit zunehmendem Alter. Diese Beziehung wird stärker, wenn \(b_1\) größer wird. Die Kurven , und veranschaulichen diesen Punkt: Je größer \(b_1\) wird, desto steiler werden die Kurven, so dass die Wahrscheinlichkeit, zu sterben, mit zunehmendem Alter schneller steigt.

Bleibt nur noch eine Frage: Wie finden wir die „besten“ \(b_0\) und \(b_1\)?

Logistische Regression – Log Likelihood

Für jeden Befragten schätzt ein logistisches Regressionsmodell die Wahrscheinlichkeit, dass ein bestimmtes Ereignis \(Y_i\) eingetreten ist. Natürlich sollten diese Wahrscheinlichkeiten hoch sein, wenn das Ereignis tatsächlich eingetreten ist und umgekehrt. Eine Möglichkeit, die Leistung eines Modells für alle Befragten zusammenzufassen, ist die Log-Likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 – Y_i) \cdot ln(1 – P(Y_i))$$

wobei

• \(Y_i\) 1 ist, wenn das Ereignis eingetreten ist, und 0, wenn es nicht eingetreten ist;
• \(ln\) bezeichnet den natürlichen Logarithmus: um welche Potenz muss man \(e\) erhöhen, um eine bestimmte Zahl zu erhalten?

\(LL\) ist ein Maß für die Anpassungsgüte: Bei sonst gleichen Bedingungen passt ein logistisches Regressionsmodell besser zu den Daten, je größer \(LL\) ist. Etwas verwirrend ist, dass \(LL\) immer negativ ist. Wir wollen also die \(b_0\) und \(b_1\) finden, für die
\(LL\) so nahe wie möglich bei Null liegt.

Maximum-Likelihood-Schätzung

Im Gegensatz zur linearen Regression können bei der logistischen Regression die optimalen Werte für \(b_0\) und \(b_1\) nicht ohne weiteres berechnet werden. Stattdessen müssen wir verschiedene Zahlen ausprobieren, bis \(LL\) nicht mehr ansteigt. Jeder dieser Versuche wird als Iteration bezeichnet. Der Prozess der Ermittlung optimaler Werte durch solche Iterationen wird als Maximum-Likelihood-Schätzung bezeichnet.

So erhalten also statistische Programme wie SPSS, Stata oder SAS logistische Regressionsergebnisse. Glücklicherweise sind sie erstaunlich gut darin. Aber anstatt \(LL\) anzugeben, geben diese Pakete \(-2LL\) an. \(-2LL\) ist ein Maß für die Anpassungsgüte, das einer
Chi-Quadrat-Verteilung folgt. \(-2LL\) ist daher nützlich für den Vergleich verschiedener Modelle, wie wir gleich sehen werden. \(-2LL\) wird in der unten gezeigten Ausgabe als -2 Log Likelihood bezeichnet.

Die Fußnote hier besagt, dass die Maximum-Likelihood-Schätzung nur 5 Iterationen benötigt, um die optimalen b-Koeffizienten \(b_0\) und \(b_1\) zu finden.

Logistische Regression – B-Koeffizienten

Das wichtigste Ergebnis jeder logistischen Regressionsanalyse sind die B-Koeffizienten. Die folgende Abbildung zeigt sie für unsere Beispieldaten.

Bevor wir ins Detail gehen, zeigt diese Ausgabe kurz

die b-Koeffizienten, aus denen unser Modell besteht;
die Standardfehler für diese b-Koeffizienten;
die Wald-Statistik – berechnet als \((\frac{B}{SE})^2\) – die einer Chi-Quadrat-Verteilung folgt;
die Freiheitsgrade für die Wald-Statistik;
die Signifikanzniveaus für die b-Koeffizienten;
exponentiierte b-Koeffizienten oder \(e^B\) sind die Odds Ratios, die mit Änderungen der Prädiktorwerte verbunden sind;
das 95%-Konfidenzintervall für die exponentiierten b-Koeffizienten.

Die b-Koeffizienten vervollständigen unser logistisches Regressionsmodell, das nun

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124, \cdot\, age_i)}}$$

Für einen 75-jährigen Kunden ist die Wahrscheinlichkeit, innerhalb von 5 Jahren zu versterben

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}=$$

$$P(Tod_i) = \frac{1}{1 + e^{\,-\,0.249}}=$$

$$P(Tod_i) = \frac{1}{1 + 0.780}=$$

$$P(death_i) \approx 0.562$$$

So, jetzt wissen wir, wie man den Tod innerhalb von 5 Jahren vorhersagen kann, wenn man das Alter von jemandem kennt. Aber wie gut ist diese Vorhersage? Es gibt mehrere Ansätze. Beginnen wir mit Modellvergleichen

Logistische Regression – Basismodell

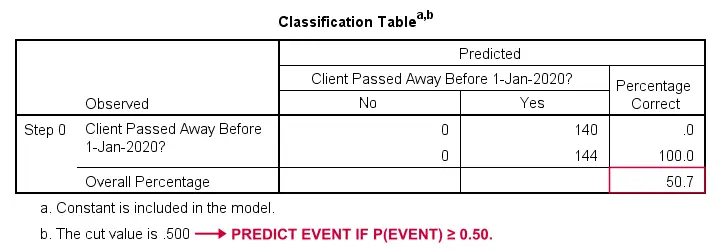
Wie könnten wir vorhersagen, wer verstorben ist, wenn wir keine anderen Informationen hätten? Nun, 50,7 % unserer Stichprobe sind verstorben. Die vorhergesagte Wahrscheinlichkeit wäre also einfach 0,507 für alle.

Zu Klassifizierungszwecken sagen wir normalerweise voraus, dass ein Ereignis eintritt, wenn p(Ereignis) ≥ 0,50 ist. Da p(gestorben) = 0,507 für alle ist, sagen wir einfach voraus, dass alle verstorben sind. Diese Vorhersage ist korrekt für die 50,7 % unserer Stichprobe, die gestorben sind.

Logistische Regression – Likelihood Ratio

Aus diesen vorhergesagten Wahrscheinlichkeiten und den beobachteten Ergebnissen können wir nun unser Maß für die Passgenauigkeit berechnen: -2LL = 393,65. Unser tatsächliches Modell, das den Tod aufgrund des Alters vorhersagt, ergibt -2LL = 354,20. Die Differenz zwischen diesen Zahlen wird als Likelihood Ratio \(LR\) bezeichnet:

$$LR = (-2LL_{Basislinie}) – (-2LL_{Modell})$$

Wichtig ist, dass \(LR\) einer Chi-Quadrat-Verteilung mit \(df\) Freiheitsgraden folgt, berechnet als

$$df = k_{Modell} – k_{Basislinie}$$

wobei \(k\) die Anzahl der von den Modellen geschätzten Parameter bezeichnet. Wie in diesem Googlesheet dargestellt, ergeben \(LR\) und \(df\) ein Signifikanzniveau für das gesamte Modell.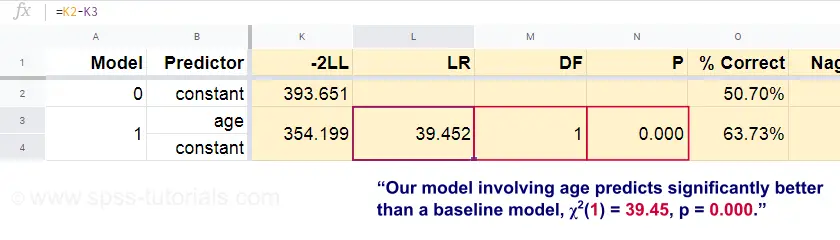

Die Nullhypothese lautet hier, dass ein bestimmtes Modell in einer bestimmten Population ebenso schlechte Vorhersagen macht wie das Basismodell. Da p = 0,000 ist, lehnen wir dies ab: Unser Modell (das den Tod aufgrund des Alters vorhersagt) schneidet signifikant besser ab als ein Basismodell ohne Prädiktoren.
Aber wie viel besser genau? Dies wird durch die Effektgröße beantwortet.

Logistische Regression – Modelleffektgröße

Eine gute Möglichkeit, die Leistung unseres Modells zu bewerten, ist die Messung der Effektgröße. Eine Möglichkeit ist das Cox & Snell R2 oder \(R^2_{CS}\), das wie folgt berechnet wird

$$R^2_{CS} = 1 – e^{\frac{(-2LL_{Modell})\,-\,(-2LL_{Basislinie})}{n}}$$

Dummerweise erreicht \(R^2_{CS}\) nie sein theoretisches Maximum von 1. Daher wird oft eine bereinigte Version, bekannt als Nagelkerke R2 oder \(R^2_{N}\), bevorzugt:

$$R^2_{N} = \frac{R^2_{CS}}{1 – e^{-\frac{-2LL_{baseline}}{n}}$$

Für unsere Beispieldaten ist \(R^2_{CS}\) = 0,130, was auf eine mittlere Effektgröße hinweist. \(R^2_{N}\) = 0,173, also etwas größer als mittelgroß.

Schließlich sind \(R^2_{CS}\) und \(R^2_{N}\) technisch gesehen etwas völlig anderes als r-Quadrat, wie es bei der linearen Regression berechnet wird. Sie versuchen jedoch, die gleiche Aufgabe zu erfüllen. Beide Maße werden daher als Pseudo-R-Quadratmaße bezeichnet.

Logistische Regression – Effektgröße der Prädiktoren

Auffallend ist, dass nur sehr wenige Lehrbücher die Effektgröße für einzelne Prädiktoren erwähnen. Vielleicht liegt das daran, dass sie in SPSS überhaupt nicht vorhanden sind. Der Grund, warum wir sie brauchen, ist, dass die b-Koeffizienten von den (willkürlichen) Skalen unserer Prädiktoren abhängen: Wenn wir das Alter in Tagen statt in Jahren eingeben würden, würde der b-Koeffizient enorm schrumpfen. Dies macht die b-Koeffizienten offensichtlich ungeeignet für den Vergleich von Prädiktoren innerhalb oder zwischen verschiedenen Modellen.
JASP enthält teilweise standardisierte b-Koeffizienten: quantitative Prädiktoren – aber nicht die Ergebnisvariable – werden als z-Scores eingegeben, wie unten gezeigt.

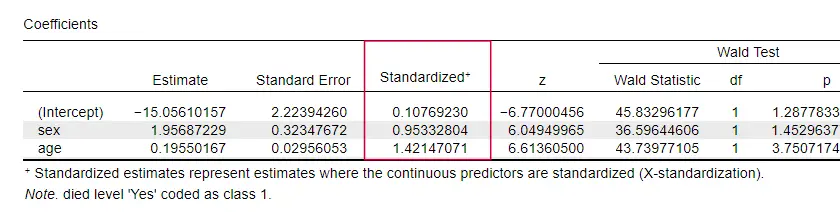
Annahmen der logistischen Regression

Die logistische Regressionsanalyse erfordert die folgenden Annahmen:

1. unabhängige Beobachtungen;
2. korrekte Modellspezifikation;
3. fehlerfreie Messung der Ergebnisvariablen und aller Prädiktoren;
4. Linearität: jeder Prädiktor steht in linearer Beziehung zu \(e^B\) (dem Odds Ratio).

Annahme 4 ist etwas umstritten und wird in vielen Lehrbüchern nicht berücksichtigt1,6. Sie kann mit dem Box-Tidwell-Test bewertet werden, wie er von Field4 diskutiert wird. Dabei wird im Wesentlichen geprüft, ob es Wechselwirkungen zwischen jedem Prädiktor und seinem natürlichen Logarithmus oder \(LN\) gibt.

Mehrfache logistische Regression

Bislang beschränkte sich unsere Diskussion auf die einfache logistische Regression, die nur einen Prädiktor verwendet. Das Modell lässt sich leicht mit zusätzlichen Prädiktoren erweitern, was zu einer multiplen logistischen Regression führt:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,…+\,b_kX_{ki})}}$$

wobei

• \(P(Y_i)\) die vorhergesagte Wahrscheinlichkeit ist, dass \(Y\) für den Fall \(i\) wahr ist;
• \(e\) ist eine mathematische Konstante von ungefähr 2.72;
• \(b_0\) ist eine aus den Daten geschätzte Konstante;
• \(b_1\), \(b_2\), … ,\(b_k\) sind die b-Koeffizienten für die Prädiktoren 1, 2, … ,\(k\);
• \(X_{1i}\), \(X_{2i}\), … ,\(X_{ki}\) sind beobachtete Werte für die Prädiktoren \(X_1\), \(X_2\), … ,\(X_k\) für den Fall \(i\).

Multiple logistische Regression beinhaltet oft die Modellauswahl und die Überprüfung auf Multikollinearität. Ansonsten handelt es sich um eine recht unkomplizierte Erweiterung der einfachen logistischen Regression.

Diese grundlegende Einführung beschränkte sich auf die wichtigsten Aspekte der logistischen Regression. Wenn Sie mehr erfahren möchten, sollten Sie einige der Themen nachlesen, die wir ausgelassen haben:

1. Die Odds Ratios – berechnet als \(e^B\) in der logistischen Regression – drücken aus, wie sich die Wahrscheinlichkeiten in Abhängigkeit von den Prädiktorwerten ändern;
2. der Box-Tidwell-Test prüft, ob die Beziehungen zwischen den vorgenannten Odds Ratios und den Prädiktorwerten linear sind;
3. der Hosmer- und Lemeshow-Test ist ein alternativer Anpassungsgütetest für ein gesamtes logistisches Regressionsmodell.

Danke fürs Lesen!

1. Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
2. Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
3. Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Datenanalyse. New Jersey: Pearson Prentice Hall.
4. Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
5. Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
6. Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6. Auflage). New York: Routledge.