(複素数に関する「オイラーの公式」は他にもありますが、
このページは幾何学とグラフで使われるものについてです)
オイラーの公式
自分と交差しない任意の多面体について、以下のようにします。
- 面の数
- + 頂点(角)の数
- – 辺の数
は常に 2
と等しく、これはこう書くことができる。 F + V – E = 2
 |
これを立方体でやってみるのです。 立方体は6面、8頂点、12辺なので、 6 + 8 – 12 = 2 |
プラトニックソリッドでの例
5プラトニックソリッドで試してみましょう。
| 名前 | 面 | 頂点 | 端 | F+V- | F+V- | EndesE | |
|---|---|---|---|---|---|---|---|
| 四面体 |  |
4 | 6 | 2 | |||
| Cube |  |
6 | 8 | 12 | 2 | ||
| 八面体 |  |
8 | 6 | 12 | 2 | ||
正十字形面体 |
12 | 20 | 30 | 2 | |||
| 正20面体 |  |
12 | 30 | 2 |
(実はオイラーの公式は、プラトニックソリッドが5つしかないことを証明するのに使える)
|
なぜいつも2なのか? 7 + 8 – 13 = 2 |
 |
|
あるいは別の頂点を入れてみて、 6 + 9 – 13 = 2. |
 |
| 「何をしても最後は2」 (ただしこのタイプの多面体の場合のみ・・・続きを読む) |
The Sphere

すべてのプラトン立体(と他の多くの立体)は球体のようです…我々は球体になるように形を変える(その角を動かして、その表面を少し曲げる)ことができます。
このことから、球体ではF+V-E=2であることがわかります
(F+V-E=1なので、球体は面が1、頂点と辺が0と単純には言えないので注意)
つまり結果はまた2なんですね。
But Not Always 2 … !
さて、これでうまくいくことがわかったので、うまくいかないことを発見しましょう。
正20面体の対角2つを結合したらどうでしょう。
それはまだ正20面体です(しかし、もはや凸状ではありません)。
実際、誰かが上と下を縫い合わせたドラム缶のように見えます。
So:
F + V – E = 1
Oh No! 常に足して 2 にならない。
これがうまくいかない理由は、この新しい形状が基本的に異なるからです…中央の結合ビットは、2 つの頂点が 1 に減少することを意味します。
Euler Characteristic
つまり、F+V-Eは2にも1にもなり得るし、他の値もあり得るので、より一般的な式は
F + V – E = χ
ここでχは「Euler Characteristic」と呼ばれています。
ここで、いくつかの例を挙げてみましょう。
| Shape | χ | |
|---|---|---|
| 球 |  |
2 |
| Torus |  |
0 |
| Mobius Strip | 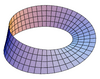 |
0 |

またオイラー特性は0より小さいこともあります。
これが “Cubohemioctahedron “です。 10 面(もっとあるように見えるかもしれませんが、「内側」の面は実際には 1 面です)、24 辺、12 頂点を持つので、
F + V – E = -2
実際、オイラー特性はトポロジー(空間の性質に関する研究)の基本概念なのです。
ドーナツとコーヒーカップ

(アニメーション提供
Wikipedia User:Kieff)
最後に、ドーナツとコーヒーカップが本当に同じであることを示さなければ、この議論は不完全なものになってしまいます!
ドーナツとコーヒーカップが同じであることを示すには、次のようにします。
さて、これらは互いに変形することができます。
私たちはこの2つの物体を「同相性」(ギリシャ語のhomoios=同一、morphe=形から)と呼びます。
ちょうどプラトン立体が球に同相であるように。
そしてあなたの体は鼻をつまんで閉じるとトーラスに同相になる。