(Există o altă „Formulă a lui Euler” despre numerele complexe,
această pagină este despre cea folosită în Geometrie și Grafice)
Formula lui Euler
Pentru orice poliedru care nu se intersectează, numărul
- numărul de fețe
- plus numărul de vârfuri (puncte de colț)
- minus numărul de muchii
este întotdeauna egal cu 2
Acesta se poate scrie: F + V – E = 2
 |
Încercați-o pe cub: Un cub are 6 fețe, 8 vârfuri și 12 muchii, deci: 6 + 8 – 12 = 2 |
Exemplu cu solidele platonice
Să încercăm cu cele 5 solide platonice:
| Numele | Fațe | Vârfuri | Vârfuri | F+V-.E | |||
|---|---|---|---|---|---|---|---|
| Tetraedru |  |
4 | 4 | 6 | 2 | ||
| Cub |  |
6 | 8 | 8 | 8 | 12 | 2 |
| Octaedru |  |
8 | 6 | 12 | 2 | ||
| Dodecaedru |  |
12 | 20 | 30 | 2 | ||
| Icosaedru |  |
20 | 12 | 30 | 30 | 2 |
(De fapt, formula lui Euler poate fi folosită pentru a demonstra că există doar 5 solide platonice)
|
De ce întotdeauna 2? 7 + 8 – 13 = 2 |
 |
|
Sau încercați să includeți un alt vârf, 6 + 9 – 13 = 2. |
 |
| „Indiferent ce facem, întotdeauna ajungem la 2” (Dar numai pentru acest tip de poliedru … citiți mai departe!) |
Sfera

Toate solidele platonice (și multe alte solide) sunt ca o sferă … le putem remodela astfel încât să devină o sferă (le mutăm punctele de colț, apoi le curbăm puțin fețele).
Din acest motiv știm că F + V – E = 2 pentru o sferă
(Atenție, nu putem spune pur și simplu că o sferă are 1 față și 0 vârfuri și muchii, pentru că F+V-E=1)
Deci, rezultatul este din nou 2.
Dar nu întotdeauna 2 … !
Acum că ați văzut cum funcționează, haideți să descoperim cum nu funcționează.
Ce s-ar întâmpla dacă am uni două colțuri opuse ale unui icosaedru?
Este tot un icosaedru (dar nu mai este convex).
De fapt, seamănă puțin cu o tobă unde cineva a cusut partea de sus și cea de jos.
Acum, există același număr de muchii și fețe … dar cu un vertex mai puțin!
Deci:
F + V – E = 1
Oh, nu! Nu se adună întotdeauna la 2.
Motivul pentru care nu a funcționat a fost că această nouă formă este practic diferită … acea bucățică alăturată din mijloc înseamnă că două vârfuri sunt reduse la 1.
Caracteristica lui Euler
Deci, F+V-E poate fi egal cu 2, sau 1, și poate și alte valori, așa că formula mai generală este
F + V – E = χ
Unde χ se numește „caracteristica lui Euler”.
Iată câteva exemple:
| Forma | χ | |
|---|---|---|
| Sferă |  |
2 |
| Torus |  |
0 |
| Fâșia lui Mobius | 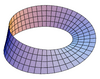 |
0 |

Și caracteristica lui Euler poate fi, de asemenea, mai mică decât zero.
Acesta este „Cubohemioctaedrul”: Are 10 fețe (poate părea mai multe, dar unele dintre fețele „interioare” sunt de fapt doar o singură față), 24 de muchii și 12 vârfuri, deci:
F + V – E = -2
De fapt, caracteristica Euler este o idee de bază în topologie (studiul naturii spațiului).
Gogoașă și ceașcă de cafea

(Animație prin amabilitatea
Wikipedia User:Kieff)
În sfârșit, această discuție ar fi incompletă dacă nu am arăta că o gogoașă și o ceașcă de cafea sunt într-adevăr același lucru!
Bine, ele pot fi deformate una în alta.
Spunem că cele două obiecte sunt „homeomorfe” (de la grecescul homoios = identic și morphe = formă)
La fel cum solidele platonice sunt homeomorfe la sferă.
Și corpul tău este homeomorf la un torus dacă îți strângi nasul.