(Van egy másik “Euler-képlet” is a komplex számokról,
ez az oldal a Geometria és grafikonok témakörben használt képletről szól)
Euler-képlet
Minden olyan poliéderre, amely nem metszi önmagát, az
- Felületek száma
- plusz a csúcsok (sarokpontok) száma
- mínusz az élek száma
mindig egyenlő 2
Ez leírható: F + V – E = 2
 |
Kipróbáljuk a kockán: A kockának 6 oldala, 8 csúcsa és 12 éle van, tehát: 6 + 8 – 12 = 2 |
Példa a platóni szilárd testekkel
Próbáljuk meg az 5 platóni szilárd testtel:
| Név | Felületek | Sarkok | Eszögek | F+V-E | |
|---|---|---|---|---|---|
| Tetraéder |  |
4 | 4 | 6 | 2 |
| Kocka |  |
6 | 8 | 12 | 2 |
| Oktaéder |  |
8 | 6 | 12 | 2 |
| Dodekaéder |  |
12 | 20 | 30 | 2 |
| Ikozaéder |  |
20 | 12 | 30 | 2 |
(Valójában Euler képletével bizonyítható, hogy csak 5 platóni szilárd test létezik)
|
Miért mindig 2? 7 + 8 – 13 = 2 |
 |
|
|
Vagy próbáljunk meg felvenni egy másik csúcsot, 6 + 9 – 13 = 2. |
 |
|
| “Mindegy mit csinálunk, mindig 2 lesz a végeredmény” (De csak az ilyen típusú poliédereknél … olvass tovább!) |
A Gömb

Minden platóni szilárd test (és sok más szilárd test) olyan, mint egy Gömb … átformálhatjuk őket úgy, hogy Gömbbé váljanak (áthelyezzük a sarokpontjaikat, majd egy kicsit meggörbítjük az arcukat).
Ezért tudjuk, hogy egy gömb esetében F + V – E = 2
(Vigyázat, nem mondhatjuk egyszerűen, hogy egy gömbnek 1 arca van, és 0 csúcsa és éle, mert F+V-E=1)
Az eredmény tehát ismét 2.
De nem mindig 2 … !
Most, hogy látod, hogyan működik, fedezzük fel, hogyan nem működik.
Mi lenne, ha egy ikozaéder két ellentétes sarkát összekötnénk?
Ez még mindig egy ikozaéder (de már nem domború).
Valójában egy kicsit úgy néz ki, mint egy dob, aminek valaki összefűzte a tetejét és az alját.
Most, ugyanannyi él és felület van … de egy csúcsponttal kevesebb!
Szóval:
F + V – E = 1
Oh nem! Ez nem mindig adódik össze 2-re.
Azért nem működött, mert ez az új alakzat alapvetően más … az összekötött rész középen azt jelenti, hogy két csúcspontot csökkentünk 1-re.
Euler-karakterisztika
Az F+V-E tehát lehet 2, vagy 1, és esetleg más értékek, így az általánosabb képlet
F + V – E = χ
Ahol χ az úgynevezett “Euler-karakterisztika”.
Itt van néhány példa:
| alak | χ | |
|---|---|---|
| Gömb |  |
2 |
| Torusz |  |
0 |
| Mobius szalag | 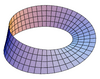 |
0 |

És az Euler-karakterisztika is lehet nullánál kisebb.
Ez a “kubohémioktaéder”: Ennek 10 oldala van (többnek tűnhet, de néhány “belső” oldala valójában csak egy oldal), 24 éle és 12 csúcsa, tehát:
F + V – E = -2
Az Euler-karakterisztika valójában a topológia (a tér természetének tanulmányozása) egyik alapgondolata.
Fánk és kávéscsésze

(Animáció a
Wikipedia User:Kieff jóvoltából)
Végül ez a beszélgetés nem lenne teljes anélkül, hogy megmutatnánk, hogy a fánk és a kávéscsésze valóban ugyanaz!
Nos, deformálhatók egymásba.
Azt mondjuk, hogy a két tárgy “homeomorf” (a görög homoios = azonos és morphe = alak)
Mint ahogy a platóni szilárd testek is homeomorfok a gömbhöz.
És a tested is homeomorf egy tóruszhoz, ha összeszorítod az orrodat.