(Der findes en anden “Eulers formel” om komplekse tal,
denne side handler om den, der bruges i Geometri og grafer)
Eulers formel
For ethvert polyeder, der ikke skærer sig selv, er
- antallet af flader
- plus antallet af hjørner (hjørnepunkter)
- minus antallet af kanter
altid lig med 2
Dette kan skrives: F + V – E = 2
 |
Prøv det på terningen: En terning har 6 flader, 8 hjørner og 12 kanter, så: 6 + 8 – 12 = 2 |
Eksempel med platoniske søjler
Lad os prøve med de 5 platoniske søjler:
| Navn | Flader | Skråninger | Ekanter | F+V-E | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tetraeder |  |
4 | 4 | 6 | 6 | 2 | ||||
| Kube |  |
6 | 8 | 12 | 2 | |||||
| Oktaeder |  |
8 | 6 | 12 | 2 | |||||
| Dodekaeder |  |
12 | 20 | 30 | 2 | |||||
| Icosaeder |  |
20 | 12 | 30 | 30 |  |
20 | 12 | 30 | 2 |
(Faktisk kan Eulers formel bruges til at bevise, at der kun findes 5 platoniske legemer)
|
Hvorfor altid 2? 7 + 8 – 13 = 2 |
 |
|
Og prøv at medtage endnu et toppunkt, 6 + 9 – 13 = 2. |
 |
| “Uanset hvad vi gør, ender vi altid med 2” (Men kun for denne type polyeder … læs videre!) |
Kuglen

Alle platoniske faste legemer (og mange andre faste legemer) er som en kugle … vi kan omforme dem, så de bliver til en kugle (flyt deres hjørnepunkter, og krum derefter deres flader lidt).
Derfor ved vi, at F + V – E = 2 for en kugle
(Pas på, vi kan ikke bare sige, at en kugle har 1 flade, og 0 hjørner og kanter, for F+V-E=1)
Så resultatet er 2 igen.
Men ikke altid 2 … !
Nu da du har set, hvordan det virker, skal vi opdage, hvordan det ikke virker.
Hvad nu, hvis vi sammenføjede to modsatte hjørner af et isosaeder?
Det er stadig et isosaeder (men ikke længere konvekse).
Det ligner faktisk lidt en tromle, hvor nogen har syet top og bund sammen.
Nu er der det samme antal kanter og flader … men et toppunkt mindre!
Så:
F + V – E = 1
Oh nej! Det går ikke altid op til 2.
Grunden til at det ikke virkede var, at denne nye form er grundlæggende anderledes … den sammenføjede bit i midten betyder, at to hjørner bliver reduceret til 1.
Eulerkarakteristik
Så F+V-E kan være lig med 2, eller 1, og måske andre værdier, så den mere generelle formel er
F + V – E = χ
Hvor χ kaldes “Eulerkarakteristik”.
Her er et par eksempler:
| Form | χ | ||
|---|---|---|---|
| Sfære |  |
2 | |
| Torus |  |
0 | |
| Mobius Strip | 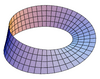 |
0 |

Og Eulerkarakteristikken kan også være mindre end nul.
Dette er “kubohemioktaederet”: Det har 10 flader (det ser måske ud til at være flere, men nogle af de “indre” flader er i virkeligheden kun én flade), 24 kanter og 12 hjørner, så:
F + V – E = -2
Den Eulerske karakteristik er faktisk en grundlæggende idé i topologi (studiet af rummets natur).
Donut og kaffekop

(Animation courtesy
Wikipedia User:Kieff)
Sidst ville denne diskussion være ufuldstændig uden at vise, at en Donut og en kaffekop i virkeligheden er det samme!
Jamen, de kan deformes til hinanden.
Vi siger, at de to objekter er “homeomorfe” (fra græsk homoios = identisk og morphe = form)
Sådan som de platoniske faste legemer er homeomorfe til kuglen.
Og din krop er homeomorfe til en torus, hvis du kniber din næse sammen.