Eulerův vzorec

(Existuje ještě jeden „Eulerův vzorec“ o komplexních číslech,
tato stránka je o tom, který se používá v Geometrii a grafech)

Pro každý mnohostěn, který se neprotíná, se

počet stěn
plus počet vrcholů (rohových bodů)
minus počet hran

vždy rovná 2

To lze zapsat: F + V – E = 2

Zkuste to na krychli:

Kostka má 6 stěn, 8 vrcholů a 12 hran,

takže:

6 + 8 – 12 = 2

Příklad s platónskými tělesy

Zkusíme to s 5 platónskými tělesy:

Název	Plochy	Vrcholy	Hrany	F+V-E
Tetraedr	4	4	6	2
Krychle	6	8	12	2
Oktaedr	8	6	12	2
Dodekaedr	12	20	30	2
Ikosaedr	20	12	30	2

(Ve skutečnosti lze pomocí Eulerova vzorce dokázat, že existuje pouze 5 platónských těles)

Proč vždy 2? Představte si, že vezmete krychli a přidáte hranu (z rohu do rohu jedné stěny). Získáme hranu navíc a navíc jednu stěnu navíc: 7 + 8 – 13 = 2

Nebo zkusíme přidat další vrchol, a dostaneme hranu navíc: 6 + 9 – 13 = 2.
„Ať děláme, co děláme, vždycky nám vyjde 2“ (Ale jen pro tento typ mnohostěnu … čtěte dál!)

Koule

Všechna platónská tělesa (a mnoho dalších těles) jsou jako koule … můžeme je přetvořit tak, aby se z nich stala koule (posuneme jejich rohové body, pak trochu zakřivíme jejich stěny).

Z tohoto důvodu víme, že F + V – E = 2 pro kouli

(Pozor, nemůžeme jednoduše říci, že koule má 1 stěnu a 0 vrcholů a hran, neboť F+V-E=1)

Takže výsledek je opět 2.

Ale ne vždy 2 … !

Teď, když vidíte, jak to funguje, objevíme, jak to nefunguje.

Co kdybychom spojili dva protilehlé rohy ikosaedru?

Stále je to ikosaedr (ale už není konvexní).

V podstatě vypadá trochu jako buben, na kterém někdo sešil horní a dolní část.

Teď je tam stejný počet hran a stěn… ale o jeden vrchol méně!

Takže:

F + V – E = 1

Ale ne! Vždycky se to nesčítá do 2.

Důvod, proč to nefungovalo, byl ten, že tenhle nový tvar je v podstatě jiný … ten spojený kousek uprostřed znamená, že se dva vrcholy zmenší na 1.

Takže to nefungovalo.

Eulerova charakteristika

Takže F+V-E se může rovnat 2, nebo 1, a možná i jiným hodnotám, takže obecnější vzorec je

F + V – E = χ

Kde χ se nazývá „Eulerova charakteristika“.

Tady je několik příkladů:

Tvar		χ
Sféra		2
Torus		0
Mobiusův pás		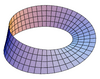0

A Eulerova charakteristika může být také menší než nula.

To je „kubohemioktaedr“: Má 10 stěn (může to vypadat jako více, ale některé „vnitřní“ stěny jsou ve skutečnosti jen jednou stěnou), 24 hran a 12 vrcholů, takže:

F + V – E = -2

Ve skutečnosti je Eulerova charakteristika základní myšlenkou v topologii (nauka o povaze prostoru).

Donut a šálek kávy

(Animace s laskavým svolením
Wikipedia User:Kieff)

Nakonec by tato diskuse nebyla úplná, kdybychom neukázali, že Donut a šálek kávy jsou opravdu totéž!

No, dají se deformovat jeden do druhého.

Říkáme, že tyto dva objekty jsou „homeomorfní“ (z řeckého homoios = stejný a morphe = tvar)

Stejně jako platónská tělesa jsou homeomorfní ke kouli.

A vaše tělo je homeomorfní k torusu, když si sevřete nos.

Podle toho, co říkáte, je vaše tělo homeomorfní k torusu.