(Det finns en annan ”Eulers formel” om komplexa tal,
denna sida handlar om den som används i geometri och grafer)
Eulers formel
För varje polyeder som inte skär sig själv, är
- antalet sidor
- plus antalet hörn (hörnpunkter)
- minus antalet kanter
alltid lika med 2
Detta kan skrivas: F + V – E = 2
 |
Prova det på kuben: En kub har 6 sidor, 8 hörn och 12 kanter, så: 6 + 8 – 12 = 2 |
Exempel med de platonska soliderna
Låt oss prova med de fem platonska soliderna:
| Namn | Figurer | Växter | Sidor | Eggar | F+V-E | |
|---|---|---|---|---|---|---|
| Tetraeder |  |
4 | 4 | 6 | 2 | |
| Kubus |  |
6 | 8 | 12 | 2 | |
| Oktaeder |  |
8 | 6 | 12 | 2 | |
| Dodekaeder |  |
12 | 20 | 30 | 2 | |
| Icosaeder |  |
20 | 12 | 30 | 30 | 2 |
(Eulers formel kan faktiskt användas för att bevisa att det bara finns 5 platonska solider)
|
Varför alltid 2? 7 + 8 – 13 = 2 |
 |
|
Och försök att inkludera ytterligare en spets, 6 + 9 – 13 = 2. |
 |
| ”Oavsett vad vi gör får vi alltid 2” (Men bara för den här typen av polyeder … läs vidare!) |
Sfären

Alla platonska solider (och många andra solider) är som en sfär … vi kan omforma dem så att de blir en sfär (flytta deras hörnpunkter, böj sedan deras ytor lite).
För denna anledning vet vi att F + V – E = 2 för en sfär
(Var försiktig, vi kan inte bara säga att en sfär har 1 yta, och 0 hörn och kanter, för F + V – E = 1)
Så, resultatet är 2 igen.
Men inte alltid 2 … !
Nu när du har sett hur detta fungerar, ska vi upptäcka hur det inte fungerar.
Hur skulle det vara om vi sammanfogade två motsatta hörn på en isosaeder?
Det är fortfarande en isosaeder (men inte längre konvex).
Det ser faktiskt lite ut som en trumma där någon har sytt ihop över- och undersida.
Nu finns det samma antal kanter och ytor … men ett hörn mindre!
Så:
F + V – E = 1
Oh nej! Det går inte alltid att addera till 2.
Anledningen till att det inte fungerade var att den här nya formen är i grunden annorlunda … den sammanfogade biten i mitten innebär att två hörn reduceras till 1.
Eulerkarakteristik
F+V-E kan alltså vara lika med 2, eller 1, och kanske andra värden, så den mer allmänna formeln är
F + V – E = χ
Varvid χ kallas ”Eulerkarakteristik”.
Här är några exempel:
| Form | χ | |
|---|---|---|
| Sfär |  |
2 |
| Torus |  |
0 |
| Mobius Strip | 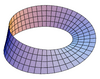 |
0 |

Och Eulers karakteristik kan också vara mindre än noll.
Detta är ”kubohemioktaedern”: Den har 10 ytor (det kan se ut som fler, men vissa av de ”inre” ytorna är egentligen bara en yta), 24 kanter och 12 hörn, så:
F + V – E = -2
Förresten är Eulers karakteristik en grundläggande idé inom topologin (studiet av rummets natur).
Donut och kaffekopp

(Animation courtesy
Wikipedia User:Kieff)
Sluttligen skulle den här diskussionen vara ofullständig utan att visa att en donut och en kaffekopp egentligen är samma sak!
Ja, de kan deformeras till varandra.
Vi säger att de två objekten är ”homeomorfa” (från grekiskans homoios = identisk och morphe = form)
Såsom de platoniska soliderna är homeomorfa till sfären.
Och din kropp är homeomorf till en torus om du kniper ihop näsan.